一种基于分支过程的信息流行度动力学模型*

吴联仁 李瑾颉 齐佳音3)

1) (上海对外经贸大学工商管理学院, 上海 201620)

2) (上海师范大学数理学院, 上海 200234)

3) (北京邮电大学, 可信分布式计算与服务教育部重点实验室, 北京 100876)

1 引 言

社交媒体上的信息流行度演化与预测给复杂系统的研究者提出了诸多挑战, 如识别“病毒式”传播的原因、网络结构特征以及通过信息的内容和早期的关注预测未来的流行度. 虽然在线信息流行度的建模与预测已经取得了一定的研究进展[1−4], 然而这个方向的研究大多由于可用的大规模数据缺少而受到阻碍. 近年来, 从在线社交网络获得的大规模社交数据为探索人类行为特征及其对在线内容流行的影响创造了前所未有的机会.

建模和预测信息流行度的困难在于各种混杂因素的共存[5−9]. 同时, 它给研究人员带来了许多挑战, 包括原因的识别[10−13], 时间效应[14]和结构特征[15,16]. 一些学者对这一问题提出了不同的看法. Cetin和Bingol[17]认为个人注意力对信息的流行有重要影响, 并且提出能见度的衰退和分散注意力的结合解释了为什么社交网络中的大多数信息级联不能成为流行. Weng等[18]采用agent−based模型来研究模因(memes)之间的竞争是否会影响其流行度, 结果表明模因的流行度存在异质性, 这种现象是由模因竞争用户有限的注意力和在线网络的结构共同导致的. Gleeson等[19]认为, 有限的用户注意力资源限制了消息的流行, 并且自然地导致一些消息变得非常流行, 其他消息只是中等流行, 或者被忽略. Yan等[20,21]通过微博信息数据从人类动力学方面研究微博信息传播及扩散.

针对上述问题, 本文对新浪微博的信息数据和网络结构数据进行了分析, 结果发现信息流行度衰减遵循标度律. 其次, 提出了基于分支过程的概率模型, 来描述微博信息流行度变化的过程. 第三,对所提出的模型进行数值仿真和理论求解, 发现该模型能够再现真实社交网络数据的若干特征. 此外, 信息流行度分布的幂指数与微博网络的度分布幂指数相关, 微博系统中信息流行度受网络结构的影响.

2 模型描述

在线社交网络用户之间相互关注形成有向网络(如Twitter、新浪微博等). 在新浪微博系统中,每个用户具有“微博首页”和“个人页面”两个列表.用户关注的好友如果发出信息, 这些信息按时间先后顺序都将显示在“微博首页”这个列表上. 当用户打开微博系统查看“微博首页”列表上的信息时, 就会对感兴趣的微博进行转发或评论. 转发的微博信息同时会显示在“个人页面”这个列表上. 本文定义表示微博信息的流行度, 即从信息被生成后时间内获得转发和评论的总数.表示在时间信息获得流动度的概率.

由于“微博首页”存储列表的顶部是最新收到的信息, 之前收到的信息会逐渐淹没在列表的底部. 根据用户注意力有限的假设, 每次用户从“微博首页”列表顶部开始查看信息, 并且查看的信息是有限的. 这就会导致一些被淹没在列表底部的信息不被用户评论或转发. 不失一般性, 此处假设“微博首页”和“个人首页”存储信息的能力为1, 即都只能保存一条信息, 新的信息到来时将覆盖掉原来保存在列表上的信息.

图1描述的是微博系统中信息传播的过程. 对于每个用户在当前时刻有两个动作(或状态)：1)以概率生成一条新的信息发出去; 2)以概率转发“微博列表”上已有的信息. 如用户1在时刻以概率生成了一条信息(用圆圈表示), 同时发给其粉丝用户2和3; 在时刻用户2以概率转发这条信息给其粉丝用户4和5; 在时刻, 用户3又以概率生成一条新的信息(用方框表示), 并将该信息发给其粉丝用户6和7. 每当信息被传播一次, 信息的流行度加1.

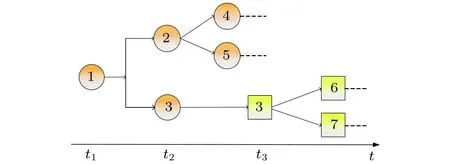
图1 流行度模型示意图Fig. 1. Schematic of the model.

3 模型方程与求解

根据第2节的模型描述, 本节采用分支过程来刻画信息的流行度动力学过程, 微博系统中每条消息的传播都遵循一个分支过程.

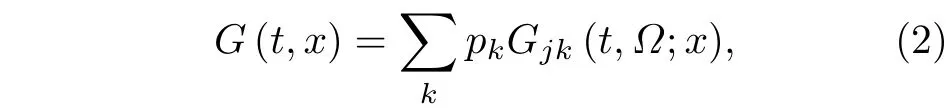
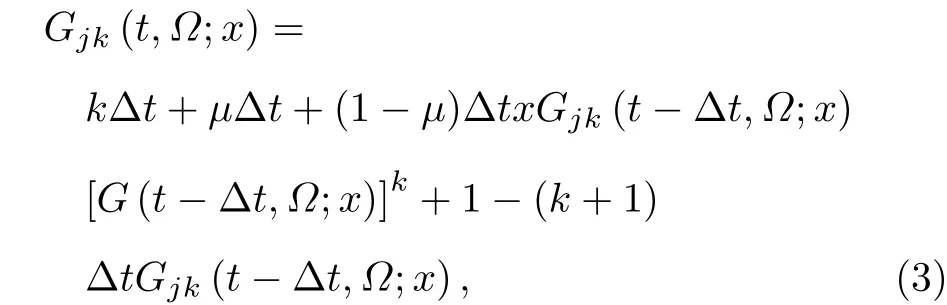
表1 一个时间步节点(用户)“微博首页”的结果Table 1. Single time−step outcomes of user’s list.

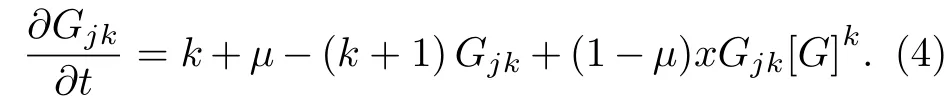
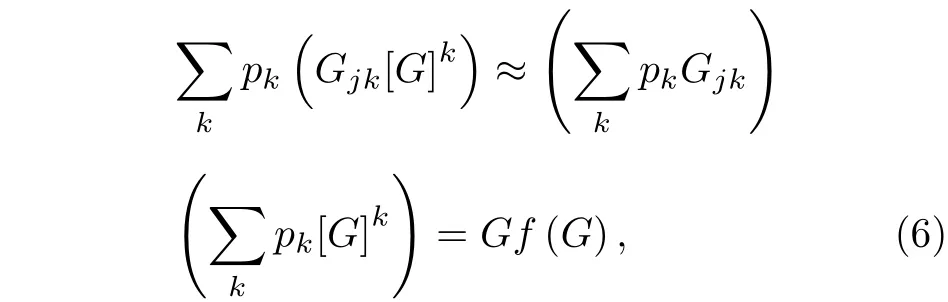
则(5)式变为

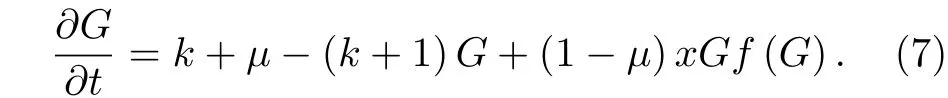
将上面的推导一般化为每个用户的列表具有容量c, 即用户的“微博首页”和“个人页面”可同时保存c条微博信息：

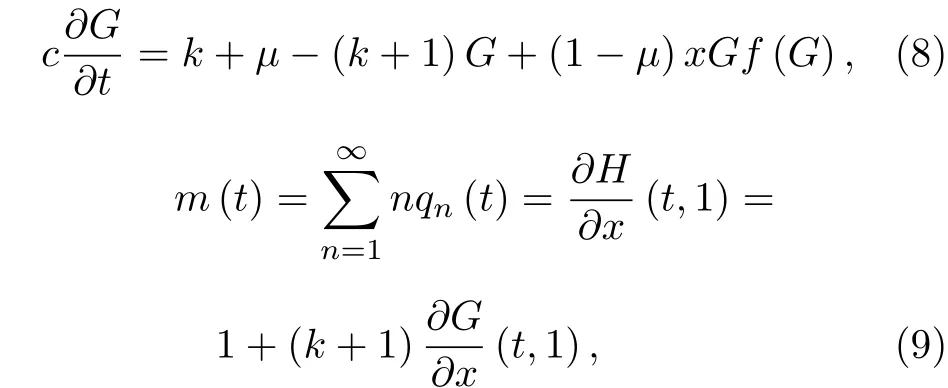
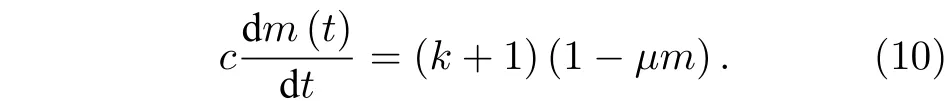
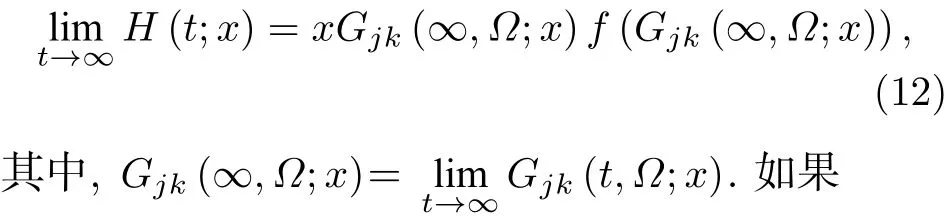
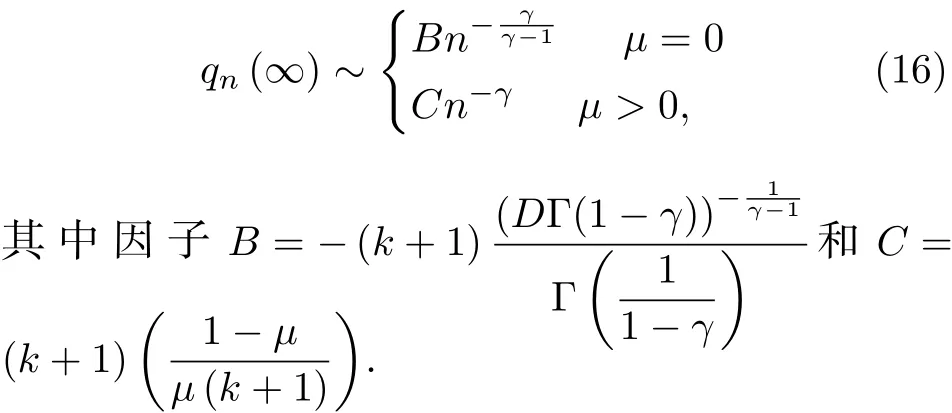
4 实证分析和数值模拟

4.1 数据描述和处理

本文分析了两个数据集, 均通过新浪微博开放平台API收集(www.weibo.com), 新浪微博是目前中国最流行的微博平台之一. 第1个数据集是微博信息数据, 通过滚雪球采样的方法收集了某个话题在2009/8/20―2010/9/3之间发布的125139条微博, 以及这些微博被转发了2260826次和1822450条评论. 每条微博包括发出用户ID、微博ID、微博发布时间、微博内容、转发次数和评论次数. 此外还采集了微博的评论时间, 微博的转发时间虽无法获得, 但微博的转发流行度分布和评论流行度分布具有相同的分布特征(如图2所示), 均服从幂指数约为1.8的幂律分布. 因此, 评论流行度的变化可近似表示微博整体流行度的变化(评论流行度和转发流行度).

第2个数据是微博用户数据, 第2个数据集收集了参与话题讨论的41667个用户信息. 对每个用户, 采集了用户ID、用户关注数和关注关系、用户粉丝数. 从而获得微博网络用户度分布情况, 数据统计分析发现用户入度(粉丝)和出度(关注)分布均服从幂指数约为1.5的幂律分布(如图3所示),但出度分布在2000附近具有一个截断, 这是由于新浪微博系统初期允许关注的上限是2000.

图2 微博的流行度分布Fig. 2. Distribution of micro−blogs popularity.

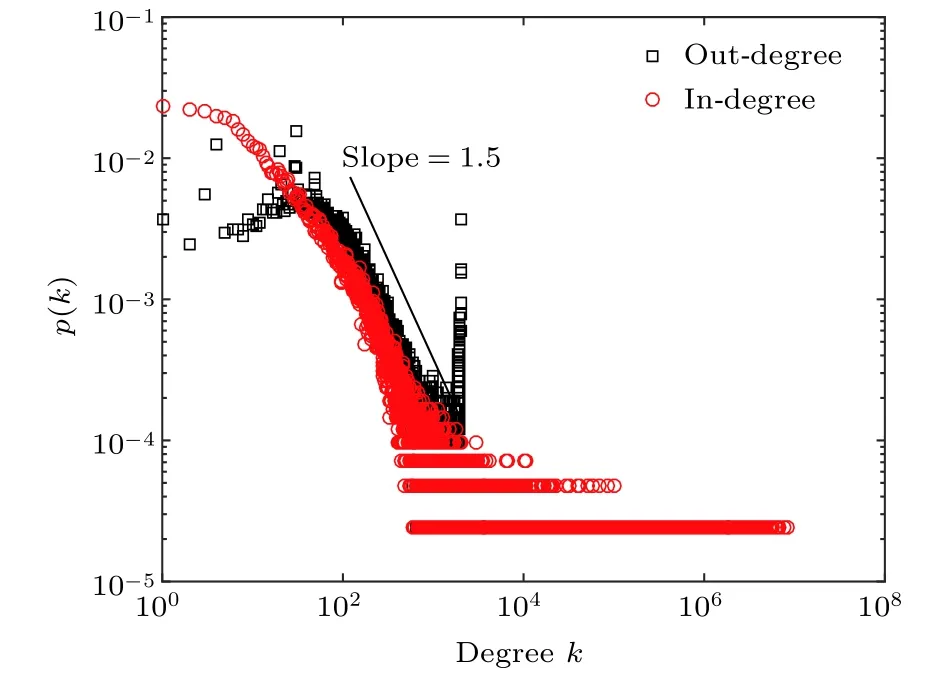
图3 微博用户度分布Fig. 3. Distribution of out−degree and in−degree.

4.2 数值模拟

为了验证分支过程近似的精确性, 并探讨网络结构与有限注意力的相互作用, 本文将模型的数值仿真结果与实际数据和理论预测结果进行比较. 首先生成具有指定度分布的有向网络, 网络的度分布服从幂律分布,. 模型参数设定为节点总数是, 且

数值仿真的微博信息的平均流行度(蓝圆线),与实际数据(黑钻石线)和方程6的理论预测(红方线)的比较如图4所示. 其中参数取值为微博生成概率, 平均入度, 微博列表存储信息能力. 因新浪微博网络中不同时间窗口、不同主题话题下微博信息流行度存在差异, 本文实证数据计算结果与理论模拟存在偏差. 从图4可见, 在初始阶段, 平均流行度的实际数据与理论预测和仿真偏差较大, 随着时间不断增加, 偏差先减小后增大, 最后实际平均流行度值和理论预测值均趋向于定值, 偏差稳定. 另外在数据处理与选择时, 单个微博信息流行度时间序列数据点大于等于10时, 该微博信息才被纳入计算平均流行度的数据. 每个微博信息流行度的时间序列数据点不相等, 也导致了平均流行度的计算结果和理论模拟的偏差.

图4 微博信息平均流行度Fig. 4. Mean popularity of Micro−blogs.

图5 比较了微博信息流行度模型仿真结果、实际数据和理论预测的结果. 其中参数取为,. 网络结构是新浪微博中41667个用户数据生成的网络. 在较小时, 模型仿真结果与实际数据及理论预测结果一致, 当时, 实证数据与仿真结果和理论预测之间存在一定偏差, 但大致结果是符合的. 导致偏差的主要原因是, 基于分支过程的流行度模型是建立在假设微博网络是树形结构基础上的, 但实际上, 新浪微博41667用户生成的网络中34%的链接是互惠链接. 基于树形结构理论的精确结果应用于现实世界的网络中, 因此导致了一定的偏差.

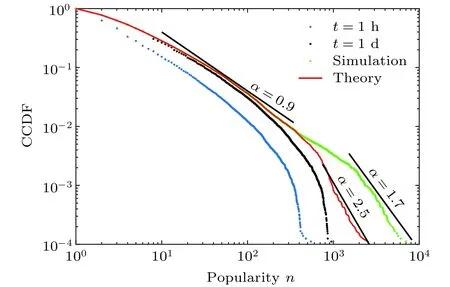
图5 微博信息流行度的互补累积概率分布(CCDF)Fig. 5. Complementary cumulative distribution functions(CCDFs)–the fraction of micro−blogs with popularity .

通过对微博信息评论转发数据和网络结构数据的统计分析可知, 在微博系统中存在高度的异质性, 如流行度小于100的微博信息占比达到95.8%, 而流动度超过1万的微博信息数量是非常少的. 粉丝数(入度)小于100的用户占比达56.4%,而有的用户粉丝数高达百万. 通过仿真, 重现了复杂社会系统中的高度异质性, 大量的流行度(或关注)都被少量的信息(或用户)获得, 得到了流行度依赖时间的重尾分布特征. 本文所提出的框架构成了社会传播现象的零模型, 与纯粹的实证研究或基于模拟的模型相比, 它清楚地区分了影响信息流行度的两个不同因素的作用, 即用户的记忆时间和社交网络的连接结构.

5 总结与讨论

在线社交媒体极大地影响了人们彼此沟通的方式. 近年来, 在线社交媒体信息流行度的预测和建模引起了众多学者的关注. 例如, 预测和建模社交媒体上的新闻流行度[22]和量化论文流行度[23].本文引入并分析了一种信息传播的概率模型, 该模型具有分析易处理性, 可以再现实际数据的若干特征. 但是该模型也存在一定的局限性, 其中要求做出一些假设以获得分析结果. 在将来的研究中, 我们希望对模型进行一些可能的扩展.