区块链的椭圆曲线密码算法侧信道安全分析

万武南，陈 豪，陈 俊，张仕斌

1.成都信息工程大学网络空间安全学院，成都610225

2.成都信息工程大学计算机学院，成都610225

2008年,中本聪首次提出区块链（blockchain）的概念[1],区块链技术最早作为比特币和密码货币的底层技术逐渐引起了产业界与学术界的广泛关注.2016年，《中国区块链技术和应用发展白皮书》[2]将区块链定义为：分布式存储、点对点传输、共识机制、密码技术等计算机技术应用的新型模式，具有去中心化、去信任、匿名、数据不可篡改等安全特性，已在电子商务、数字医疗、数字防伪等许多领域得到广泛应用[3-4].

随着区块链技术的发展，区块链数据网络节点数据中心面临着越来越大的数据量和工作量复杂性要求，为了解决区块链中共识机制的效率瓶颈问题[5-6]，区块链中密码技术、共识机制采用硬件实现，在低能源成本下提高系统的性能.如各芯片厂商先后推出多款比特币芯片、比特币“挖矿机”芯片等硬件设备.

但自文献[7]提出的差分功耗分析（differential power analysis,DPA）[7]方法以来，简单功耗分析（simple power analysis,SPA）[8]、DPA[9-10]、相关功耗分析（correlation power analysis,CPA）[11]等方法先后被提出.研究者针对AES、DES、RSA、ECC等密码算法硬件设备的侧信道攻击方法层出不穷[12]，区块链硬件设备将面临侧信道攻击.目前，区块链应用系统中推荐采用ECC密码算法.针对ECC算法的侧信道研究以椭圆曲线标量乘的侧信息攻击和防御为主[13-19]，如文献[14]针对ECDSA算法提出了模板攻击，随后研究人员提出了防御措施.文献[16-17]针对椭圆曲线多倍点计算过程进行攻击，并给出了防御措施.文献[19]提出了标量乘的选择明文的SPA攻击，并针对提出攻击方法提出了明文掩码的防御方法.

目前，椭圆曲线标量乘SPA攻击研究中，以标量乘倍点和倍加操作单位进行建模分析，而缺乏对标量乘倍点和倍加内部实现原子操作的功耗特征进行分析，以至于大部分防御方案从倍点和倍加层着手防御[20-21].本文详细分析了椭圆曲线标量乘的倍点和倍加内部运算步骤，给出了倍点和倍加原子操作运算的功耗特征模型，然后根据功耗特性模型中倍点和倍加产生的明显功耗差别，通过一条功耗曲线就可以获取密钥信息.最后从标量乘的倍点和倍加运算原子操作的不同造成功耗差异入手，给出原子操作级别的等功耗防御方案，为区块链硬件设备提出防御侧信道攻击的ECC密码算法，从而避免遭受侧信道攻击带来的安全威胁.

1 预备知识

1.1 区块链密码技术

区块链是一种源于数字加密货币比特币的分布式总账技术，根据参与方式不同，总体可分为公有链、联盟链、私有链3种类型.区块链中每个区块包括区块头和区块体两大部分，由唯一哈希值作为区块地址与之对应，后一个区块记录前一个区块的哈希值，从而将每一个区块连接形成链式结构，其结构如图1所示.区块链中的每笔交易由一组“输入”和“输出”列表组成.交易的“输入”则包含由交易方对交易进行数字签名的数据，保证交易数据不可篡改和伪造.数字签名在区块链交易中主要应用过程如图2所示[13].交易用户用私钥进行签名，形成新的交易，然后用户对该交易广播到区块链系统，系统其他节点可以使用交易用户的公钥进行验证.

目前，在比特币系统中，签名算法推荐使用ECC系列算法[4].若ECC遭遇攻击，私钥会被破解，这将给区块链系统带来巨大安全威胁.例如，在比特币系统中，丢失私钥就意味着丢失了对应地址的全部比特币资产.因此，选择安全的ECC算法是保证区块链安全的基础.ECC签名算法的安全性主要依赖于大整数离散对数困难问题，但易于遭受侧信道攻击.

图1 区块链数据结构Figure 1 Data structure of blockchain

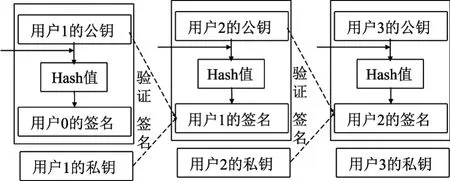
图2 交易签名过程Figure 2 Transaction signature procedure

1.2 椭圆曲线密码体制

ECC签名算法最常用是ECDSA，签名过程如算法1[10].

算法1 ECDSA签名算法

输入D=(q,P,n,Curve),private keyd,messagem

输出Signature(r,s)

①选择随机数k,1≤k≤n

②计算[k]P=(x1,y1),where 0≤x1≤q-1

③计算r=x1modn.ifr=0,then go to step①

④计算e=H(m)

⑤计算s=k-1(e+dr)modn.ifs=0 then go to step①.

⑥返回签名(r,s)

根据算法1可知，若签名计算过程中随机数k能够被破译，已知签名(r,s),可以通过式(1)和(2)计算出私钥d.

算法2用二进制NAF的标量乘

输入正整数k，P∈E(Fq)

输出[k]P

②设置Q←∞

③fori=l-1 to 0

3.父母管教意见不统一或严重的溺爱，是普遍的诱因。家庭成员关爱和教育孩子的出发点不一致，在许多具体问题的处理上监护人意见不统一，使孩子感到无所适从。这种充满矛盾的家庭环境造成学生矛盾的心理，影响孩子的认知和学习行为。

Q=2Q

若ki=1，则Q=Q+P

若ki=-1，则Q=Q-P

④返回Q

1.3 标量乘倍点和倍加的实现

椭圆曲线标量乘倍点和倍加运算过程与所选择坐标系相关，仿射坐标下的椭圆曲线包含无穷远点，实现较为不便，并且倍点和倍加运算需要进行求逆运算，而求逆运算要比乘法运算耗时，因此一般选择标准重影坐标系、雅克比坐标系、雅克比-仿射坐标系[21].在各坐标系下，倍点和倍加运算如算法3所示[14].

算法3 倍点和倍加实现算法

2 椭圆曲线标量SPA攻击和防御

2.1 标量乘倍点和倍加原子级操作的功耗模型

在真实环境下，密码算法运行的功耗曲线采集会受到设备、环境等多方面的影响，算法产生具体的功耗的组成为

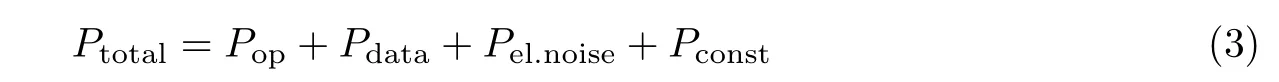
式中，Ptotal为总功耗，Pop为操作依赖分量，Pdata为数据依赖分量，Pel.noise为电子噪声，Pconst为恒定分量.

根据算法3可知，标量乘倍点和倍加的原子级操作主要包括大整数的模乘、模加、模减、移位、数据读取.每一种算法都将大整数乘法分解为若干次小整数的运算.理论上来说，每种原子级操作不一样，Pop特征不一样.由汉明重量功耗模型可知，数据操作位跳变越多，功耗区别越大.根据Pop功耗特性，模乘的功耗最大，数据读取操作的功耗最小.因此标量乘的原子操作功耗可以分为PHigh、PMedium、PLow3类，如图3所示.

模乘、模加、模减、移位、数据读取等操作功耗分别记为：模乘Pop_mod_mul(a,b)、模加Pop_mod_add(a,b)、模减Pop_mod_sub(a,b)、移位Pop_shift(a)、数据读取Pop_rw(a).则每种原子操作的功耗特性分类如表1所示.

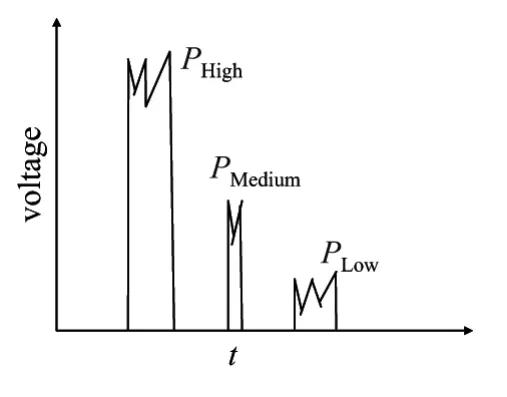
图3 不同操作功耗特征Figure 3 Power consumption characteristics of different arithmetic operations

表1 不同运算操作功耗特性Table 1 Power consumption characteristics of different arithmetic operations

根据算法3可知，倍点共有19步原子操作：8次模乘、9次模移位、2次模加、3次模减.而倍加的原子操作则为21步：13次模乘、5次模减，1次模移位，1次模加.椭圆曲线倍减Q=Q-P则可以看做是倍加运算，加数为-P=(x1,-y1)，因此倍点和倍加（倍减）的操作依赖主要功耗可以如下计算：

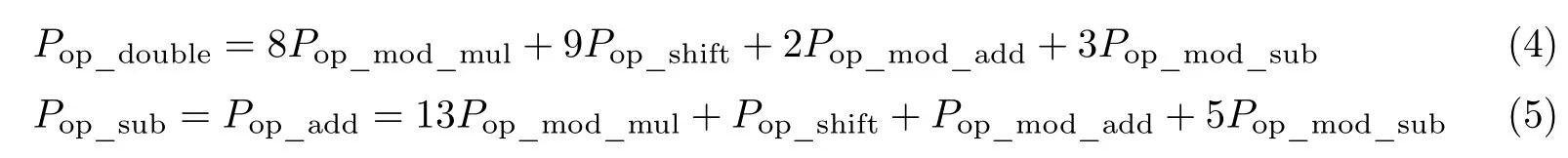
根据各操作的功耗特性不同，倍点操作功耗特性为8个PHigh和14个PMedium构成，而倍加运算则由13个PHigh和7个PMedium构成，倍点和倍加操作差异导致Pop功耗差异大，从而使得Ptotal的功耗差异大.并且而PHigh功耗与模乘运算具有一一对应的映射关系，模乘原子操作次数不同，使得模乘的PHigh功耗易于区分，因此可以通过PHigh出现次数区分倍点和倍加.另外不同操作运行的时间也存在差异，而倍点和倍加运算，核心操作运算的次数存在明显差异，两运算在时间上也存在差异.

2.2 标量乘功耗曲线特征分析和提取

采集椭圆曲线密码算法功耗曲线，如图4所示.与2.1节理论分析一致，标量乘的PHigh、PMedium、PLow3种功耗特征明显.根据对应数据读取等相关操作功耗PLow功耗特性，可以对功耗曲线分段，记为Segi，每一段则对应的标量乘算法2中第③步中倍点、倍加、倍减中一种运算.

根据2.1节理论分析，倍点与倍加（倍减）运算的功耗区分，可以通过每一段Segi曲线中倍点PHigh功耗特性：若某分段具有8个PHigh的功耗特性，则可以判断此分段是倍点运算产生的功耗；若分段具有13个PHigh的功耗特性，则可以判断此分段是倍加（倍减）产生的功耗.此外倍点功耗比倍加（倍减）功耗耗时要长的功耗特性，倍点共有22个操作运算，而倍加（倍减）则共有20个操作运算，如图4所示.

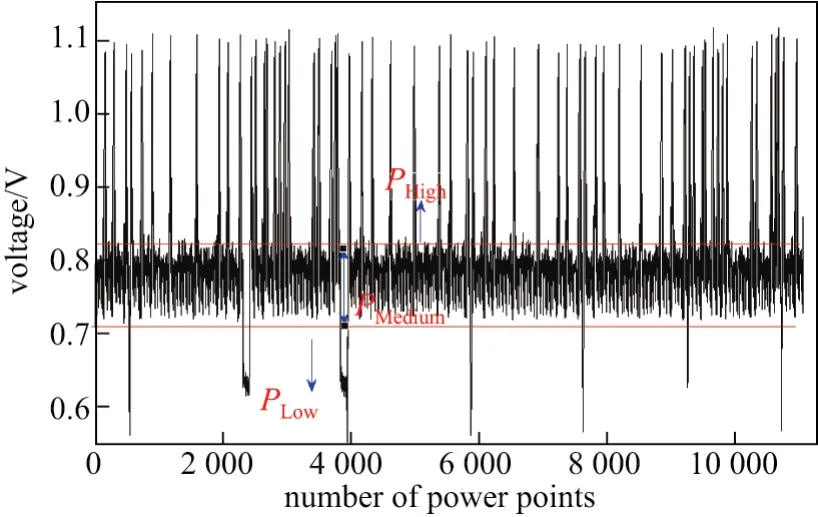
图4 标量乘功耗消耗特征Figure 4 Power consumption characteristics of scalar multiplication

某分段Segi被判断为倍点或倍减操作之后，则可以联合分段Segi的前后的PLow特性进一步判断.倍减运算操作数-P=(x1,-y1)，而倍加运算操作为P，倍减运算的操作数前后需要重新读取操作数，因此Segi前后的PLow的耗时存在一定差异（即宽窄不同），若Segi的前后PLow宽，则可以判断次分段为倍减运算；Segi的前后PLow窄，则为倍加，如图5所示.

图5 倍点、倍加、倍减功耗特性Figure 5 Power consumption characteristics of point doubling,addition and subduction operations

2.3 椭圆曲线标量乘SPA攻击

根据1.2节中的算法2可知，NAF标量乘算法输入的正整数k值相关的运算在算法2的第1步进行，而倍点、倍加和倍点运算在算法的第3歩实现.其中若指数ki=0，则只进行倍点一种操作；若ki=1，则需倍点-倍加两种操作；若ki=-1，则需倍点-倍减两种操作.因此根据2.1节的功耗特性，通过分析标量乘功耗曲线映射的倍点、倍加、倍减操作可以估计出密钥NAF(k)值.如图6所示，ki的估计值依次为-1,0,0,1,0,-1,0,………………

因此根据2.1节功耗特征模型，标量乘SPA攻击步骤具体如下：

步骤1 首先根据功耗曲线PLow进行分段，得到分段集合Seg={Seg0,Seg1,………………,Segn}；

步骤2 分段集合Seg中每分段进行分类，得到分类簇集C={c0,c1,………………,cn}，分类原则：计算每段Segi的PHigh的功耗特性，若具有8个PHigh.则此段Segi为倍点，则ci=1；若具有13个PHigh，则再根据Segi的前后PLow的功耗特性；若Segi的前后PLow宽，则可以判断次分段为倍减运算，ci=2，Segi的前后PLow窄，则为倍加ci=3；

步骤3 根据分类簇集C，初值i=0，j=0；若ci=1，则判断ci+1=1，则kj=0，i=i+1，j=j+1；若ci+1=2，则kj=1，i=i+2，j=j+1；若ci+1=3，则kj=-1，i=i+2，j=j+1；循环直至i＞n结束；

步骤4 根据NAF(k)的值，最终求解出正整数k值.

图6 密钥k值的SPA攻击Figure 6 Simple power attack of the private key k

2.4 椭圆曲线标量乘SPA攻击防御

针对标量乘原子级的SPA攻击算法，可知攻击的前提倍点、倍加、倍减运算原子级的模乘操作、读取数据操作的功耗特征差异，以及两种运算的原子操作的数量差异，两种差异相结合可以明显区分倍点和倍加功耗.而根据算法2可知，倍点、倍加、倍减运算与k值存在依赖关系，从而推导出k值.因此防御方法可以从倍加、倍减、倍点原子级操作数量差异角度采用等功耗防御，即在标量乘实现过程中，可以在倍点运算中适时增加空模乘操作和相应的空模加等操作，如式(6)和(7)所示，在模加Pop_mod_add、模减Pop_mod_sub、移位Pop_shift、数据读取Pop_rw实现等功耗，避免不同操作的功耗特性出现时间差异.

式中，Rand为随机数函数.具体防御措施如表2所示.

在表2中，▲表示模乘空操作，★表示模加空操作.从表2的攻击防御可以看出，为了达到等功效，倍点和倍加分别相应增加了模乘和模加空操作，使倍点和倍加实现操作等功耗由式(6)和(7)变为式(8)和(9)所示：

模乘和模加空操作的加入，使倍点和倍加原子操作的数目一样，并且3类功耗特性的原子操作的功耗数目也一样，实现了原子级操作的等功耗，无法区分倍点和倍加运算而分析密钥值.另外空操作的加入也可以起到随机延迟的作用，使基于选择明文的侧信道攻击同样无效.

3 结语

区块链作为一种新兴的分布式框架协议，具有去中心化、去信任、匿名性、可追溯、不可篡改等独特的特性，已应用于许多领域.而密码技术是保证其安全特征最关键的计算，并且随着区块链实现技术的硬件化，侧信道攻击是对密码硬件行之有效的攻击手段.本文分析了区块连中的ECC算法的标量乘原子操作运算的功耗特征模型，提出了一种实用的SPA攻击方法，采集一条标量乘功耗曲线，可破解密钥.详细给出了原子操作级的等功耗防御方案，为区块链硬件设备提供的安全密码技术.

表2 原子级等功耗防御Table 2 Countermeasure of equivalent power consumption at atomic level