基于QPCA的彩色图像复制粘贴检测

王金伟，徐春晖

南京信息工程大学计算机与软件学院，南京210044

随着信息技术的发展，人们传递信息的媒介越来越多样化.图像是交流媒介中非常重要的组成部分.通过图像处理软件可以实现图像的修改，人们根据自己的意愿修改图像以便于使用，但有人会用修改过的图片来混淆视听或谋取利益.被篡改过的图片如果进入媒体、法庭等，会颠倒黑白，造成较差的社会影响.为了防止这种情况的发生，图像取证技术应运而生.该技术的目的是验证一幅图片是否经过伪造或篡改，其中图像盲取证是对未嵌入水印的待检测图片进行检测的技术.伪造图片的方法有很多种，复制粘贴伪造是使用最普遍的方法之一.复制粘贴伪造通过复制图片中的一部分粘贴到图片的另一部分中以达到修改图片内容的目的.伪造者经常使用这种手段隐藏图片中的某些内容，或强调图片中特定部分.由于复制粘贴操作的复制区域和粘贴区域均来自于同一幅图片，因此两者的特征基本类似，如说色温、噪声分布、光照条件等，这就加大了取证的难度.

目前，研究人员针对复制粘贴篡改提出了很多盲取证策略，主要可以分为基于块的[1-11]和基于点的[12-18]两大类.基于块的取证方法是将图像分成重叠的小块，提取每块的特征并进行比对，然后找出类似块的移位向量，当相同移位向量的数目大于某个阈值时，就认为该移位向量为可疑向量，两块间移位向量为可疑向量的块为篡改区和粘贴区；基于点的取证方法是在图像中找到类似的特征点，类似的一对特征点同样可以得到一个移位向量，当相同移位向量的特征点聚集在一起，则认为这些区域为可疑区域.在基于块的取证算法中，文献[1]总结了基于块的复制粘贴取证方法，并提出了基于块DCT特征的鲁棒匹配算法，相较于精确匹配，鲁棒匹配可以减少由于JPEG压缩而产生的漏检部分；文献[2]将每块转化为一个行向量，对所有行进行PCA变换，得到每行的PCA特征，这种算法提取了每块的主成分，提高了对有损压缩和加性噪声的鲁棒性；文献[3]首先运用颜色矩将相似块分类，再运用颜色布局描述算子提取特征找出篡改区域；文献[4]将图像划分为圆形的小块，计算每块的离散径向傅里叶矩作为特征，增强了算法对旋转操作的鲁棒性；文献[5]运用基于三角不等式的Kmeans算法，加快了DCT特征聚类的速度；文献[6]运用模糊不变矩作为特征；文献[7]运用Hu矩作为块特征；文献[8]运用Zernike矩作为特征；文献[9]对块进行奇异值分解，得到几何不变量作为特征；文献[10]将离散小波变换与奇异分解结合；文献[11]运用傅里叶梅林变换生成特征向量.基于点的取证算法中，文献[12-13]运用SURF特征点，文献[14-17]运用SIFT特征点.基于点的取证方法的差异主要在后续处理上，如误判点的排除.文献[17]还增加了一步预处理操作：先将图像分成互不重叠的部分，以提高计算速度.文献[18]将目前各种主流算法进行了详细的比较.

虽然目前有很多取证方法，但这些方法大多是针对灰度图像的.即便图像是彩色的，也会将彩色图像转换成灰度图像来处理，这样就忽略了各个通道之间的相关性，损失了大量信息.为了解决这一问题，研究人员将四元数运用于彩色图像处理.文献[19]将四元数小波变换运用于CG/PR图像的鉴别，充分利用了彩色图像的颜色信息，有效降低了特征信息的损耗，提高了检测准确率.文献[20]将四元数离散余弦变换运用于拼接图像的检测，对彩色图像进行四元数离散余弦变换得到变换系数，然后使用四元数马尔科夫方法提取特征，最后用支持向量机检测拼接图像，实验表明该方法优于大部分现有方法.文献[21]将四元数Zernike矩运用于彩色人脸识别.

本文针对上述彩色图像信息不能被有效且充分利用的问题，提出了一种基于QPCA的彩色图像取证算法.首先将彩色图像分成重叠的小块，将每一块用四元数表示，并用QPCA提取每块的特征.然后将所有特征进行字典排序，获取相似块的移位向量.最后依据移位向量出现的次数是否高于阈值来确定篡改区域，如果高于阈值，则判定该移位向量为可疑向量，对应区域为篡改区域.

1 四元数

四元数的概念是最简单的超复数.四元数由1个实部和3个虚部组成，即

式中，a、b、c、d为实数，i、j、k为虚数，且i、j、k满足

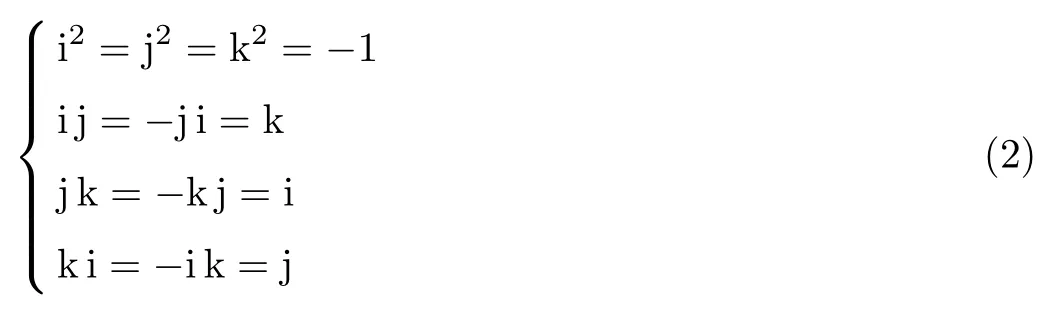
式中，四元数乘法不满足交换律.当a=0时，也就是四元数实部为0时，称四元数q为纯四元数.四元数的共轭和四元数的模分别为

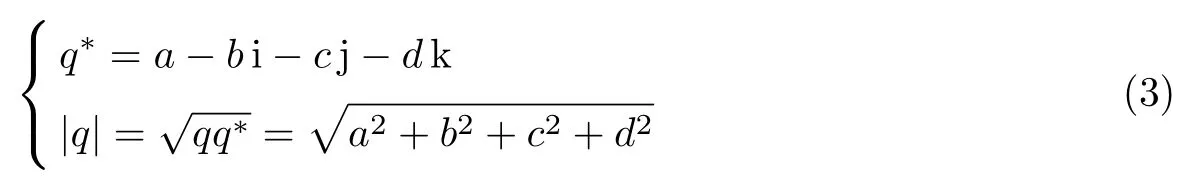
2 QPCA特征提取

2.1 QPCA变换

PCA（主成分分析）广泛用于减少数据集的维数，且能保持对方差贡献最大的特征.同时通过保留图像低阶主成分，忽略高阶成分，进而实现图像的主要特征提取.QPCA是PCA在四元数域的拓展.文献[22]简述了QPCA的定义如下：

假设对s个t维四元数数据进行PCA

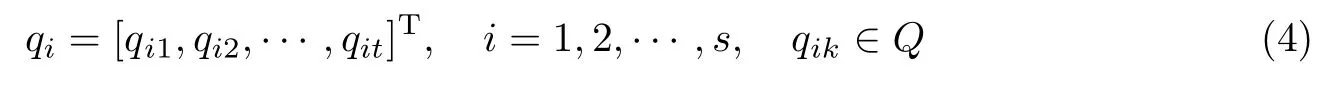
协方差矩阵定义为

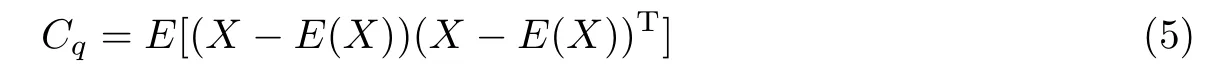
式中，X为样本，E(X)为平均值，代入数据得

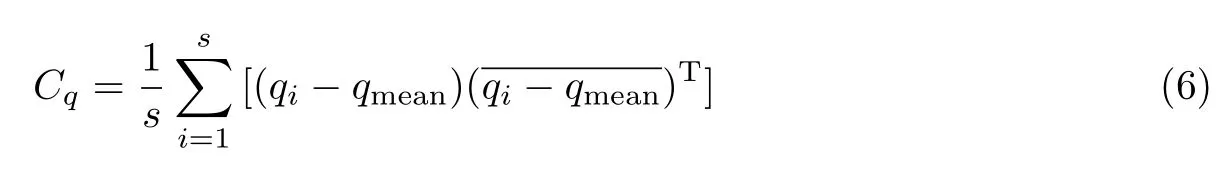
其中qmean表示样本均值

对协方差矩阵进行奇异值分解，分解后得到特征值及其对应的特征向量组成的矩阵Mq，设Nq=，那么qi的QPCA变换为

2.2 QPCA特征提取

一幅彩色图像可以用一个纯四元数矩阵Q∈Qmn表示为

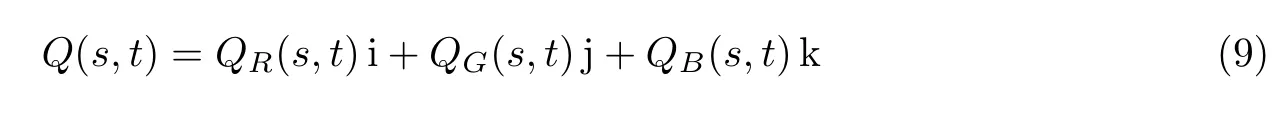
式中，QR(s,t)、QG(s,t)、QB(s,t)分别表示在彩色图像中坐标为（s,t）处R、G、B 3个分量的像素值，1≤s≤m,1≤t≤n.

文献[23]详细阐释了QPCA的定义：如果有N幅彩色图像{Qi∈Qmn,i=1,………………,N}，首先将所有彩色图像由矩阵拉伸为向量得到最终得到

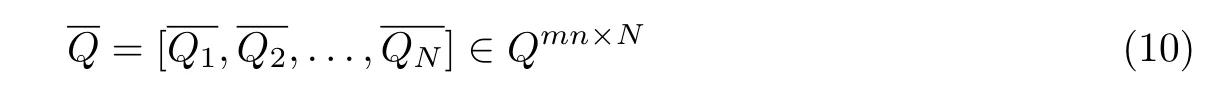
四元数协方差矩阵为

因为CX是四元数Hermitian矩阵，所以Ω是实对角矩阵.根据四元数特征值分解定理，WH的每一列是协方差矩阵CX的特征向量.每一幅彩色图像的特征向量可以表示为

将Ω的值按递减次序排列，选出占特征值总和一定比例的特征值.筛选出式(13)中WH中特征值对应的列，就得到了彩色图像的主要特征.

3 本文方案

经过QPCA变换的图像块，在保留颜色的同时降低了每个图像块的维度，获取了彩色图像特征，从而减少了后续的运算量，也增强了检测对噪声、有损压缩的鲁棒性.本文所提方法主要过程如图2所示，具体步骤如下：

步骤1 以四元数的方式读取一幅图像并将图像分为重叠的小块.

步骤2 对这些小块组成的矩阵进行QPCA变换得到每块的幅值特征

步骤3 将幅值特征量化后进行字典排序，得到相邻块的坐标和移位向量.找到满足条件的移位向量并根据坐标标定复制粘贴区域.

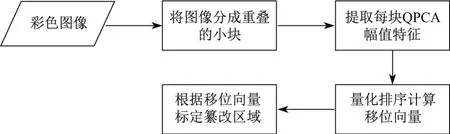
图1 本文方案的框架Figure 1 Framework of the proposed scheme

3.1 图像分块

以四元数的方式读取一幅图像，以1个像素为步长，将图像分为大小为k×k重叠的小块，一幅m×n的彩色图像可以分为(m-k+1)×(n-k+1)个彩色图像块.将每个彩色图像小块中的像素放到1个行向量中（这个行向量中每个元素都是四元数），这样就形成了1个(m-k+1)×(n-k+1)行，k×k列的四元数矩阵A.

3.2 提取QPCA幅值特征

对矩阵A进行四元数特征值分解，得到特征值和特征向量组成的四元数矩阵B.取前j个特征值，使这j个特征值之和占总特征值之和的比例为l%.则B的前j维组成的矩阵C为A经过QPCA变换后的矩阵.将四元数矩阵C的每个元素用其幅值表示，得到实数矩阵D.

3.3 量化排序计算移位向量

将矩阵D除以量化因子Qz，得到量化后的矩阵Eq.量化因子的选择非常重要，如果量化因子取值太小，会出现很多误检区；如果太大，会出现很多漏检区.量化后对E进行字典排序，得到排序后的矩阵F和索引I，这样相似图像块就会在矩阵F相邻行中.索引代表排序后的每一行在原矩阵中的行号.在将图像分块时，由于从图像左上角自上而下自左而右取图像块，因此每个图像块左上角的横坐标x为(I-1)mod(m-k+1)+1，纵坐标y为「I/(m-k+1).假设x、y组成的坐标矩阵为G，计算矩阵G两行之间的差得到移位向量矩阵H，H每行有两个元素，分别为Δx和Δy.为了排除距离相近的块的影响，设置移位向量长度距离阈值r，值为移位向量长度.如果矩阵H中第1列等于Δx并且第2列等于Δy的行数大于频率阈值f，且Δx和Δy满足则认为该移位向量是符合条件的移位向量.再在矩阵G中找出差值为该移位向量的坐标并标定即可.具体算法如下：

输入 待测彩色图像image（大小为m×n），块大小k，能量比阈值l，量化因子Qz，距离阈值r，频率阈值f

输出 篡改区域forgedregion

在H中找到符合条件的移位向量，并在G中找到其在图像中的坐标，在image中标定出坐标得到篡改区region.

4 实验

实验从选取的图像库、评价标准、阈值选择、对比实验4个方面来说明本文所提方法相较于传统方法的优越性.

4.1 选取的图像库

实验采用文献[16]所用的图像库，包含Dataset0、Dataset1、Dataset2、Dataset3 4个部分.其中，Dataset0为未经过其他操作的50幅彩色篡改图像以及每幅图像对应的真实篡改区域的二值图像.Dataset1和Dataset2分别为篡改区域经过旋转和缩放操作的篡改图像.Dataset3为Dataset0中每幅篡改图像对应的原始图像.图像格式为BMP，图像大小为1 024×768.本文算法不涉及旋转和缩放操作，因此选用图像库中的Dataset0和Dataset3.图像库中的一些样本如图3所示.

图2 图像库中的样本Figure 2 Samples in the dataset

4.2 评价标准

本文认为一幅图像在检测后被标定的篡改区与实际篡改区相同的面积越大，检测效果越好.也就是说，漏检区域与误检区域的和的面积占图像总面积的比率越小，算法对篡改区域的标定就越准确，检测正确率就越高.因此，本文将标定篡改区与实际篡改区进行异或操作，操作完成后值为1的部分即为误检或漏检区域，如图4所示.这些非0数值的和即为漏检区域和误检区域的像素和.最后计算所有图像的平均误检漏检率V为

式中，M为漏检区域的像素数；F为误检区域的像素数；P为图像的总像素数.

图3 评价标准Figure 3 Evaluation standard

4.3 阈值选择

实验阈值方面，块大小k取16，QPCA降维后能量占总能量的比例l=0.99，移位向量最小长度r=16，移位向量频率阈值f=20，量化因子Q=256.在其他变量不变的情况下，表1为移位向量频率阈值f在15～25时平均误检漏检率V的变化；表2为量化因子Q在192～320时平均误检漏检率V的变化；表3为能量比l在0.97～0.99时平均误检漏检率V的变化；实验表明当f=20，Q=256，l=0.99时，V最小，实验结果最好.

表1 不同移位向量频数的平均误检漏检率的比较Table 1 Average errors of different shift vector frequency

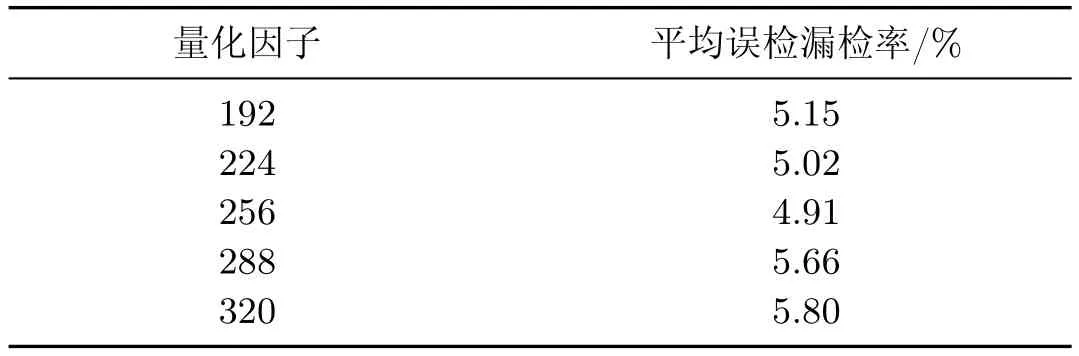
表2 不同量化因子下的平均误检漏检率的比较Table 2 Average errors of different quantitative factor

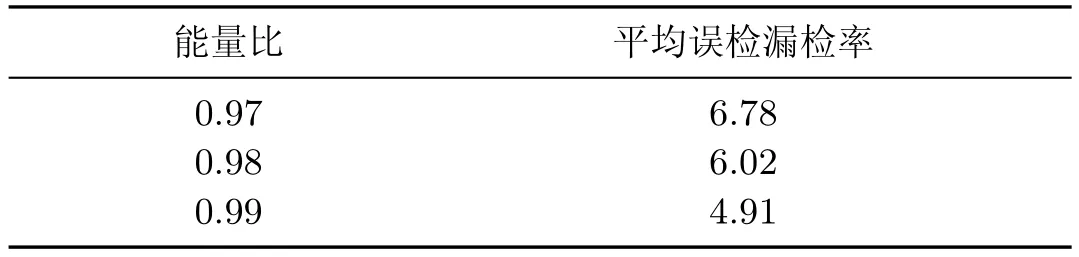
表3 不同能量比的情况下平均误检漏检率的比较Table 3 Average errors of different energy ratio%

4.4 对比实验

表4将本文方法与其他取证方法及传统PCA取证方法进行比较.其中文献[2]的方法是基于传统PCA特征的，文献[5]所用方法是基于快速DCT特征的.但文献[2]与文献[5]在预处理时均将彩色图像转化为灰度图像，滤除了图像的颜色信息.实验结果表明，本文方法的平均误检漏检率低于其他两种算法.图5展现了在相同量化因子、分块大小、距离、能量比例、移位向量频数的情况下基于PCA特征的算法和本文方法检测结果的对比.结果表明，将彩色图像转化为灰度图像之后，非篡改区域具有相似主成分和相同移位向量的块会被误判为篡改区域.运用本文所提的QPCA方法后，由于充分利用了色彩信息及RGB通道之间的相关性，进一步扩大了非篡改区域与篡改区域之间的区分度，因此有效降低了误检漏检率.

表4 不同算法的平均误检漏检率的比较Table 4 Comparison in average errors of different methods

图4 实验结果对比Figure 4 Comparison of experiment results

5 结语

本文将四元数引入彩色图像复制粘贴检测中，与传统将彩色图像转化为灰度图像再进行检测相比，用四元数表示彩色图像后提取四元数主成分特征，在保留了图像原始颜色信息的情况下实现了图像特征的提取，降低了篡改检测的误检漏检率.然而，由于复制粘贴取证中有些变量需要通过反复实验和人为决定，如最佳分块大小、量化因子、移位向量频数等.这些变量会根据图像大小而变化，因此下一步工作将针对这些因素继续深入研究，以求把人为干预降到最低，同时也将围绕针对缩放与旋转操作的彩色图像取证问题展开研究.