基于粒子群优化的DGM(1,1)模型在基坑变形安全预测中的研究*

陈家骐，华建兵，段园煜，司大雄，丁 蕾，丁碧莹

(合肥学院 建筑工程系，安徽 合肥 230601)

0 引言

基坑变形预测是工程监测中非常重要的内容之一。变形预测可以让施工人员根据现有监测数据，预测到未来可能发生的问题，及时制定措施保证工程安全进行。因此，进行基坑变形预测尤为重要。比较常见的预测方法如遗传算法、BP神经网络和支持向量机等[1-6]，但所需样本较多，而离散灰色预测模型DGM(1,1)具有所需样本总量少、模型简单易于计算等特征，已经被广泛用于基坑变形预测中。实际工程应用中，由于模型本身一些缺陷，如背景值和初始值确定方法等，经常会出现预测精度不足的情况。许多研究人员从构造模型本身参数出发，利用粒子群算法对模型进行优化[7-8]。然而，将原始数据利用变权缓冲算子结合粒子群算法进行降噪处理的优化方法却少有研究。除此之外，许多利用粒子群算法优化灰色模型的研究中，只用平均相对误差和均方差等单一函数作为适应度函数对模型参数进行优化[9-10]，不同目标适应度函数对模型参数优化影响的研究也比较少见。

对此，本文提出1种基于粒子群算法优化的变权离散灰色预测模型，称为PSO-VWDGM(1,1)模型。利用变权缓冲算子和粒子群算法对原始序列进行降噪处理，提高原始序列的光滑度，从而提高预测精度。利用相对误差检验、后验差比检验、灰色绝对关联度检验3种精度检验方法作为粒子群算法目标适应度函数建立模型，研究不同目标适应度函数对模型参数优化的影响。研究成果在基坑变形安全评估、预警方面具有应用价值。

1 灰色预测模型

1.1 离散灰色预测模型

定义1[11]：设序列X(0)={x(0)(1),x(0)(2)，…,x(0)(n)},其中x(0)(k)≥0,k=1,2,…,n，则称X(1)={x(1)(1),x(1)(2),…,x(1)(n)}为序列X(0)的一次累加生成序列，其中：

(1)

定义2[12]：设序列X(0),X(1)如定义1所述，则称：

x(1)(k+1)=β1x(1)(k)+β2

(2)

为离散灰色预测模型DGM(1,1)，其中β1，β2为估计参数。

对式(2)使用最小二乘法，则离散灰色预测模型的估计参数β1，β2满足：

(3)

其中：

(4)

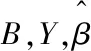
k=1,2,…,n-1

(5)

1.2 变权弱化缓冲算子

定理3[13]：设X=(x(1),x(2),…,x(n))为非负的系统行为数据序列，令：

XD1=(x(1)d1,x(2)d1,…,x(n)d1)

(6)

其中：

x(k)d1=λx(n)+(1-λ)x(k)

(7)

式中：λ为可变权重，0<λ<1；k=1,2,…，n。当X为单调增长序列、单调递减序列或震荡序列时，称D1为变权弱化缓冲算子。

1.3 精度检验[14]

1)平均相对误差a

(8)

2)后验差比C

C=S2/S1

(9)

式中：εs(u)为预测值和拟合值的残差；S1为原始序列的标准差；S2为拟合序列与原始序列残差序列的标准差。

3)灰色绝对关联度

(10)

(11)

(12)

式中：s0和s1分别为原始数据和拟合数据的灰色绝对关联度计算参数。灰色模型精度等级如表1所示。

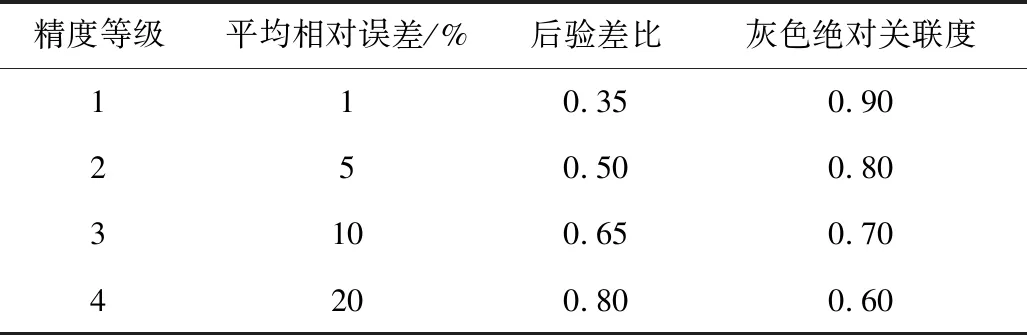
表1 灰色模型精度等级Table 1 Gray model precision grade

1.4 多种缓冲算子的优化模型

为了解决系统由于外界冲击扰动而导致数据离乱的问题，刘思峰等[13]提出冲击扰动系统和缓冲算子的概念, 并构造出平均弱化缓冲算子；党耀国[13]构造了几何平均弱化缓冲算子、加权平均弱化缓冲算子、加权几何平均弱化缓冲算子等具有普遍意义的实用算子。上述几种缓冲算子均能有效改进优化灰色模型，有效解决定量研究结果与定性分析结论不符的问题。但是上述缓冲算子在实际运用时, 往往难以得到令人满意的效果。因为传统缓冲算子不能实现作用强度微调, 导致缓冲作用效果过强或过弱，难以还原数据本来面目。王正新等[14]提出的变权缓冲算子通过多种数学算法测算并调整可变权重的大小来控制缓冲算子作用强度，可以更精准地还原数据本来面目。智能数学算法中的粒子群算法同遗传算法相比，更加容易实现，且没有许多需要调整的参数，具有计算速度快、收敛速度快的特点。运用粒子群算法定量测算变权缓冲算子可变权重可以快速准确得到最优权重，并运用多种精度检验函数作为粒子群算法的适应度参数函数，研究测算可变权重时的最优函数问题。

2 粒子群算法优化的灰色模型

2.1 粒子群算法原理

假设在D维空间中有m个粒子，粒子i在D维空间的位置向量为xi=(xi1,xi2,…，xiD),粒子i在D维空间的速度向量为vi=(vi1,vi2,…，viD)。将粒子的空间位置向量带入目标函数f(x)求得适应度值，根据适应度最大或最小准则判断该位置是否为最优位置。个体粒子i飞过历史最好位置为pi=(pi1,pi2,…，piD)，群体中所有粒子飞过的最好位置为pg=(pg1,pg2,…，pgD)[15]。粒子群算法中的粒子速度和位置按如下公式进行更新。

速度更新公式：

(13)

位置更新公式：

xiD(t+1)=xiD(t)+viD(t+1)

(14)

式中：t为迭代次数；viD为第i(i=1,2,…,m)个粒子在第D维空间的速度，m/s；xiD为第i个粒子在第D维空间的位置，m；piD(t)代表第i个粒子在第D维中迭代t次时最好的位置，m；pgD(t)代表粒子种群在第D维空间中迭代t次时最好位置，m；ω为惯性权重；c1为自我学习因子；c2为群体学习因子；r1,r2为[0，1]区间内的随机数。

2.2 基于粒子群算法的建模过程及参数设置

建模过程如下：

1)初始化设置：惯性权重w一般取0.8；学习因子c1,c2在0～4之间，一般跟自变量的取值范围有关，取c1=c2=0.5；迭代次数t取值过大会导致计算变慢，过小导致计算精度不足，取t=30；PSO-VWDGM(1,1)模型中待优化参数λ作为一维空间种群中的个体粒子，初始种群的粒子个数取i=50；初始粒子的速度vi及位置xi采用随机数函数给出，由于待定参数λ的取值范围在0～1区间内，所以位置xi的取值范围限制在[0，1]；为防止粒子飞行速度过快而飞出限制范围，速度vi取[-1，1]。

2)适应度值计算：利用式(8)～(10)3种函数作为粒子群算法的目标适应度函数分别计算适应度值。

3)个体极值与全局最优解：将随机生成的初始种群粒子λ带入PSO-VWDGM(1,1)模型进行适应度值计算，并采用式(14)和(15)更新粒子的速度和位置。个体极值为每个粒子找到的历史上最优的位置信息pbest，并从这些个体历史最优解中找到1个全局最优解gbest，与历史最优解比较，选出最佳的粒子λ作为当前的历史最优解。

4)循环迭代计算：根据式(13)和(14)判断目标适应度函数值是否满足要求，如不满足要求则继续迭代计算至满足最优准则或最大迭代次数。

5)计算结束：计算结束后得到预测模型最优参数λ。

6)预测模型建立：使用求得的最优参数λ构造PSO-VWDGM(1,1)模型，并利用该模型进行预测。

3 应用实例

安徽省合肥市云谷路地铁车站位于云谷路和庐州大道的交叉口。基坑采用明挖顺筑法施工，该基坑共有4个立柱用于支撑混凝土，每个立柱顶部设立1个沉降观测点，点号为LZ1～LZ4。选取LZ4测点4月17日—26日的沉降数据，建立DGM(1,1)模型，用平均相对误差、后验差比和灰色绝对关联度为粒子群算法目标适应度函数建立3个PSO-VWDGM(1,1)模型。设上述4种模型分别为1号、2号、3号和4号模型。其中前6 d数据作为原始数据建立模型，后4 d数据用于预测值比对，检验预测模型的精度。表2为立柱沉降数据，选取前6个数据作为原始数据带入PSO-VWDGM(1,1)模型，用PSO算法优化模型并求得上述3种预测模型最优可变权重λ1，λ2和λ3，最优可变权重如表3所示。

表2 立柱沉降数据Table 2 Settlement data of columns

表3 最优可变权重λTable 3 Optimal variable weights λ

设粒子种群数量为50，迭代上限为30次。模型2的最优粒子搜索过程如图1所示，2号模型在迭代18次后，适应度趋于稳定，模型平均相对误差为定值，此时求得最优可变权重为0.026 21。模型3的最优粒子搜索过程如图2所示，3号模型在迭代21次后，适应度趋于稳定，模型后验差比为定值，此时求得最优可变权重为0.000 24。模型4的最优粒子搜索过程如图3所示，4号模型在迭代10次后，适应度趋于稳定，模型灰色绝对关联度为定值，求得最优可变权重0.051 78。

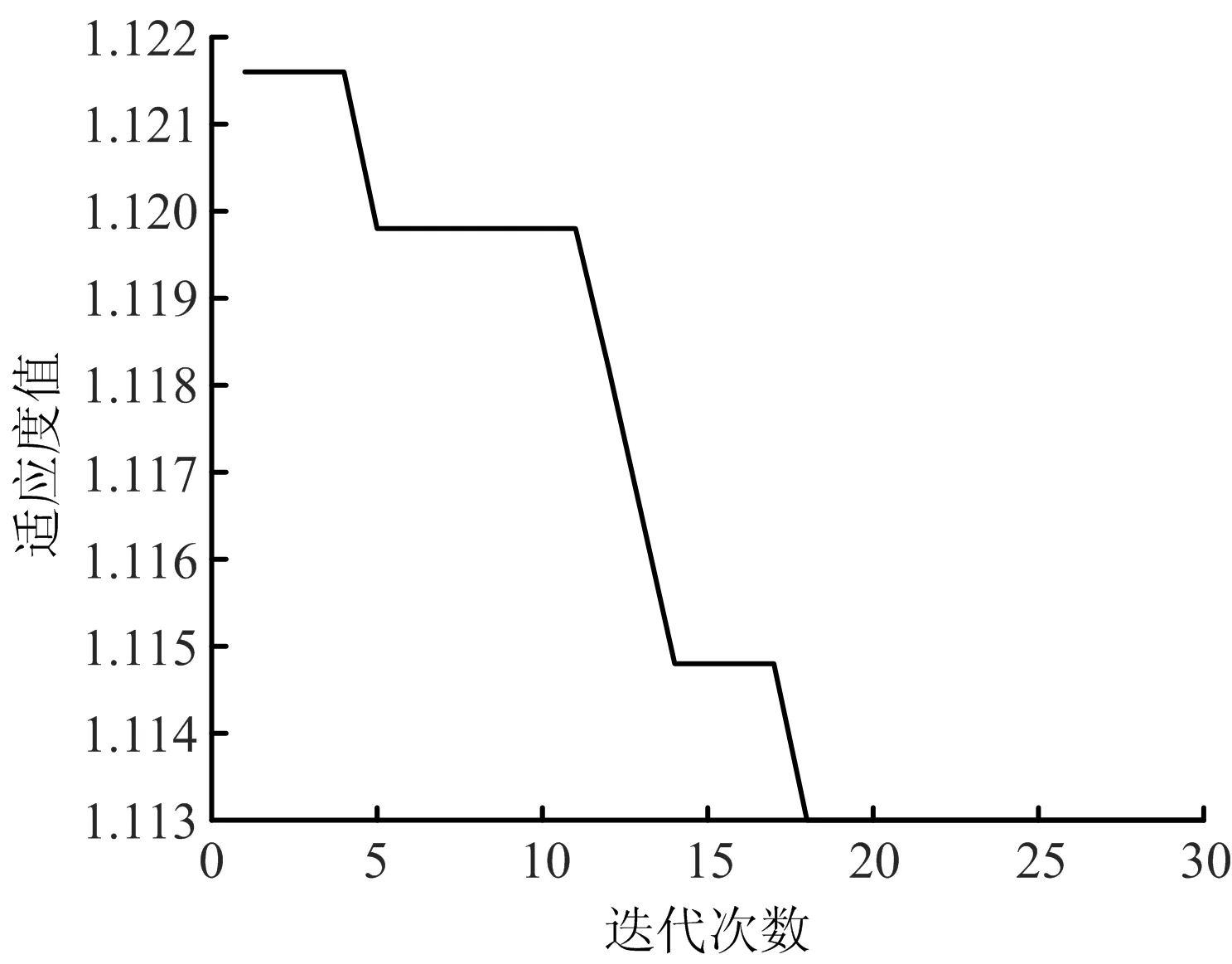
图1 模型2的最优粒子搜索过程Fig.1 The optimal particle search process for model 2

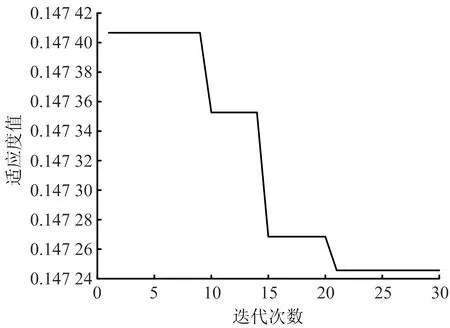
图2 模型3的最优粒子搜索过程Fig.2 The optimal particle search process for model 3

图3 模型4的最优粒子搜索过程Fig.3 The optimal particle search process for model 4

将表3中的可变权重λ代入式(6)和(7)中，对表2前6个原始数据进行降噪处理，构造PSO-VWDGM(1,1)模型。其中1～4号预测模型的方程分别为(k=1,2,…,n-1)：

(15)

(16)

(17)

(18)

利用上述4个方程求出的拟合值及预测值，见表4，用式(8)～(10)检验4种模型预测性能，检验结果见表5。

由表4可知，用变权缓冲算子和PSO算法构造的2～4号模型的拟合值及预测值相比传统1号DGM(1,1)模型更加接近真实值。由表1和表4可知，4种模型的预测精度均已经达到1级精度， 2～4号模型预测值的平均残差、平均相对误差、后验差比和灰色绝对关联度均优于1号模型。说明利用PSO算法和变权缓冲算子构造的PSO-VWDGM(1,1)模型的预测精度更高，优于传统DGM(1,1)模型。

根据表3、表5和图4对2～4号模型的比对可知，将不同的精度检验方法作为PSO算法的目标适应度函数得出的最终结果存在明显差异。3号模型(后验差比检验)作为PSO算法的目标适应度函数时，得到优化后的可变权重为0.000 24，利用该参数建立模型得到预测值的平均残差、平均相对误差、后验差比和灰色绝对关联度分别为0.414 7,2.533 3%,0.377 2和0.986 7，均略大于传统DGM(1,1)模型，是3种PSO-VWDGM(1,1) 模型中精度等级最低的模型。2号模型(平均相对误差检验)作为PSO算法的目标适应度函数时，得到优化后的可变权重为0.026 21，利用该参数建立模型得到预测值的平均残差、平均相对误差、后验差比和灰色绝对关联度分别为0.396 7,2.427 6%,0.371 1和0.987 7，均大于传统DGM(1,1)模型，是3种PSO-VWDGM(1,1)模型中精度等级位于中间的模型。4号模型(灰色绝对关联度检验)作为PSO算法的目标适应度函数时，到优化后的可变权重为0.051 78，利用该参数建立模型得到预测值的平均残差、平均相对误差、后验差比和灰色绝对关联度分别为0.336 2，2.068 2%，0.342 4和0.999 0，均大于传统DGM(1,1)模型，是3种PSO-VWDGM(1,1)模型中精度等级最高的模型。4号模型的预测值平均残差与2号和3号模型相比，精度分别提高了15.24%和18.93%；其预测值的平均相对误差与2号和3号模型相比，精度分别提高了14.8%和18.35%；预测值的后验差比与2号和3号模型相比，精度分别提高了7.71%和9.21%；预测值的灰色绝对关联度分别提高了0.23%与0.34%。

表4 不同模型拟合预测值及残差Table 4 Fitting predicted values and residuals of different models

表5 不同模型预测值的精度检验Table 5 The accuracy test of the predicted value of different models

为了更加直观的看出1至4号模型预测精度的大小关系，将这4中模型预测结果绘制如图4所示。由上述分析可知，在本工程实例的3个 PSO-VWDGM(1,1)模型中，4号模型具有最高的预测精度，2号模型次之，3号模型最差。但是3个模型的预测精度均为1级，均可适用于此工程。

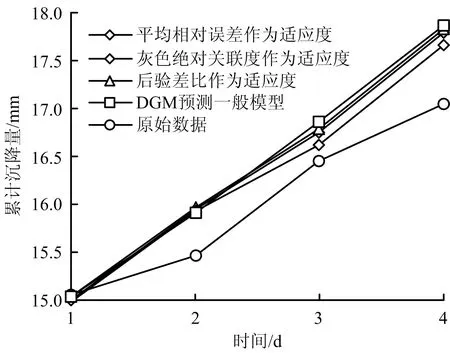
图4 预测结果对比 Fig.4 Comparison of prediction result

4 结论

1)利用变权缓冲算子对原始数据序列进行降噪处理，提高原始序列的光滑性，并通过PSO算法优化可变权重λ构造出PSO-VWDGM(1,1)模型，从而达到调节缓冲算子作用强度的目的，实现变权缓冲算子对原始数据序列作用强度的量化与控制。

2)相对误差检验、后验差比检验，灰色绝对关联度检验3种精度检验方法作为PSO算法目标适应度函数建立的模型相比传统DGM(1,1)模型，其预测精度高，预测性能更好。

3)比较3种PSO-VWDGM(1,1)模型可知，以灰色绝对关联度检验作为PSO算法的目标适应度函数的模型具有较好的预测精度。3种PSO-VWDGM(1,1)模型均具有1级精度，可以很好地应用在工程中。研究结果能为工程施工阶段的基坑变形预测、稳定性分析与灾害评估、预警提供指导。