用τ-p变换提取水中声源激发的海底Scholte波

王泽明，程广利，孟路稳，罗夏云



用-变换提取水中声源激发的海底Scholte波

王泽明，程广利，孟路稳，罗夏云

(海军工程大学电子工程学院，湖北武汉 430033)

水中声源激发的海底地震波场成分复杂，为了将Scholte波从地震波场中分离出来，基于-变换法，先将波场从-域变换至-域，利用Scholte波与其他波在该域中的特性差异，提取Scholte波，然后将其反变换回-域，从而获得Scholte波。针对-变换过程中固有的假频效应和端点效应，理论分析了各自的产生机理，分别采用限制波慢度和添加时间窗等方法抑制这两种效应。基于高阶交错网格有限差分法，给出了水中脉冲声源激发出的地震波场，并分析了其波动成分及特性，利用上述方法提取地震波场中的Scholte波，仿真结果证明了该方法的有效性。

舰船地震波场；Scholte波提取；-变换法；端点效应；假频效应

0 引言

随着减振降噪技术的发展，舰船中高频段的噪声得到了有效控制，但对于甚低频(如：50 Hz以下)噪声仍难以有效控制。舰船在海洋中航行时，这些波长的噪声经浅海海水传播至海底，从而在海底激发出甚低频舰船地震波场[1]。浅海舰船地震波成分主要包括Scholte波和简正波[2]，且Scholte波的能量在垂直方向上离开海底后迅速衰减，主要集中在一个波长深度内；在水平方向衰减慢，几乎不受海洋水文环境的影响，故可在海底远距离的传播，并可被对方侦测到。因此，从舰船地震波场中分离出Scholte波，具有潜在的军事应用前景。

有关从水中声源激发的海底地震波中分离出某一成分的方法，多集中于海底勘探信号处理中。而变换法常被用于分离易于激发和接收的纵波，以及能量大、分辨率高的横波[3-5]。在处理过程中，通常将包括Scholte波在内的其他波(除一次反射波外的直达波、透射波、滑行波、折射波和多次反射波)当成杂波滤除掉。

本文基于-变换法，通过选取合理的波慢度参数和添加时间窗的方法，克服变换过程中固有的端点效应和假频效应，提取了由脉冲声源激发的地震波场中的Scholte波，仿真数据验证了该方法的有效性。

1 τ-p变换理论

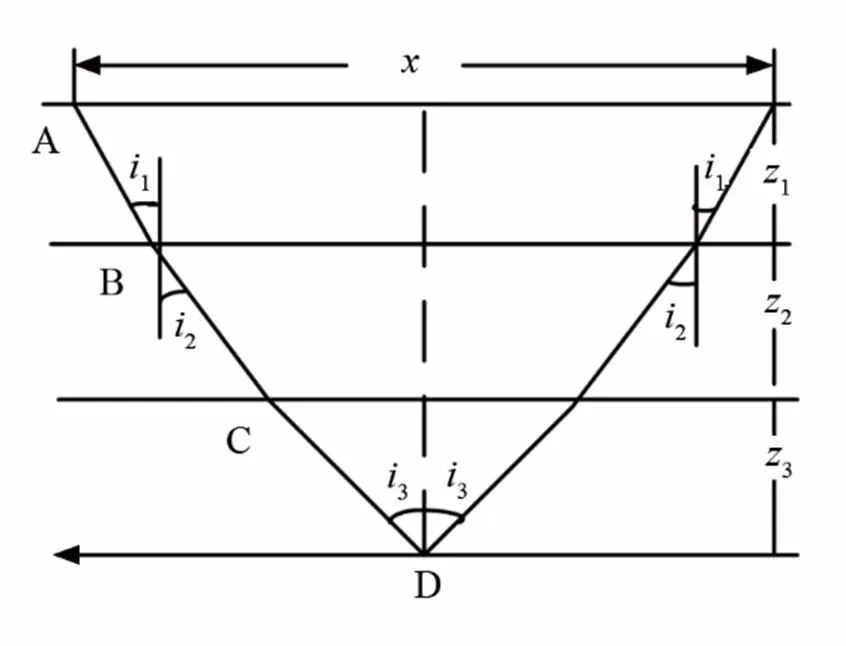
图1 声波在分层介质中的传播路径

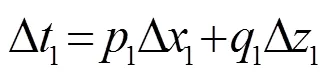
将图1中分层介质模型扩展到层分层介质模型，则有

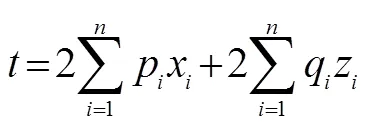
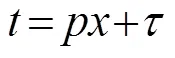
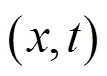
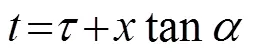
由于，得到的式(4)与式(3)相同。在τ-p变换的过程中，是切点斜率，是切线在时间轴上的截距。

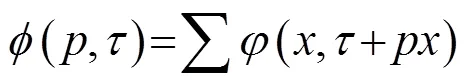
-反变换就是对-域中的曲线进行倾斜叠加，将信息反变换至-域中。那么截距点即为，于是-反变换的公式为

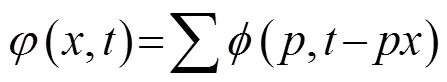
2 数值仿真及分析

基于高阶交错网格有限差分法[6]，仿真出水中脉冲声源激发的海底地震波场(为减少篇幅，文中从略)。仿真参数设置如下：硬海底条件，海水深度为200 m，海水密度和声速分别为1 000 kg.m-3、1 500 m.s-1，海底介质密度为2 300 kg.m-3，纵波速度为3 500 m.s-1，横波速度为1 800 m.s-1。声源采用雷克子波，深度为190 m，中心频率为20 Hz。

为减少仿真时的计算量，设置方向波场不变，将三维空间简化为二维，选定计算区域为520 m× 520 m，采用完全匹配层作为吸收边界[7]，声源所在的坐标为(260 m, 190 m)。在坐标范围为(260 m, 200 m)～(520 m, 200 m)的海底直线区域内，按1 m间隔仿真计算地震波场振幅。声源激发后0.1 s时刻的垂直正应力的波长快照如图3所示，1是直达声波，2是反射声波，3是Scholte波，4是透射横波，5是透射纵波，6是侧面波，7是泄漏瑞利波。

观察图3可知：在海水中传播的波场成分为1、2和6，其中1和2的波阵面按球面扩展，6的波阵面的上沿与2的波阵面相切，下沿在分界面处与4的波阵面相交；在海水与海底分界面附近产生表面波3，其波阵面沿分界面传播；在海底介质中传播的波场成分为4、5和7，其中4和5的波阵面按球面扩展，7的上沿与分界面相交，下沿与4相切。

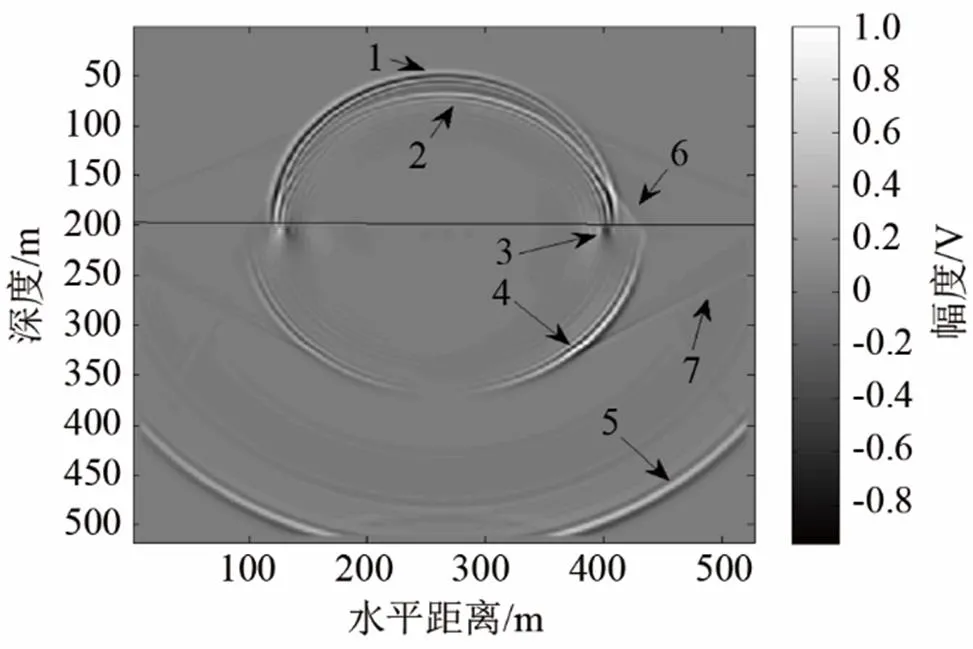
1-直达声波，2-反射声波，3-Scholte波， 4-透射横波，5-透射纵波，6-侧面波，7-泄漏瑞利波

本文中对所有伪彩图进行归一化处理，每幅图中的振幅最大值定为1。图4为-域中的原始波场，其中图4(a)是检波器接收到的舰船地震波场，可以观察到波场由多条斜率不相等的能量射线以及多条双曲线组成，前者由直达声波、Scholte波、透射横波、透射纵波、侧面波、泄露瑞利波等组成，后者由反射声波所致。

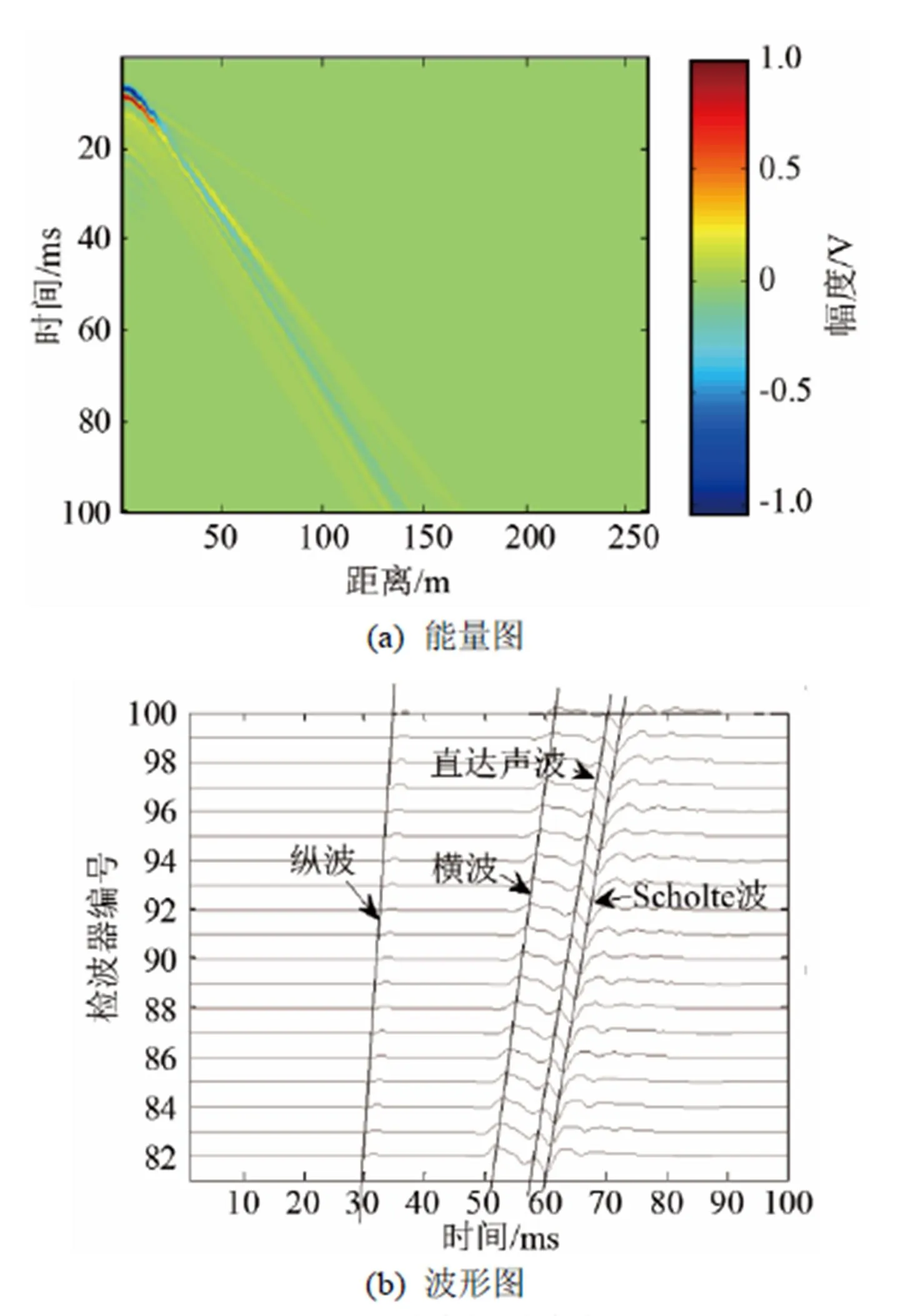
图4 t-x域中的原始波场

图4(b)为选取坐标(342 m, 200 m)～(360 m, 200 m)范围内的海底19个距离点处的波场振幅时域波形图，根据各直达波动成分的波速不同，在图中将它们标示出来。图5是经-变换后的波场。

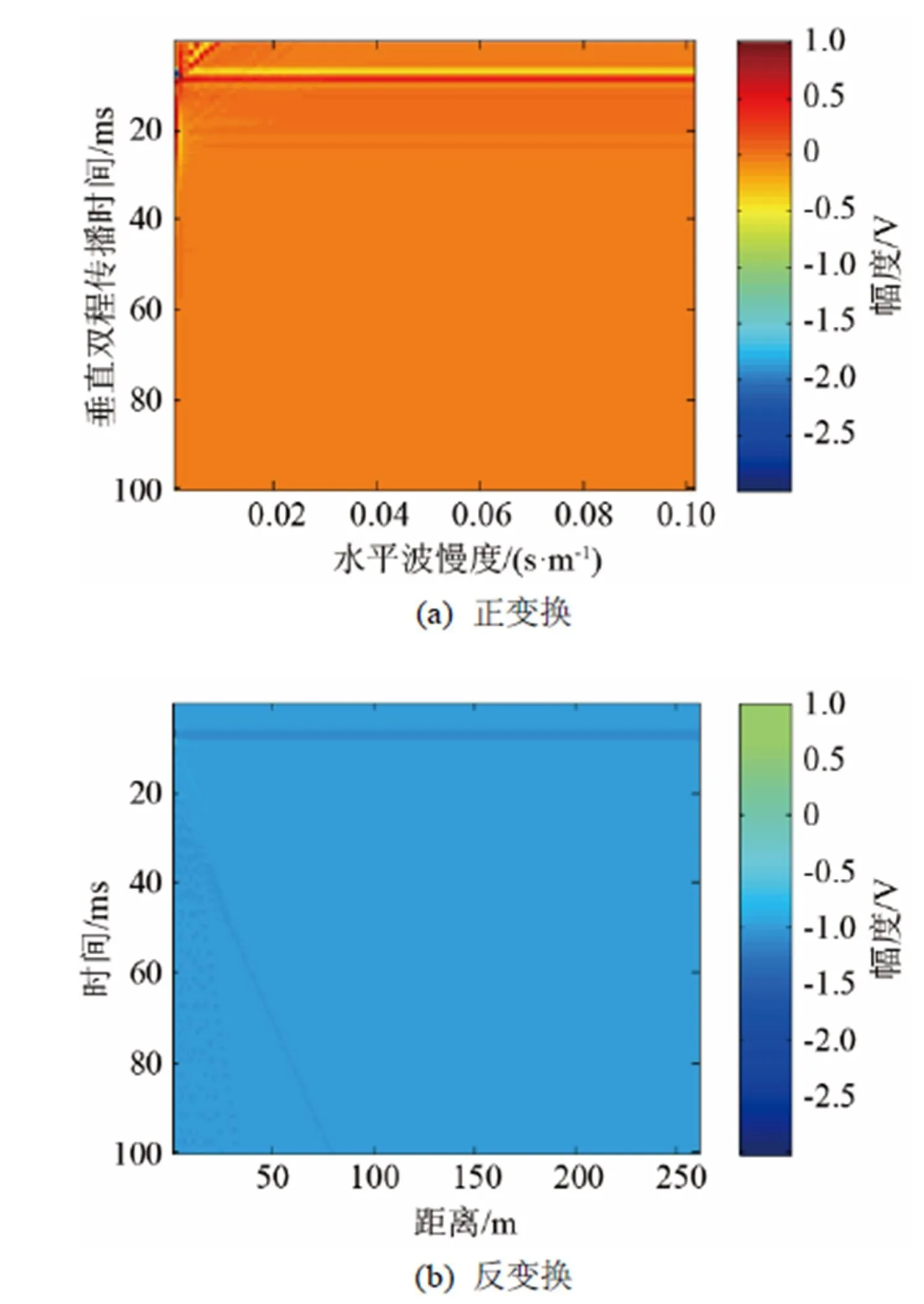
图5 τ-p变换后的波场

从理论上进行分析[4]，由式(2)可得

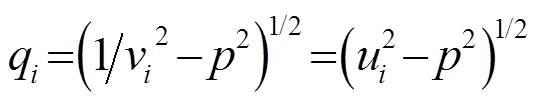
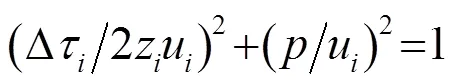
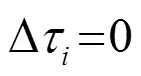
观察图5(b)可知，每条射线周围都有散射的能量薄层环绕，能量束之外的区域所占能量的比例增大，这就是所谓的端点效应。

这两种效应使得-域中的能量分散严重，势必导致无法通过反变换重建波场成分。

2.1 假频效应抑制

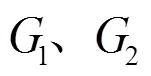
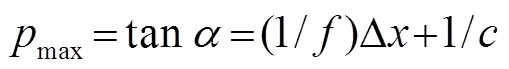
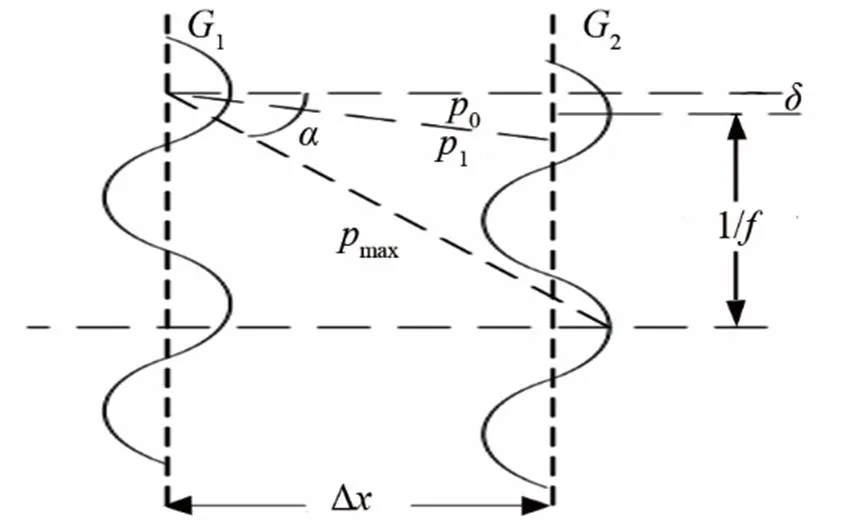
图6 假频效应示意图

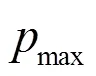
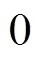
对比图7(b)、图5(b)以及图4，发现图5(b)中完全无法发现能量束，图7(b)中可以明显观察到图4(a)中的能量束，但是其宽度明显展宽，说明还要继续对端点效应进行抑制。

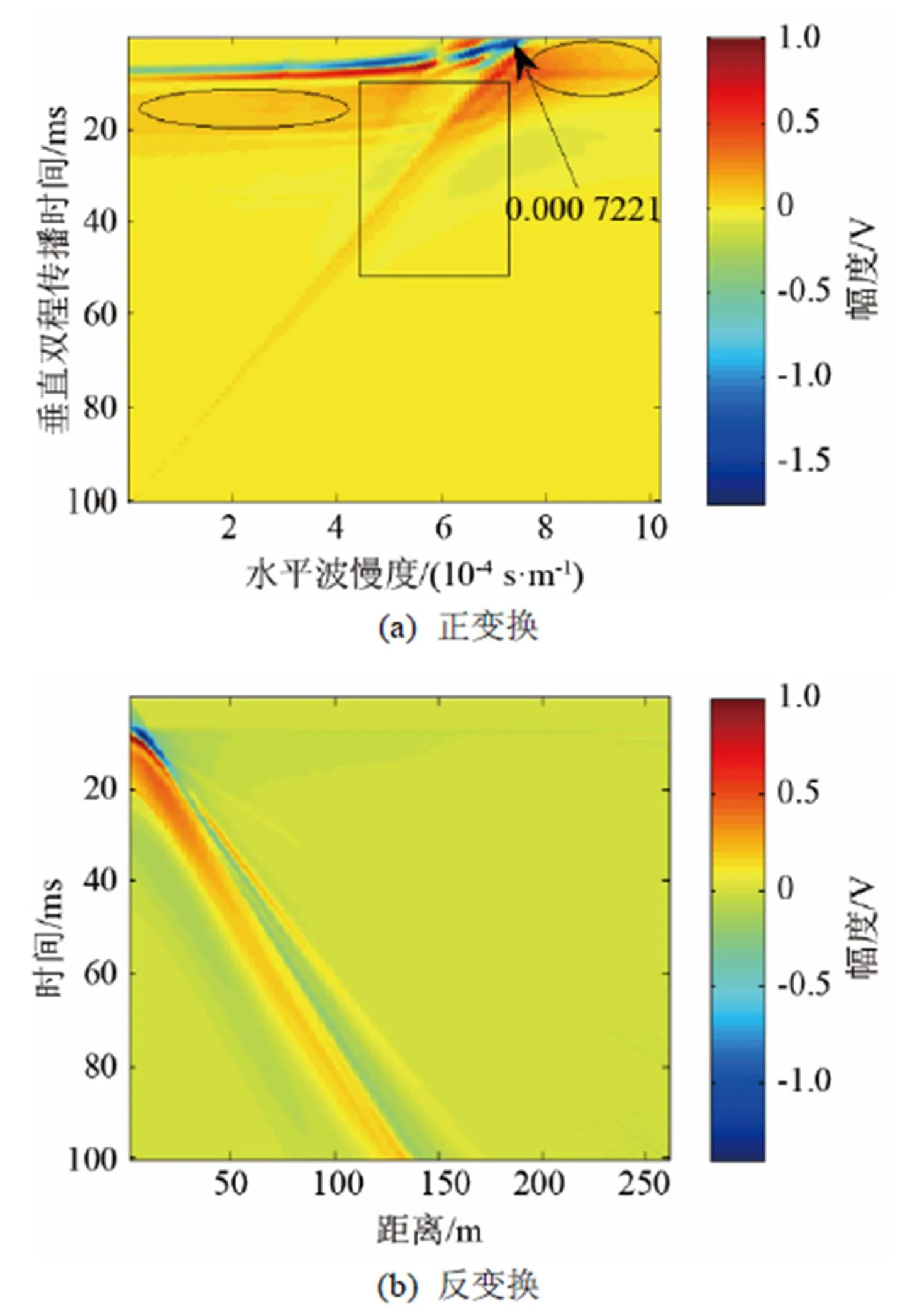
图7 假频效应抑制后的波场

2.2 端点效应抑制

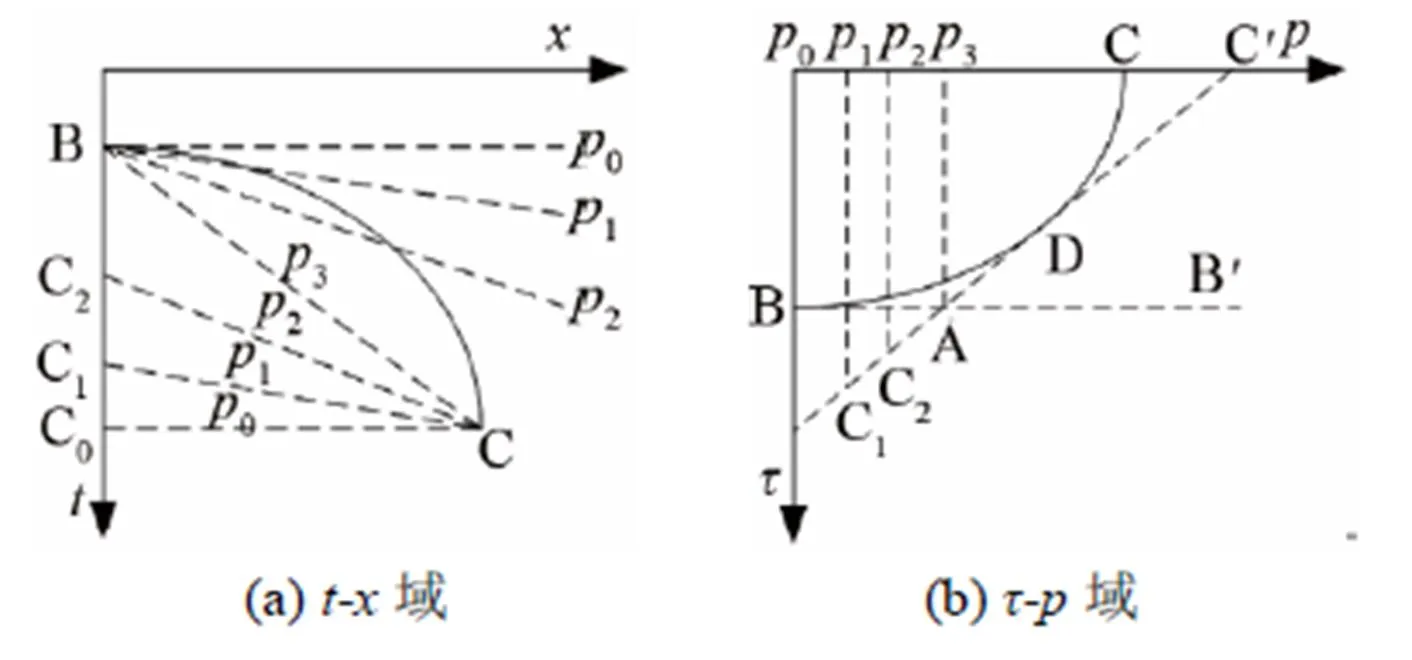
图8 端点效应示意图

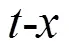
为了抑制端点效应，本文采取只让某点及其附近少量点参与倾斜叠加过程，因此采用添加时间窗的方法。时间窗选定的原则如下：

考虑到

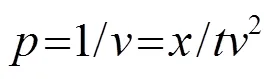
因此，在已知波速的情况下，对于一个固定的波慢度p，一定有若干个数据对满足式(11)。如图9所示，假设波慢度p与3条声线相切，取式(11)中的v为一个区间，那么只有两条射线、所夹区域的点才能参加倾斜叠加过程，从而可以有效避免端点的干扰，抑制端点效应。

处理后的波场如图10所示。对比图10(a)和图7(a)可知，两个圆圈区域因端点效应而产生的能量散射分别被有效抑制，但是方框区域内的能量散射只得到了一定程度上的抑制。因为方框区域同时受到近、远端点效应影响，干扰不易被完全消除。对比图10(b)、图7(b)以及图4，发现图10(b)相比于图7(b)，波场的能量束宽度被有效压缩，而且能量束之外的区域所占能量比例与原波场基本相同，证明了本文端点抑制方法的有效性。图10(b)相比于图4，能量束还是略有展宽，这是因为当端点附近的点进行倾斜叠加时，无论时间窗取值多小，总有端点可以满足时间窗条件，从而参与叠加。对比图10(c)和图4(b)，基本还原了时域的波形图，说明本方法基本将-域的波场重建出来。

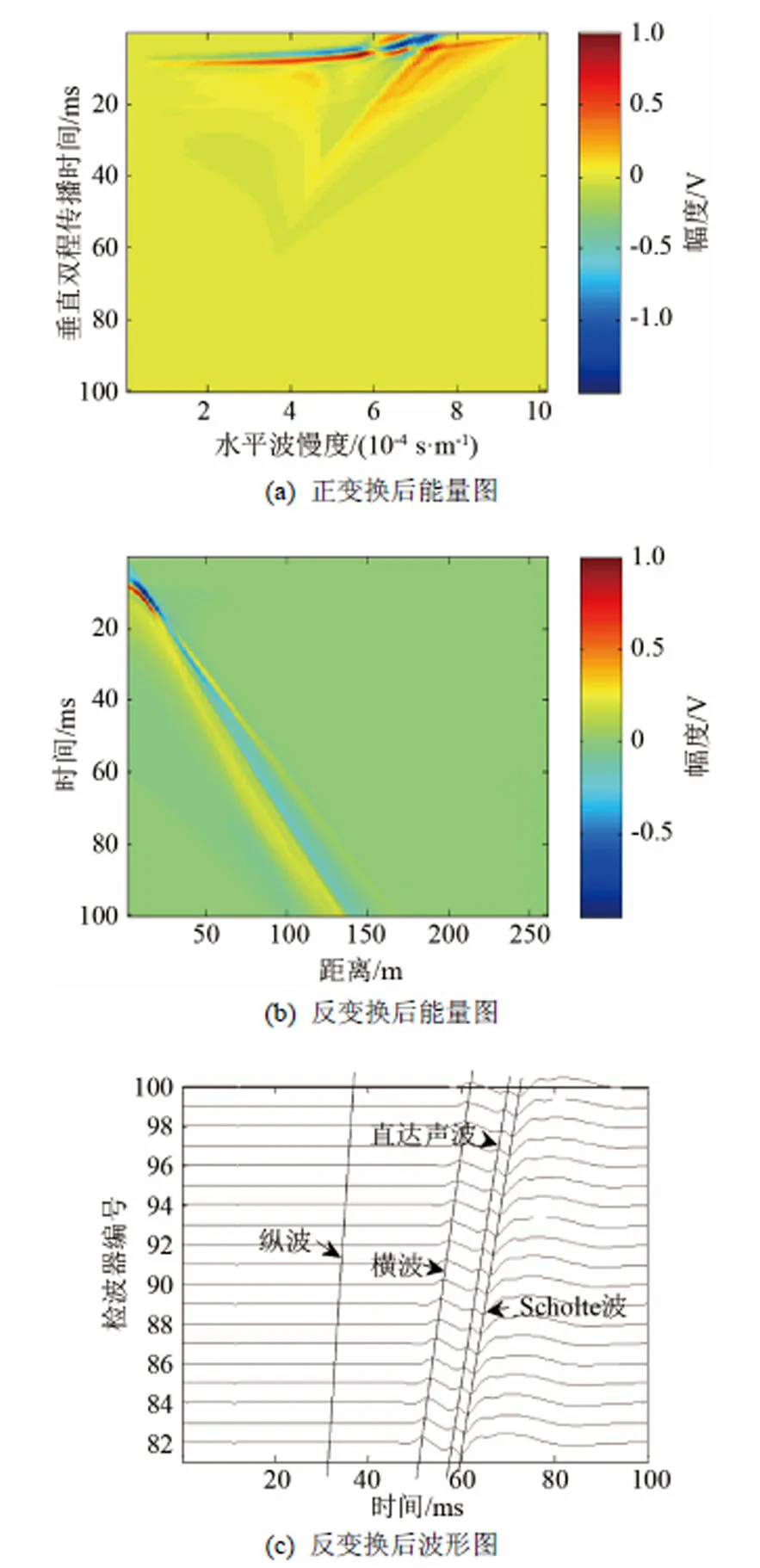
图10 假频和端点效应抑制后的波场

2.3 提取Scholte波

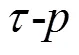
观察图11(a)可以发现，Scholte波在-域中是一条斜率不变的直线，幅值相对较大，再次验证了硬海底情况下Scholte波能量是波场中能量的主要组成部分。同时观察图11(b)可见，分离出的Scholte波，由直线的斜率可以计算得到波慢度为0.000 7221 s.m-1，每个检波器接收到Scholte波的时间以及Scholte波的波形与图4(b)吻合度较高，因此波场中的Scholte波被有效地提取出来。

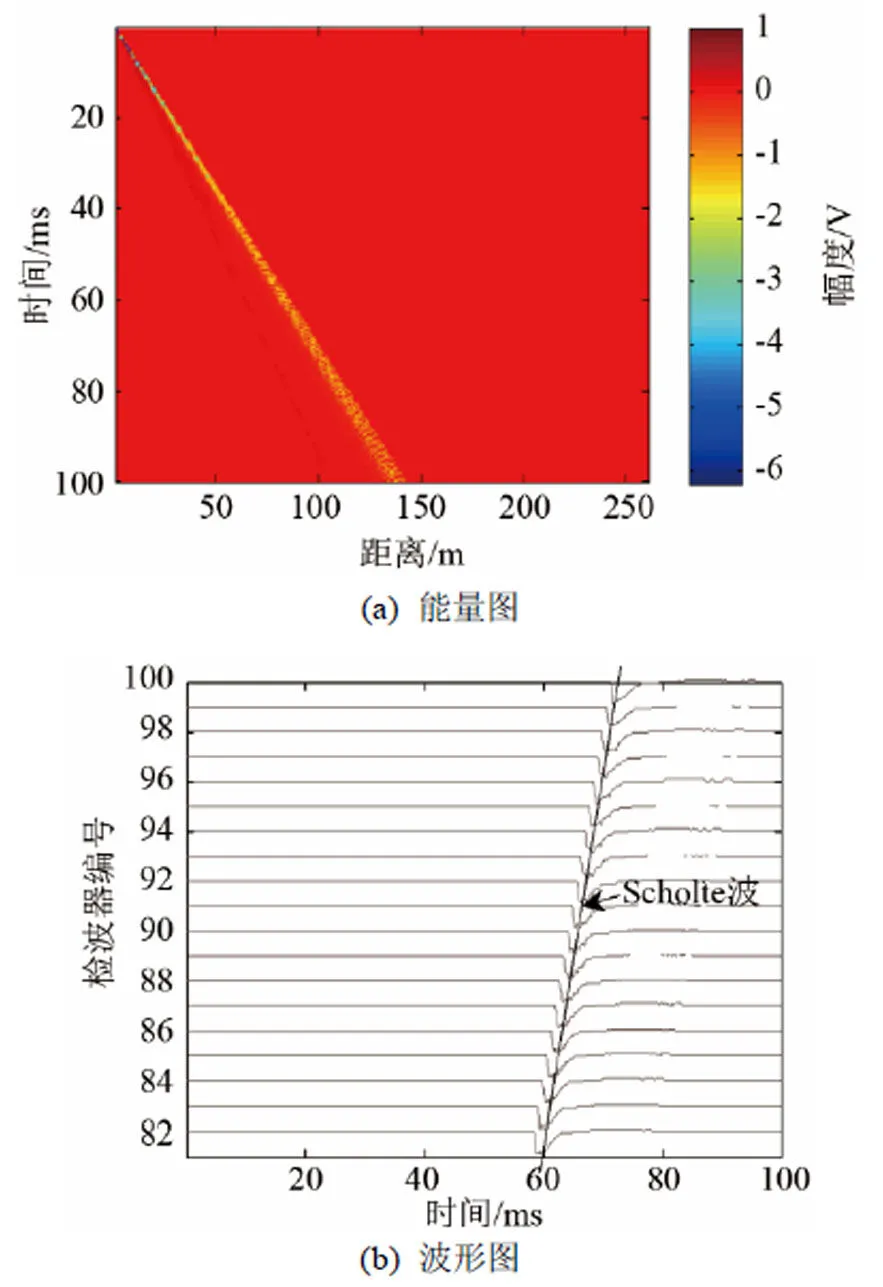
图11 在-域中的Scholte波

Fig.11 Scholte wave in-domain

3 结论

因为倾斜叠加原理的-变换法将球面波近似为平面波，所以本文的方法在很大程度上改善了变换的质量，但是并不能完全消除干扰。只有将点声源波场真正分解为平面波才能彻底解决问题，这也是下一步研究的方向。

[1] 卢再华, 张志宏, 顾建农. 舰船海底地震波形成机理的理论分析[J]. 应用力学学报, 2007, 24(1): 54-57.

LU Zaihua，ZHANG Zhihong，GU Jiannong．Theoretical analysis to mechanism of seafloor seismic wave induced by sailing vessel[J]. Chinese Journal of Applied Mechanics, 2007, 24(1): 54-57．

[2] 孟路稳, 程广利, 陈亚男, 等. 舰船地震波传播机理及其在水雷引信中的应用研究[J]. 兵工学报, 2017, 38(2): 319-325.

MENG Luwen, CHENG Guangli, CHEN Yanan, et al. On the mechanism of ship seismic wave and its application on the mine fuze[J]. ACTA ARMAMENTARII, 2017, 38(2): 319-325.

[3] 王朝令, 刘争平.-变换在隧道反射地震超前预报波场分离中应用的数值模拟研究[J]. 地球物理学进展, 2012, 27(5): 2216-2225.

WANG Zhaoling, LIU Zhengping. The modeling study of-transform applied in the tunnel seismic prediction[J]. Progress in Geophysics, 2012, 27(5): 2216-2225.

[4] 吴律.-变换及应用[M]. 北京: 石油工业出版社, 1993.

WU Lyu.-transformation and application[M]. Beijing: Petroleum Industry Press, 1993.

[5] 张军华. 地震资料去噪方法[M]. 东营: 中国石油大学出版社, 2011.

ZHANG Junhua. Seismic date denoising method[M]. Dongying: China University of Petroleum, 2011.

[6] 王周, 李朝晖, 龙桂华, 等. 求解弹性波有限差分法中自由边界处理方法的对比[J]. 工程力学, 2012, 29(4): 77-83.

WANG Zhou, LI Zhaohui, LONG Gui-hua, et al. Comparison among implementations of free-surface boundary in elastic wave simulation using the finite-difference method[J]. Engineering Mechanics, 2012, 29(4): 77-83.

[7] 秦臻, 任培罡, 姚姚, 等. 弹性波正演模拟中PML吸收边界条件的改进[J]. 地球科学-中国地质大学学报, 2009, 34(4): 658-664.

QIN Zhen, REN Peigang, YAO Yao, et al. Improvement of PML absorbing boundary conditions in elastic wave forward modeling[J]. Earth Science-Journal of China University of Geosciences, 2009, 34(4): 658-664．

[8] 张海刚. 浅海甚低频声传播建模与规律研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.

ZHANG Haigang. Research on modeling and rule of infrasound propagation in shallow sea[D]. Harbin: Harbin Engineering University, 2010.

Application of-transformation to extraction of the seabed Scholte wave excited by underwater sound source

WANG Ze-ming, CHENG Guang-li, MENG Lu-wen, LUO Xia-yun

(College of Electronic Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China)

Seismic wave field excited by underwater sound source is complex. In order to separate Scholte wave from seismic wave field, the original wave field is transformed from-domain into-domain by-transformation, and based on the characteristics of Scholte wave, which are different from those of other waves in-domain, the Scholte wave in-domain is extracted and then inversely transformed back to-domain to obtain the Scholte wave. Considering that the inherent false frequency effect and end port effect exist in-transformation, their formation mechanisms are analyzed theoretically, and then these two effects are suppressed by limiting wave slowness and adding time window respectively. The seismic field excited by underwater pulse sound source is given based on the high order staggered grid finite difference method, and then its wave components and characteristics are analyzed. Scholte wave in seismic wave field is extracted by using the above-mentioned method and the simulation results demonstrate the effectiveness of this method.

ship seismic field; extraction of Scholte wave;-transformation method; port effect; false frequency effect

TN911.7

A

1000-3630(2019)-01-0097-06

10.16300/j.cnki.1000-3630.2019.01.016

2018-01-13;

2018-02-27

国家自然科学基金(41576105)资助项目。

王泽明(1993－), 男, 山东诸城人, 硕士研究生, 研究方向为水声目标地声场。

程广利, E-mail: sonarcgl@126.com