OFDM水声通信系统动态OMP信道跟踪算法
戈俞峰,王彪
OFDM水声通信系统动态OMP信道跟踪算法
戈俞峰,王彪
(江苏科技大学电子信息学院,江苏镇江 212003)
针对正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)水声通信系统中最小二乘(Least Square, LS)信道估计算法和静态压缩感知信道估计算法分别存在估计精度低、导频开销大和计算复杂度高、实时性差的缺点,利用水声信道冲激响应的时域相关性,通过建立动态稀疏观测模型,提出一种动态正交匹配追踪(Dynamic Orthogonal Matching Pursuit, D-OMP)信道跟踪算法。该算法仅在初始时刻进行一次完整的正交匹配追踪(Orthogonal Matching Pursuit, OMP)信道估计获取信道支撑集,之后通过连续跟踪前一时刻信道支撑集的变化来跟踪信道。仿真结果表明,在导频开销相同的情况下,与传统LS算法、经典OMP算法相比,所提算法具有更好的信道跟踪性能和较低的算法复杂度。
水声通信;正交频分复用;信道跟踪;压缩感知
0 引言
目前,对水声通信的研究主要以点对点通信为主。由于正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术具有高频谱利用率和抗多途效应强的优点,因而在水声通信中得到了广泛的应用。水声OFDM信道估计也成为了一个研究热点。
其中最普遍的OFDM信道估计方法是基于导频的最小二乘(Least Square, LS)估计[1],由于LS算法复杂度低、易于实现,在工程上得到了广泛应用。但对于大多数的应用场合,浅海水声信道通常看作是一个缓慢时变的相干多途信道[2]。在此条件下,传统的LS算法由于需要插入大量导频,因此在连续跟踪信道状态信息时会降低系统的通信效率。随着压缩感知(Compressive Sensing, CS)理论的提出以及人们对水声信道稀疏性的认识,CS理论被逐渐应用到水声稀疏信道估计中[3-4],在提高信道估计精度的同时有效地减少了导频开销,提高了频谱利用率。尽管具有上述优越性,但CS方法由于重构算法的复杂度高,在跟踪缓慢时变水声信道时需要增加观测次数以提高精度,因此在实际工程中难以应用。
对此,近年来已有一些文献开始关注基于CS方法的缓慢时变信道的跟踪问题。文献[5]基于分布式压缩感知(Distributed Compressive Sensing, DCS)理论[6-7],利用一种同步正交匹配追踪(Simultaneous Orthogonal Matching Pursuit, SOMP)算法[8]对信道冲激响应(Channel Impulse Response, CIR)进行联合稀疏恢复,有效地降低了算法的复杂度,但该算法未考虑信道支撑集随时间的变化,因此与实际情况略有不符。文献[9]提出了一种将卡尔曼滤波与CS相结合的算法,成功地对缓慢时变稀疏信号进行了跟踪恢复。文献[10-12]则是文献[9]中算法的改进与应用。虽然此类基于卡尔曼滤波的CS算法均取得了优于传统方法的效果,但由于过高的算法复杂度,其实用性仍然较差。
针对上述问题,本文提出一种动态正交匹配追踪(Dynamic Orthogonal Matching Pursuit, D-OMP)信道跟踪算法。通过利用缓变水声信道支撑集缓慢变化的特点,所提算法仅需在初始时刻进行一次信道估计,之后在不同时刻只需跟踪信道支撑集的变化,计算新增路径和删除消失路径,而不需要每次都单独恢复信道支撑集。仿真实验表明,该算法具有比传统信道估计方法更高的估计准确度,算法复杂度也比传统CS方法更低,可以较好地跟踪缓慢时变水声信道。
1 信道与系统模型
1.1 缓变水声信道模型
考虑到浅海水声信道的多途衰落特性,本文采用抽头时延线模型描述水声信道的冲激响应(,),其表达式为[4]

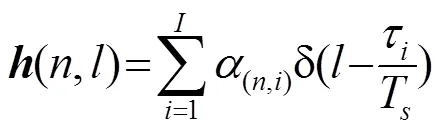
而对于时变水声信道,本文采用文献[14]中使用的基于自回归(Auto Regressive, AR)统计模型的方法对时变信道进行建模。根据式(2)对CIR的描述,时变水声信道可以用如下的一个复阶AR过程表示[14]:
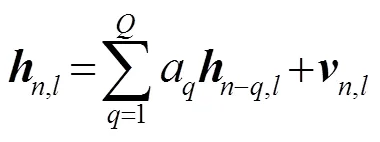

考虑到本文研究的缓变水声信道只需考虑相邻数据帧之间的信道变化,因此采用一阶AR过程即能满足要求,具体可表示为

其中,AR过程系数a和复高斯白噪声方差可根据Jakes模型计算Yule-Walker方程得到,具体结果可见于文献[14]。图1所示即为一阶AR过程建模的缓变水声信道在连续三个数据帧内的信道响应变化示意图,其中每个数据帧的长度至少为一个OFDM周期。
1.2 水声OFDM系统模型

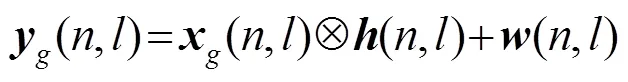




2 压缩感知(CS)信道估计

针对1.2节描述的SISO-OFDM系统,为使用CS方法进行信道估计,系统发送端插入随机导频。与上文介绍的频域信道估计不同,CS信道估计方法是基于导频的时域信道估计,因此式(8)的系统模型转化为如下形式:




3 基于D-OMP算法的信道跟踪
3.1 传统OMP信道估计算法及其分析
下面结合水声OFDM信道估计模型,给出OMP信道估计算法的具体步骤:
迭代过程:第次迭代

步骤2:更新索引集和重建原子集,即
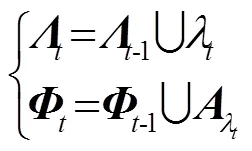
步骤3:利用LS算法计算CIR的估计值:

步骤4:根据CIR的估计值更新信号残差:

从上述步骤中可以看出,OMP算法在每次迭代中仅从过完备原子库中选取一个最匹配的原子来更新原子集合。而对于稀疏度的水声信道,至少需要进行次迭代才能精确恢复其CIR。随着迭代次数的增加,运算时间也相应地大幅增加,这就是OMP算法实时性差的原因。对于本文讨论的缓变水声信道,由于相邻帧之间的CIR具有时域相关性,即大系数多径的时延位置基本不变,幅值随时间发生较快改变。对此,可以考虑将前一帧内CIR的支撑集作为当前帧内信道响应的初步支撑集,然后判断有无新增路径和消失路径,这样就避免了在每一帧内都进行次迭代来恢复CIR,有效减少了算法的复杂度。
3.2 D-OMP信道跟踪算法及其门限阈值选取
水声信道跟踪需要接收端进行持续观测,经典CS方法均建模为单观测矢量模型。本文在多观测矢量模型的基础上,结合前文中一阶AR过程建模的时变稀疏信道来阐述D-OMP算法。
假设发送端连续发送帧数据,则式(13)的单观测模型可改写为如下的多观测形式:


基于此观测模型,下面是D-OMP信道跟踪算法的具体步骤:

步骤1:根据上一时刻CIR的估计值更新信号残差:


步骤3:更新索引集和重建原子集,即

步骤4:利用LS算法计算CIR的估计值:
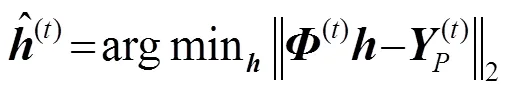
步骤5:判断是否满足路径消失条件:

若满足,删除消失路径并更新支撑集:
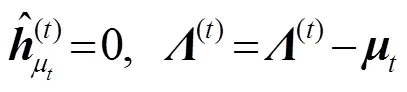

考虑一帧内的信道估计,将式(13)改写为如下形式:


其次是等效噪声向量中任意元素的方差:
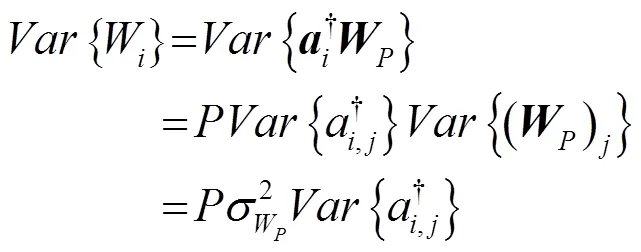

结合以上分析,式(29)所示的等效噪声方差可进一步表示成式(31)的形式:
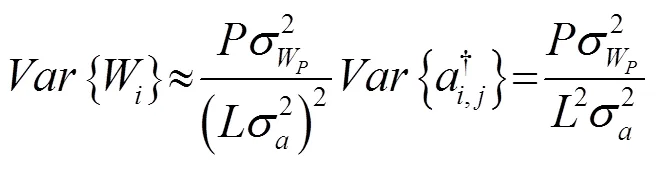
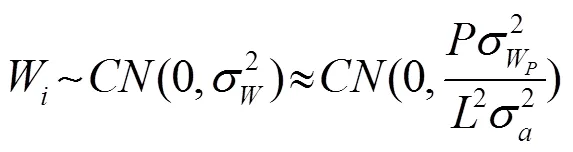


4 仿真与分析
4.1 参数设置
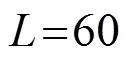

表1 OFDM系统仿真参数
4.2 结果分析
为方便评估各种信道估计算法的性能,本文采用归一化均方误差(Normalized Mean Square Error, NMSE)[16]、误符号率(Symbol Error Rate, SER)以及CPU运行时间作为算法性能的评价指标。其中,归一化均方误差的定义为:
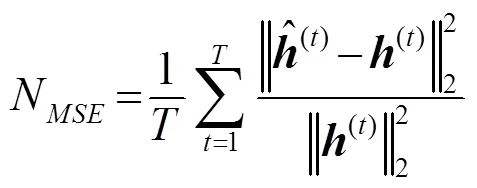

而对于SOMP算法,由于其利用相邻帧之间信道多径的稀疏相关性对水声信道进行联合稀疏恢复估计,因此性能得到了极大提高。但该算法的理论基础是DCS理论下的联合稀疏模型2(Joint Sparsity Model 2, JSM2[5])模型,在该模型下不同时刻的信道都具有相同的稀疏支撑集,而在仿真中,由于模拟了信道支撑集的缓慢变化,即不同时刻存在新增路径和消失路径。因此,图2、3的仿真结果中,SOMP算法的性能比本文所提D-OMP算法略低。

图 2 不同信噪比下的NMSE性能比较

图 3 不同信噪比下的SER性能比较
此外,在本次仿真中还使用了Genie-KF算法[17]作为对比。Genie-KF是接收端已知各时刻信道支撑集的卡尔曼估计,由于已知先验信息,因此可以认为是估计误差最小的均方误差估计,其性能优于所有未知先验信息的信道估计算法,可以看作是所有算法的理论极限。从图2、3中也能看出,所有算法与它相比均有差距,但D-OMP算法差距最小。
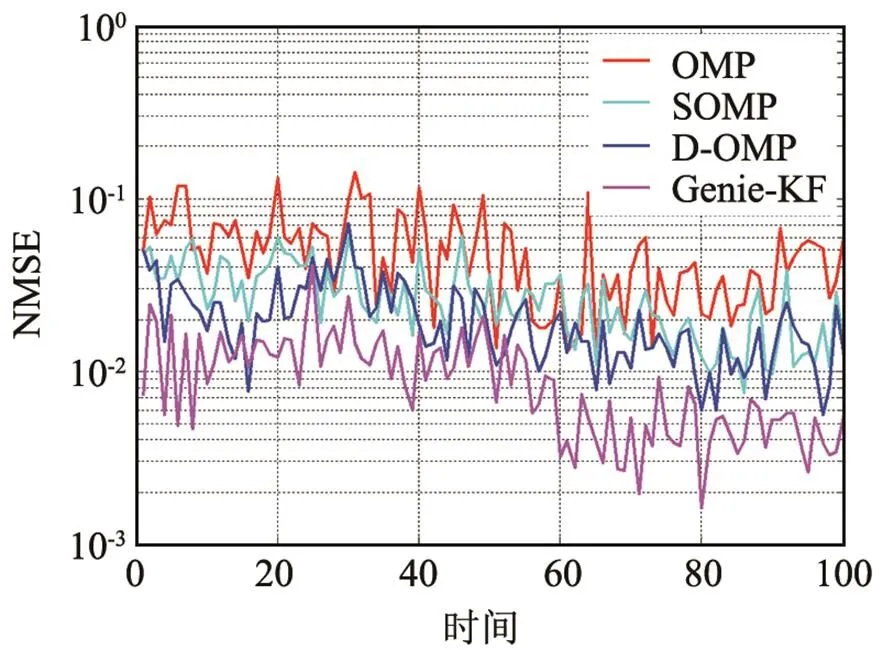
图 4 不同时间下的NMSE性能比较

最后是各种算法的CPU运行时间的比较与分析。仿真所使用的MATLAB版本为2014a,所在计算机的CPU型号为Intel奔腾双核G2030,主频3.0 GHz,内存4.0 GB。仿真共进行6次,在信噪比5~30 dB范围内每隔5 dB进行一次,每次发送端均发送100帧数据(即100个OFDM符号),接收端对这100帧数据进行解调,计算CPU所需的运行时间,6次仿真后取其平均值即为CPU平均运行时间,具体仿真结果如表2所示。

表2 不同算法的CPU平均运行时间
从表2中可以看出,本文所提D-OMP算法的CPU平均运行时间与LS算法相当,虽高于SOMP算法,但优于对比的OMP和Genie-KF算法,仍具有较高的信道跟踪速度。SOMP算法由于默认各时刻信道支撑集相同,因此只需进行一次信道支撑集的恢复,极大地降低了算法复杂度。与之形成对比的是,经典静态OMP信道估计算法,在每一帧内都需要进行完整的信道支撑集恢复,造成较长的CPU运行时间。至于Genie-KF算法,与所有基于卡尔曼滤波的信道估计算法类似,虽具有不错的信道估计准确度,但算法复杂度太高,不适用于实时性要求较高的场合。
5 结论
考虑到浅海水声信道的冲激响应具有稀疏性和缓慢时变特性,本文利用相邻帧之间水声信道的时域相关性,提出一种适合于浅海缓慢时变信道的动态正交匹配追踪信道跟踪算法。仿真结果表明,在对信道的持续跟踪过程中,本文所提算法不仅弥补了传统LS算法估计精度和频谱利用率低的问题,还有效地克服了经典静态CS算法复杂度高、实时性差的缺点,并且与现有同类CS算法相比,也有更好的性能。
[1] 宁小玲, 张林森, 梁玥. 一种改进LS信道估计算法在稀疏多径水声信道中的应用[J]. 声学技术, 2016, 35(4): 378-384.
NING Xiaoling, ZHANG Linsen, LIANG Yue. Application of an improved LS channel estimation algorithm to sparse multipath underwater acoustic channel[J]. Technical Acoustics, 2016, 35(4): 378-384.
[2] 乔钢, 王巍, 王玥, 等. 基于压缩感知的OFDM水声通信信道二次估计算法[J]. 声学技术, 2013, 32(5): 357-361.
QIAO Gang, WANG Wei, WANG Yue, et al. The complex channel estimation based on compress sensing in OFDM via underwater acoustic channel[J]. Technical Acoustics, 2013, 32(5): 357-361.
[3] GUO S C, HE Z Q, JIANG W P, et al. Channel estimation based on compressed sensing in high-speed underwater acoustic communication[C]//IEEE 9th International Conference on Information, Communications and Signal Processing, 2013: 1-5.
[4] BERGER C R, ZHOU S L, PREISIG J C, et al. Sparse channel estimation for multicarrier underwater acoustic communication: From subspace methods to compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1708-1721.
[5] WANG D H, NIU K, BIE Z S, et al. A new channel estimation method based on distributed compressed sensing[C]//IEEE Wireless Communications and Networking Conference, 2010: 1-4.
[6] GONG B, QIN Q, REN X, et al. Distributed compressive sensing based doubly selective channel estimation for large-scale MIMO systems[J]. Mathematics, 2015, arXiv: 1511.02592v1 [cs.IT].
[7] GONG B, LIN G, QIN Q, et al. Block distributed compressive sensing based doubly selective channel estimation and pilot design for large-scale MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 9149-9161.
[8] 周跃海, 曹秀岭, 陈东升, 等. 长时延扩展水声信道的联合稀疏恢复估计[J]. 通信学报, 2016, 37(2): 165-172.
ZHOU Yuehai, CAO Xiuling, CHEN Dongsheng, et al. Jointing sparse recovery estimation algorithm of underwater acoustic channels with long time delay spread[J]. Journal on Communications, 2016, 37(2): 165-172.
[9] VASWANI N. Kalman filtered compressed sensing[C]//IEEE 15th International Conference on Image Processing, 2008: 893-896.
[10] WANG D H, NIU K, HE Z Q, et al. Pilot-aided channel estimation method based on compressed sensing and Kalman filtering in OFDM systems[C]//IEEE International Conference on Wireless Information Technology and Systems, 2010: 1-4.
[11] DING X, CHEN W, WASSELL I. Sparsity-fused Kalman filtering for reconstruction of dynamic sparse signals[C]//IEEE International Conference on Communications, 2015: 6675-6680.
[12] GAO Y, XU K, CHEN Y. A novel method of multi-band spectrum sensing exploiting dynamic compressive sensing[C]//IEEE 13th International Conference on Signal Processing, 2016: 1152-1156.
[13] 叶新荣, 朱卫平, 孟庆民. 基于SAMP重构算法的OFDM系统稀疏信道估计方法[J]. 信号处理, 2012, 28(3): 392-396.
YE Xinrong, ZHU Weiping, MENG Qingmin. SAMP construction based sparse channel estimation for OFDM systems[J]. Signal Processing, 2012, 28(3): 392-396.
[14] CHEN B H, CUI Q M, YANG F, et al. A novel channel estimation method based on Kalman filter compressed sensing for time-varying OFDM system[C]//IEEE 6th International Conference on Wireless Communications and Signal Processing, 2014: 1-5.
[15] 张晓东, 董唯光, 郭俊锋, 等. 基于变换的压缩感知风电变流器电压信号压缩方法[J]. 广西大学学报(自然科学版), 2016, 41(6): 1855-1862.
ZHANG Xiaodong, DONG Weiguang, GUO Junfeng, et al. Wind power converter voltage signal compression method of compressed sensing based ontransform[J]. Journal of Guangxi University(Natural Science Edition), 2016, 41(6): 1855-1862.
[16] 刘政, 刘本永. 基于图像深度信息的尺度不变特征变换算法误匹配点对剔除[J]. 计算机应用, 2014, 34(12): 3554-3559.
LIU Zheng, LIU Benyong. Removal of mismatches in scale-invariant feature transform algorithm using image depth information[J]. Journal of Computer Applications, 2014, 34(12): 3554-3559.
[17] LI H, GUO W B, SUN Z, et al. Adaptive Kalman filtered compressive sensing for streaming signals[C]//IEEE 78th Vehicular Technology Conference, 2013: 1-5.
Dynamic OMP channel tracking algorithm for OFDM underwater acoustic communication systems
GE Yu-feng, WANG Biao
(School of Electronic and Information, Jiangsu University of Science and Technology, Zhen Jiang 212003, Jiangsu, China)
For the OFDM underwater acoustic communication systems, the least square (LS) channel estimation algorithm has the disadvantages of low estimation accuracy and high pilot overhead, while the static compressive sensing channel estimation algorithm has the disadvantages of high computational complexity and poor real-time performance. Aiming at these problems, a new algorithm called dynamic orthogonal matching pursuit (D-OMP) is proposed by establishing a dynamic sparse observation model based on the temporal correlation of the underwater acoustic channel impulse response. The algorithm only performs a complete OMP channel estimation at the initial time to obtain the channel support set, and then tracks the channel by continuously tracking changes in the previous channel support set. The simulation results show that the proposed algorithm has better channel tracking performance and lower algorithm complexity compared with the traditional LS algorithm and the classical OMP algorithm under the same pilot overhead.
underwater acoustic communication; orthogonal frequency division multiplexing(OFDM); channel tracking; compressive sensing
TN929.3
A
1000-3630(2019)-01-0051-07
10.16300/j.cnki.1000-3630.2019.01.008
2017-07-26 ;
2017-10-25
国家自然科学基金项目(11574120、61401180、U1636117);江苏省自然科学基金项目(BK20161359)
戈俞峰(1993-), 男, 江苏苏州人, 硕士研究生, 研究方向为水声通信、水声信号处理。
戈俞峰, Email: geyufg@163.com

