强鲁棒性和高锐化聚集度的BGabor-NSPWVD时频分析算法

郝国成 谈帆 程卓 王巍 冯思权 张伟民

时频分析(Time-frequency analysis,TFA)是从时间–频率的角度来处理非平稳信号的方法,其基本思想是建立时间和频率的联合函数,描述信号在时间–频率平面的能量密度或强度[1−2].它将信号从时间域变换到时间–频率联合域,不同频率分量的时间关联特性能够在时–频平面上有效地表示出来.信号在任意时刻的能量都聚集在此瞬时频率附近,基于线性方法的逆变换则可以重构其等效的时间域信号[3].目前时频分析方法已经广泛应用于自动化控制、信号处理、数据通信、地质勘探、基础物理、工业生产等各个领域[4−5].在合成人造金刚石加工环节,自动检测顶压机顶锤是否破裂是该项生产过程的重要步骤之一,可有效降低人工凭经验听音辨别的误差.该金属破裂信号属于典型的非平稳信号,利用合适的时频分析方法能够对此类信号进行有效的时频表示,针对信号的破裂局部信息给出对应的高幅值频率分布,为数据采集卡的频率判别窗口提供阈值依据.本文提出基于二值化Gabor的归一化Wigner-Ville分布(Wigner-Ville distrivution,WVD)和归一化伪平滑WVD(BGabor-NWVD,BGabor-NSPWVD)时频分析算法,具有良好的高锐化时频聚集度和鲁棒性,对金属破裂样本信号有较好的去噪效果,可以得出有参考意义的时间和频率联合分布.

1 时频分析

时频分析通过设计时间和频率的幅度或能量密度关联函数,将一维的时间序列信号以二维的时间–频率密度函数形式表示,旨在揭示信号中包含多少频率分量,以及每一分量随时间的变化规律.时频分析方法可以分为线性型时频表示、非线性型时频表示和二次型时频表示.1)典型的线性时频表示有短时傅里叶变换(Short-time Fourier transform,STFT)[6−7]、S 变换(S transform,ST)[8]、和小波变换(Wavelet transform,WT)[9]等,线性时频表示会受到不确定性原理的制约,存在时频模糊等问题.2)非线性型时频表示包括基于经验模型分解(Empirical mode decomposition,EMD)的希尔伯特–黄变换 (Hilbert-Huang transformation,HHT)[10]、集合经验模型分解(Ensemble empirical mode decomposition,EEMD)及其改进算法[11−12]、同步压缩变换(Synchrosqueezing transform,SST)[13]等.基于EMD和EEMD的HHT具有良好的窄带自适应性,但缺乏严谨的数学支撑,且信号频率带宽较大时,其时频聚集度有待提高.SST方法是Daubechies于2011年提出的一种时频重排技术,其变换核可以基于小波变换或者基于STFT变换,SST支持信号重构,其时频输出具有高锐化聚集度的特点[13],但直接SST存在复杂频率成分交叉点附近的描述模糊和鲁棒性弱的缺点.改善SST的鲁棒性,可采用与压缩感知稀疏方法[14]相结合的方法,此部分本文作者另有相关文章阐述.3)二次型时频分布则是一种更为严格的时频表示,能够描述信号的瞬时功率谱密度,可从时间–频率–能量三者联合分布的维度来了解信号的特点.二次型时频分布一般包括Cohen类时频分布[6]、WVD[15],以及对WVD方法的改进,如STFT-WVD[16]、STFT-SPWVD[17]和NSTFT-WVD[18]等.

常用的STFT方法由Gabor于1946年提出[7],即加窗的傅里叶变换.窗函数可以选择矩形窗、三角窗、汉宁(Hanning)窗、海明(Hamming)窗、布拉克曼(Blackman)窗、恺撒(Kaiser)窗等,当STFT的窗函数选择高斯窗时,加窗短时傅里叶变换称为Gabor变换.根据Heisenberg测不准原理,高斯函数窗口面积已达到测不准原理下界,是时域窗口面积达到最小的函数,Gabor变换是最优的STFT.文献[19]采用稀疏分析窗的方法来求解离散Gabor变换,一定程度提高了时频的聚集度.STFT和Gabor变换使用的是大小和形状固定的滑动窗口,变换基函数为非正交系,对于突变和非平稳信号,不能精确分解周期比时间窗大的低频信号,且高频的时频分辨率比较差,需要辅以其他高时频聚集度方法加以改进,WVD就是较好的选择,该方法具有理论上最高时频分辨率和许多优良的数学性质.

WVD是一种基础并且重要的二次型时频分布,具有较高的时频聚集度,应用广泛.Wigner分布在1932年被提出,并应用于量子力学,但没有引起重视,直到Ville在1948年将它应用于信号分析领域,并称之为Wigner-Ville分布,开始了它的快速发展时期.尤其自上世纪八十年代以来,陆续发表了相当数量的WVD论文,对WVD的定义、性质、时频表示、各种改进进行了大量的讨论,以其良好的时变特性,特别是可直接由其精确定义“瞬时频率”而广泛用于非平稳信号的分析.同时需要注意的是,这种方法虽然对边缘特性、瞬时频率和局域刻画等都有很好的描述,其时频图上的频率成分有高锐化的聚焦,但WVD不满足叠加原理,其变换过程中产生新的频率交叉项分量成为该方法的瓶颈[18].交叉项的存在使得时频图上的分布混乱,额外产生大量的噪声成分,充斥在真实频率之间,干扰对信号的识别分析,极大地限制了WVD分布的实际应用.

综上所述,采用Gabor与WVD结合对非平稳信号进行时频分析,可发挥各自的极限优点,去除WVD交叉项的同时,得到较高的局部时频分辨率,满足对非平稳信号进行时频分析的高锐化时频聚集度和强鲁棒性要求.本文对Gabor和WVD分别进行改进后再结合,提出BGabor-NWVD和BGabor-NSPWVD算法,同时兼顾线性时频表示与二次型时频表示的优点,能够获得较好的时频聚集度、消除WVD交叉项干扰、抑制噪声,并具有强鲁棒性,同时能在金属破裂样本信号的时频分析中有较好的应用.

2 BGabor-NWVD和BGabor-NSPWVD

2.1 Gabor与WVD的优缺点

STFT与Gabor变换是常用的时频分析方法之一.其优点是,对信号具有一定程度的自适应性,能够如实还原输入信号的时频分布,对信号的低频和高频两端都有较为一致的局部描述,得到的非平稳信号的时频分布较为平滑,分析多分量信号的时候,没有交叉项的虚假频率成分干扰.STFT变换的定义如式(1),把STFT的窗函数变为高斯函数,就得到式(2)的Gabor变换[7].

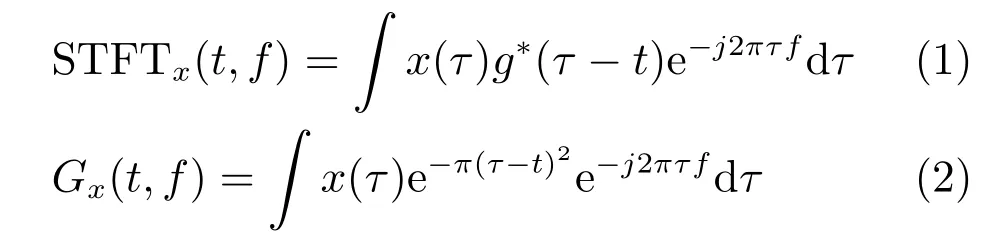
Gabor的时频分辨率由窗函数g(τ−t)的时域大小直接决定,一旦窗口函数选定,其时频分辨率就已确定,不随时间和频率的变化而变化.为了提高时间分辨率,窗函数的时间宽度应该尽量短,但为了提高频率分辨率,窗函数的时间宽度则应尽可能长,受不确定性原理的约束,时间分辨率和频率分辨率是一对矛盾体.在处理非平稳信号的过程中,对于高频信息,需要用较窄的窗函数进行分析,而对于低频信息,则需要用较宽的窗函数进行分析.而Gabor的窗函数确定以后,只能以一种固定分辨率进行时频分析,无法兼顾高频信息和低频信息[20−21].这种方法的缺点很明显,其时频聚集性不佳,局部的频带粗糙,难以精确显示时频特点,如图1所示,需要通过其他方法提高其时频聚集度.

WVD是最基本且严格的时间和频率二维联合函数,可以看作信号在时间和频率平面上的能量密度解.虽然时频表示的线性特性是我们所希望具备的重要特性,但因为能量本身就是一种二次型表示,因此,当反映信号的时间–能量分布时,采用WVD这样的二次型时频分布则更加合适.WVD属于Cohen类双线性时频分布的一种,可在时域和频域同时揭示信号的能量分布,并且其物理意义明确.近年来,凭借着其优越的时频聚集性,WVD被广泛应用于信号分析和处理领域,尤其在非平稳信号的瞬时频率估计、信号的相干检测和时变滤波等诸多领域,是最常用的双线性时频分布之一.WVD分布定义为:

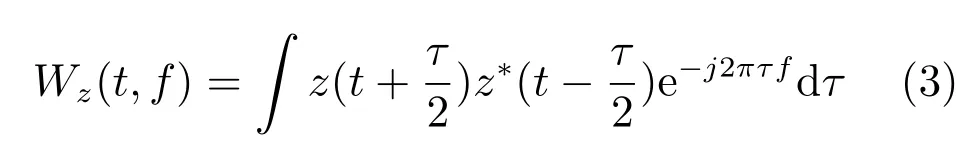
其中,z(t)为目标信号的解析信号,τ是积分变量,t是时移,f是频率.式(3)没有使用窗函数,避免了线性时频表示时间和频率分辨率相互制约的矛盾.WVD的时间带宽积达到了不确定原理给出的下界,可以呈现较其他时频分布更好的时频聚集特性.但WVD在处理复杂信号,尤其是频率相近的加性信号的时候,由自身变换过程所引入的交叉项问题同样很严重.设z(t)=z1(t)+z2(t),则z(t)的WVD如式(4).

图1 信号f1的理想时频、Gabor和WVD对比图Fig.1 Ideal time-frequency spectrum,Gabor,WVD off1

其中,等号右边的Wz1(t,f)与Wz2(t,f)分别为z1(t)和z2(t)的WVD,即变换所要求解的时频信息项,第3项2Re{Wz1,z2(t,f)}为交叉项.由式(4)可知,两个信号和的WVD并不等于它们各自WVD之和,交叉项的存在给WVD的应用带来不小的困扰.

式(5)是信号f1(t)的时域表达式,图1为信号f1(t)理想时频表示图、Gabor和WVD的时频分布图.从图中可以看出,Gabor变换的时频分辨率不高,而WVD方法的分辨率尽管略高于Gabor变换,但存在严重的交叉项干扰问题.因此,单独的Gabor和WVD都不理想,需要进行一定的改进,以克服时频分辨率和交叉项的影响.

2.2 Gabor与WVD的结合思想

Gabor-WVD变换的基本思想是利用Gabor和WVD各自的优点,通过两者重叠运算来增强Gabor和WVD信息项,抑制由WVD变换产生的交叉项部分,以达到Gabor-WVD变换在保持良好的时频聚集特性的同时,具有消除交叉项的效果.Gabor-WVD变换定义了G(t,f)与W(t,f)这两个过程变量,其任意函数表达式如式(6)所示[18].

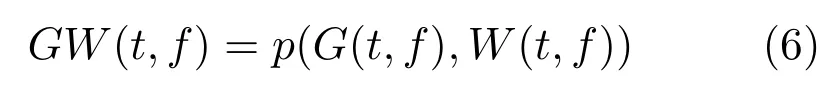
其中,p(x,y)为任意函数,例如当p(x,y)=xayb时,GW(t,f)=Ga(t,f)Wb(t,f);当p(x,y)=x+y时,GW(t,f)=G(t,f)+W(t,f).Gabor-WVD得出的结果可以很好地描述非平稳信号的二维时频分布,并且具有良好的聚集性,对于WVD产生的交叉项也有较好的抑制.但本文作者在文献[18]中已经明确,STFT-WVD不能真实反映信号的三维幅值,如本文第三部分的数值实验仿真例子所示.Gabor-WVD的三维输出时频表示存在较大的误差和干扰,具体体现在信息项上的交叉项无法消除.针对交叉项和三维幅值不能正确显示的问题,需要对Gabor-WVD进一步改进.由于交叉项成因与变换过程中的两个乘项表现为时频轴上的频率相邻与中间频段位置的量[18],因此,消除交叉项的思路,可采用设定阈值来清除指定频段上的虚假分量,或是利用其他合适的数值进行替代,或是对该项增添幂指数进行消除.实现Gabor-WVD的若干种方法如式(7)～(9).

根据函数p(x,y)形式的不同,GW(t,f)的运算方式也有所不同.由于式(7)只取Gabor变换与WVD后的数值中的较小值,故称为最小值法.式(8)将c设置为交叉项消除阈值,对Gabor数组中的部分特定数据取0或1,故称为二值化法.式(9)设置a、b为幂指数,通过幂指数来消除交叉项,故称为幂调节系数法.

2.3 BGabor-NWVD和BGabor-NSPWVD

尽管Gabor-WVD方法能够有效消除WVD产生的虚假分量,但并不能消除叠加在信息项上的分量.针对此问题,本文对Gabor和WVD同时进行改进,提出BGabor-NWVD和BGabor-NSPWVD算法.BGabor-NWVD算法的步骤为:

步骤1.首先各自对输入信号进行Gabor和WVD变换,分别得到数组A和数组B.

步骤2.根据时域波形的幅度,对Gabor数组进行二值化处理(Binarization),得到数组Gabor1,同时,根据WVD绝对值数组中的最大值对WVD数组进行归一化处理(Normalization),得到数组WV D_1.

步骤3.两数组进行点除,得到新的临时数组Y,根据其本身的大小,设置阈值K1、K2.

步骤4.修正点除后的结果数组B,记录数组Y中大于K1的位置,在数组B中将相同位置的元素置0,得到数组B0.

步骤5.对数组Y进行修正,将数组Y中大于K1的元素置1,将数组Y中小于K2的元素也置1,得到新数组Y0.

步骤6.数组B0点除Y0,输出BGabor-NWVD数组,算法结束.

数值实验结果表明,这一改进算法对信息项上交叉项的叠加有较好的抑制效果.SPWVD是对WVD的一种加窗平滑改进,SPWVD本身即具有消除WVD交叉项的作用,将BGabor与SPWVD相结合,也取得了较好的效果.需要特别说明的是,与SPWVD结合后,尽管牺牲了一定的二维时频聚集度,但大幅度提高了非平稳信号三维时频表示的准确度.BGabor-NSPWVD算法流程与BGabor-NWVD算法类似,将信号的WVD换成SPWVD即可,BGabor-NWVD变换算法流程框图如图2所示.

3 数值仿真实验

3.1 时频分布对比

本节采用2个构造函数来进行多个时频分析方法的测试实验,重点讨论每种方法的时间和频率聚集度,以及每个频率分量的幅值分布是否正确.构造的2个函数属于易产生交叉项的多频分量信号,如式(10)和式(11),分别为较为复杂的四分量线性调频信号和三分量正弦频率信号,数值实验的方法采用STFT、WVD、SPWVD、Gabor-WVD、Gabor-SPWVD、BGabor-NWVD和BGabor-NSPWVD.图3为三分量和四分量构造函数的二维时频图,采用本文改进后的BGabor-NWVD和BGabor-NSPWVD,可以看出,这两种方法都能准确地显示函数的时频分布,没有交叉项的干扰,且时间–频率轴都有较好的聚集度.在进行BGabor-NWVD和BGabor-NSPWVD处理时,同时比较使用最小值法、二值化法和幂指数调节法实现Gabor-WVD和Gabor-SPWVD的结果,讨论各方法的三维幅值分布是否准确.线性调频四频率分量信号表示如式(10)所示,m为一般参数,可以根据需要调整,这里选取m=0.2.

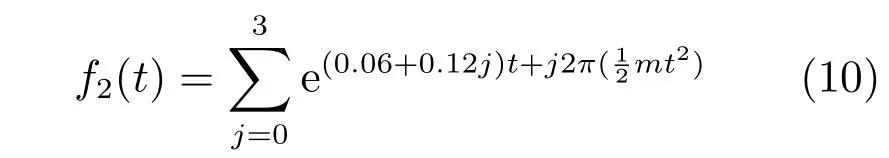
正弦三频率分量信号如式(11)所示.

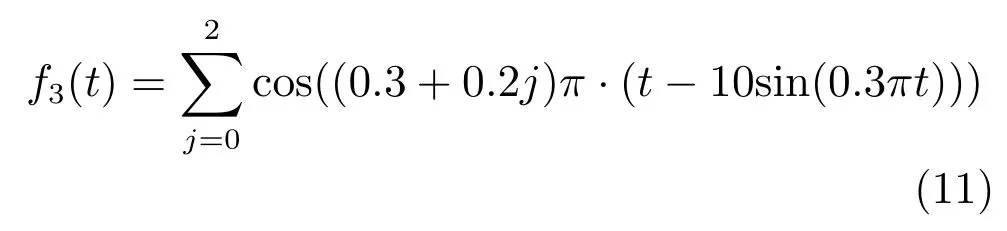
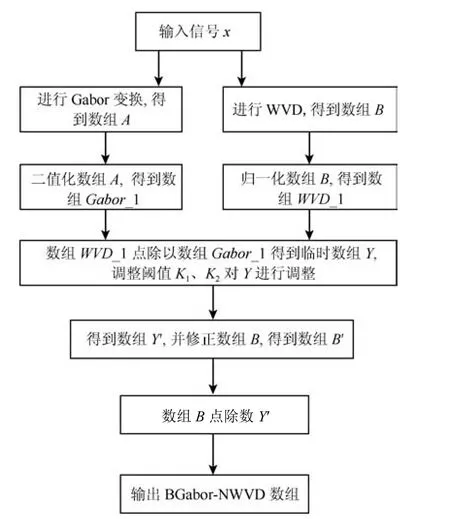
图2 BGabor-NWVD算法流程图Fig.2 BGabor-NWVD algorithm flow chart

图3中,BGabor-NWVD 和BGabor-NSPWVD方法都能较好地实现复杂信号的二维时频分布,消除了交叉项的干扰,BGabor-NWVD较BGabor-NSPWVD的二维时频聚集度略好,采用NSPWVD方法牺牲了少许的平面聚集性,但这并不影响时频表现和分布的判断.下面讨论这些方法的时频三维分布情况,首先看基本的Gabor、WVD及WVD的改进SPWVD,如图4所示.

图3 四分量f2和三分量f3的二维时频图Fig.3 Two-dimensional time-frequency diagram of four components signalf2and three components signalf3

图4为函数f2的Gabor、WVD和SPWVD方法得到三维时频分布图,其中,图4(a)中的Gabor方法没有交叉项,但是底端呈扩散状分布,频率聚集性差;图4(b)中WVD的交叉项干扰严重;图4(c)中SPWVD没有交叉项,但是频率项上的幅度有尖端失真,需要予以消除.

3.2 BGabor-NWVD

针对图4出现的问题,采用二值化改进的Gabor与WVD、SPWVD相结合的算法,时频分析三维效果如图5所示.

将Gabor与WVD直接相结合,按照式(7)～(9)分别进行Gabor-WVD最小值法、二值化法和幂系数调节法的三维时频分布画图,如图5(a)、5(b)和5(c)所示,3个图中函数f2和f3的频率分量幅度出现了较大失真.由此需要对Gabor-WVD算法进一步改进,先将Gabor二值化(BGabor),再结合归一化的WVD(NWVD),得到BGabor-NWVD算法.实验仿真函数f2和f3的三维时频分布如图5(d),较好地克服了Gabor-WVD方法的幅值失真问题,其幅值顶端依旧存在模糊现象,还需要进一步加以改进.

图4 四分量f2的三维时频图Fig.4 Three-dimensional time-frequency diagram of four components signalf2

图5 基于Gabor和WVD的四分量f2(上)和三分量f3(下)的三维时频比较图Fig.5 Three-dimensional time-frequency diagram of four-componentsf2(upper)and three-componentsf3(bottom)based on Gabor and WVD

3.3 BGabor-NSPWVD

SPWVD具有较好地平滑效果,考虑将Gabor与SPWVD相结合,可以进一步优化幅值模糊现象,如图6所示.

Gabor与SPWVD相结合,可以很大程度上平滑信号的幅度数值,使其时频表现更接近真实的各频率分量幅度.但图6中,图6(a)、6(b)和6(c)的幅度仍然存在一些干扰和噪声分量,其中,图6(a)幅度顶端较好,但是幅度的底端范围较宽,出现能量泄漏现象.图6(d)的BGabor-NSPWVD算法效果最佳,幅度刻画良好,仿真函数f2和f3各分量的顶端和低端没有出现明显失真,时间–频率–幅度分布清晰准确.BGabor-NSPWVD和Gabor-NWVD算法都能去除信息项上的叠加残余,对交叉项有较好地抑制效果.两种算法相比较,BGabor-NSPWVD对信号分量在时频平面的幅度还原效果更优于Gabor-NWVD,其时间–频率–幅度的三维分布具有良好的表现能力.

4 鲁棒性实验

4.1 二维时频分布对比

BGabor-NWVD和BGabor-NSPWVD算法不仅对复杂信号的交叉项有较理想的消除作用,而且对附着在信号上的高斯白噪声同样有较强的抑制效果,两种算法在时频分析处理效果上具有强鲁棒性的特点,利于处理实际的含噪信号.构造具有多频分量的实验仿真信号,加入−10dB至20dB的高斯白噪声,对比Gabor、WVD、SPWVD、Gabor-WVD、Gabor-SPWVD、BGabor-NWVD和BGabor-NSPWVD方法的二维时频分析效果.由于篇幅限制,本文仅列出加入2dB噪声时函数f4的二维时频分布,如图7所示.

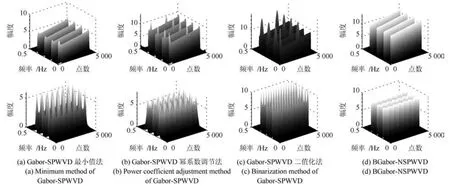
图6 基于Gabor和SPWVD的四分量f2(上)和三分量f3(下)的三维时频比较图Fig.6 Three-dimensional time-frequency diagram of four-componentsf2(upper)and three-componentsf3(bottom)based on Gabor and SPWVD

图7 含噪信号f4的二维时频分布比较(SNR=2dB)Fig.7 The two-dimensional time-frequency distribution of the noisy signalf4(SNR=2dB)

图7(b)为改进前的Gabor方法,即高斯变换核STFT,时频聚集度较差且噪声分布干扰严重.图7(c)的WVD方法存在严重的交叉项干扰,需要去除存在于真实频率之间的虚假频率分量.图7(d)的SPWVD较好地去除了交叉项和噪声干扰,但是由于采用伪平滑的手段,使得该方法的时频聚集度较差.图7(e)、7(f)和7(g)是结合后的Gabor-WVD方法,其中幂系数调节法去除交叉项的效果略好,但是这三种方法对噪声的抑制和去除交叉项都不满足要求.图7(h)采用进一步结合后的BGabor-NWVD方法,较好地去除了交叉项和噪声干扰,具有最佳的二维时频分布表现.

图7(i)、7(j)和 7(k)是 Gabor与 SPWVD相结合的三种方法,对交叉项的抑制尚可,但对噪声干扰的去除效果还需提高.图7(l)为BGabor-NSPWVD方法,对交叉项的抑制和噪声的去除都较为理想,时频聚集度略逊于图7(h)的BGabor-NWVD方法,但是对交叉项的抑制和鲁棒性而言,BGabor-NSPWVD和BGabor-NWVD都是可以采用的方法.

4.2 时频聚集度评价

文献[20]给出了评价时频聚集度的量化公式,如式(12),n为时间窗长度,ω为频率,式(12)通过调整窗口参数,求得最大的时频分布的第四幂范数与第二幂范数之商来评价时频聚集度.向实验函数f4添加−10dB至20dB的高斯白噪声,求解函数f4的EJP数值,用以衡量各个方法的聚集度分布,如表1所示.将表1的数值用图8的折线趋势来表示,能够较为直观地比较每种方法的聚集度效果.

时频聚集度评价图8中,信噪比(SNR)大于0dB时,BGabor-NWVD和BGabor-NSPWVD方法的聚集度EJP开始平稳,且其值高于其他方法,随着SNR的变化,这两种改进算法皆具有较高的时频聚集度和强鲁棒性,BGabor-NWVD的聚集度优于BGabor-NSPWVD算法,与图7的二维时频分布效果图一致.

5 硬质合金顶锤破裂信号监测

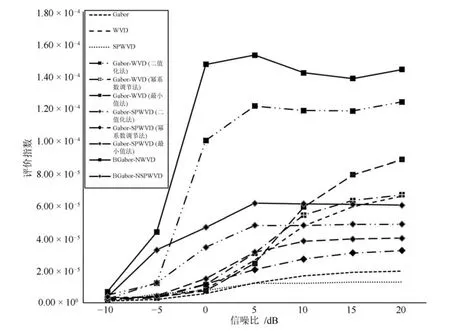
图8 时频聚集度参数EJP评价比较Fig.8 Comparison of time-frequency aggregation degree evaluation onEJP

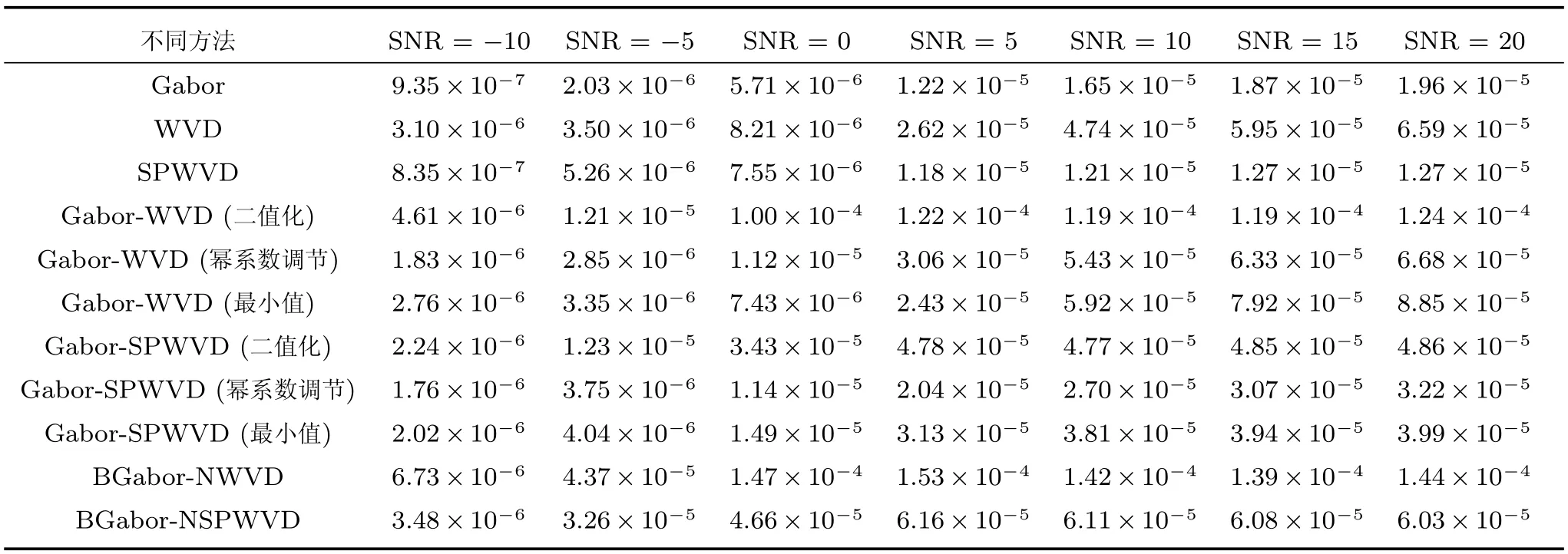
表1 仿真函数f4在不同噪声条件下各方法的聚集度EJP数值比较Table 1 TheEJPnumerical comparison of experimental functionf4in different noise conditions

图9 硬质合金顶锤的现场实物图与三维模拟图Fig.9 Carbide anvil physical site map and 3D simulation figure

在人造金刚石合成加工过程中,硬质合金顶锤在交变的外载应力及热应力作用下,易发生弹性形变和塑性形变.如由于疲劳损坏而产生微观裂纹,这些裂纹不断发展贯穿许多晶粒成为宏观裂纹,使顶锤断面进而发生横向或纵向的破裂或压溃[22].作为高脆性材料,受材料自身特点的正常性破坏和结构、工艺、人为操作等非正常性破坏等因素影响,硬质合金顶锤对于微观裂纹极为敏感,当产生微观裂纹时,由裂纹成核、裂纹扩展延伸并迅速发展成宏观裂纹,产生强烈的声裂发射频率段信号[23].大量实验研究表明,声发射源主要有塑性形变(滑移和孪生)、断裂(裂纹的形成和扩展、第二相质点或夹杂物)、相变(马氏体相变、共晶反映等)、磁效应和表面效应等[22].图9(a)为硬质合金顶锤的工作现场图,图9(b)为硬质合金顶锤的三维模拟效果图.

通过检测硬质合金顶锤工作时的疑似破裂信号,对比正常状态下信号频率特性及裂纹产生时的信号频率特征,判别顶锤破裂的发生与否.目前存在的难点是微小破裂过程中释放的应力能太小,声发射信号相当微弱,在顶锤工作恶劣环境下,受复杂噪声信号干扰,难以有效地设置采集频率窗口和区分破裂频率成分.为有效地接收到破裂信号,需要传感器设置合适的频率检测阈值,可采用时频分析的手段来分析疑似破裂信号,为判断是否破裂提供参考依据.本文利用BGabor-NWVD和BGabor-NSPWVD算法对金属破裂疑似样本信号进行分析,获取其时频联合分布特点,找到疑似金属破裂信号段的时频分布表示.

图10中,图10(a)、10(d)、10(g)为疑似破裂样本信号的时域波形,图10(b)、10(e)、10(h)为采用BGabor-NWVD算法得到的时频分析结果,图10(c)、10(f)、10(i)为采用BGabor-NSPWVD 算法得到的时频分析结果.图10(c)、10(f)、10(i)的时频集中区域较图10(b)、10(e)、10(h)更为明显,在疑似破裂发生时段,3个样本信号的频率分布集中范围,大致分布在100kHz这个较为明显的频率区域.根据BGabor-NSPWVD算法得到的金属破裂频率窗口,将其设置为传感器的破裂判断阈值,用以自动在线监测硬质合金顶锤工作时是否发生疑似破裂,提高了判别几率,取得了较好的效果.

6 结论

针对STFT、Gabor和WVD出现的时频分辨率模糊和存在交叉项等缺点,以及一些结合算法如STFT-WVD和Gabor-WVD出现的三维幅度失真,抗噪性能及鲁棒性能还不理想的问题,本文提出BGabor-NWVD和BGabor-NSPWVD算法.通过对复杂线性调频信号和多分量的正弦频率分量信号进行数值仿真实验,BGabor-NWVD和BGabor-NSPWVD算法在抑制了交叉项的同时,具有较高锐化时频分辨率,两种算法的抗噪性能和鲁棒性也较为理想.由四分量线性调频信号和三分量正弦信号的数值仿真实验可知,BGabor-NWVD的二维时频表示优于BGabor-NSPWVD,BGabor-NSPWVD的三维时频表示优于BGabor-NWVD.BGabor-NWVD和BGabor-NSPWVD算法综合了STFT、Gabor、WVD和SPWVD各自的频率自适应性和良好的时频表示,其时频聚集度评价参数EJP高于其他方法,具有高锐化频率聚集度优点的同时,能够真实还原信号频率分量的幅度.通过硬质合金顶锤工作时产生的疑似破裂样本信号进行时频分析,本文方法可以较为准确地寻找传感器的频率判别窗口,为金属破裂监测设备数据采集卡提供有效的阈值参考.

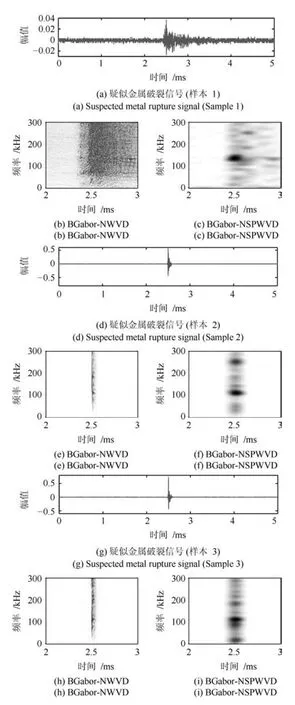
图10 疑似金属破裂样本的时频分析Fig.10 Time-frequency analysis of suspected metal rupture samples