无线传感器网络下基于压缩感知的多目标分层贪婪匹配定位

游康勇 杨立山 郭文彬

随着无线通信技术的进步以及无线传感器网络(Wireless sensor network,WSN)和物联网等的高速发展,如何精确定位监控区域内的多个目标已经成为信号处理领域中极具挑战和实际意义的问题.多目标定位可以应用于诸多场景,例如,WSN中传感器节点定位[1]、室内定位[2]、污染源定位[3]、无线电监控等.

传统的定位算法主要分为两类.一类是基于测距的定位算法,典型算法有利用到达时间测距(Time of arrival,ToA)、利用到达时间差测距(Time difference of arrival,TDoA)、利用到达角度测距(Angle of arrival,AoA)和利用接收信号强度进行三边测距(Received signal strength indicator,RSSI)[4];一类是非测距的定位算法,典型算法有DVhop定位[5]、基于信道感知定位[6]和RSSI指纹定位[7−8]等.然而这些方法都显示出一定的局限性.

近年来,压缩感知(Compressive sensing,CS)理论的兴起[9]为我们提供了一种全新的视角去看待多目标定位问题.通过对感知区域的网格化,目标位置在空间域上的稀疏性为压缩感知理论体系的应用提供了可能.研究表明[10−11],基于压缩感知的多目标定位方法能够实现比传统的定位方法更好的定位性能.Cevher等[12−13]提出了WSN 中多目标定位的估计框架,提出只需少量的测量,便可以将目标位置的稀疏向量通过传感矩阵进行恢复.在此之后,Feng等[10]开始将多目标定位问题建立在压缩感知欠定方程上,并采取了基追踪(Basis pursuit,BP)和基追踪降噪(Basis pursuit denoising,BPDN)等恢复算法进行仿真测试及性能比较.Zhang等[11]使用贪婪匹配追踪(Greedy matching pursuit,GMP)算法替代传统的压缩感知恢复算法,提高了恢复的准确性,同时对传感矩阵是否满足有限等距特性(Restricted isometry property,RIP)[9]进行了证明.Lin等[14]通过融合两种网格下的恢复结果获得了分集增益,提高了定位精度.

然而,之前基于压缩感知定位的研究有诸多不足.1)求解基于压缩感知的多目标定位问题时,基于优化逼近的方法定位精度高但计算复杂,基于贪婪恢复的方法计算简单却定位精度低;2)简单使用一般的压缩感知恢复算法来实现定位,忽略了多目标定位问题中丰富的结构信息,无法有效提升定位性能;3)为降低密集网格划分带来的强相关性,文献中广泛采用的正交预处理方法[10]削弱了原始定位模型中的信噪比,使得定位算法的抗噪性能大幅降低.

鉴于此,本文针对多目标定位问题,给出了明确的系统模型,证明预处理方法削弱模型信噪比,提出一种新颖的基于压缩感知的层级贪婪匹配追踪定位算法(Hierarchical greedy matching pursuit,HGMP).所提算法具有线性计算复杂度,提供了一种利用多目标定位场景中的结构信息实现快速贪婪定位的层级架构,提高了多目标定位系统的定位精度和抗噪声性能.

1 系统模型

本节首先阐述基于德劳内三角剖分的空间网格化方法,介绍基于压缩感知的多目标定位模型及各参数的意义.其次,从压缩感知理论出发,讨论定位问题中目标数、传感器数目、网格数目三者的相互制约关系.接着,证明文献中广泛采用的基于正交的预处理操作本质上降低信噪比.最后,在讨论部分阐述本文的主要动机.

1.1 空间德劳内三角网格划分

不失一般性,设已知存在K个目标的二维感知区域被离散成N个网格点(目标服从感知区域内的连续均匀分布),其中随机均匀散布M个传感器(位置已知),每个传感器测量该点处的接收信号强度(Received signal strength,RSS).在空间网格点数目足够大的前提下,可以用网格点近似估计目标的位置来确定K个目标发射源的位置.

空间网格化是构建定位模型的第一步,文献中广泛采用均匀矩形网格划分.理论上,三角形和四面体是二维和三维空间的单纯形,可以剖分任意复杂的几何形状.因三角剖分具有良好的灵活性和稳定性,20世纪80年代后,对三角剖分的研究飞速发展,除了在有限元分析,流体力学等传统领域大放光彩外,在模式识别,虚拟现实,计算机视觉等领域也得到广泛的应用.

本文采用新提出的基于德劳内三角剖分的空间网格化方法(Delaunay triangulation spatial gridding,DTSG)[14].DTSG方法利用传感器节点和四个边界点作为原始网格点,对感知区域进行初步的德劳内三角剖分,然后依次添加各个德劳内三角形的重心作为新的网格节点,重新对感知区域进行德劳内三角剖分,如此迭代分裂,直至网格点个数满足预设大小.相比均匀矩形网格,其具有灵活、网格多分辨率、网格密度自适应的特点.Lin等[14]的研究显示,统计平均意义下,DTSG网格划分方法的定位性能优于传统的均匀矩形网格划分方法.而实际中,传感器的布置符合一定的先验知识,如在无线电监控中,固定监测站点和移动监测平台往往布置在非法电台出现机率大的区域.所以,这种由传感器节点位置生成网格的空间划分方法更切合实际应用.图1给出了M=50,N=441设定下DTSG网格划分结果.其中黑色圆点为随机布置的传感器节点,灰色圆点为依据DTSG算法生成的网格节点,五角星为目标发射源.图1中的目标发射源节点用于示意定位模型,由DTSG方法可知网格划分与目标无关.

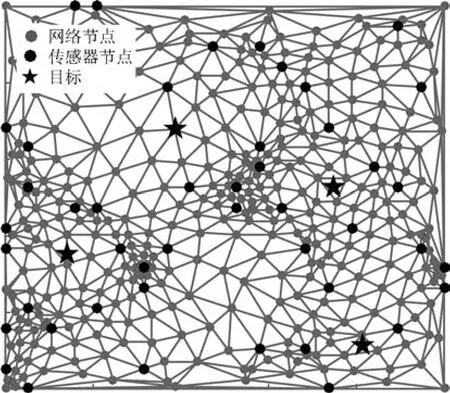
图1 基于DTSG的三角网格划分Fig.1 Triangulation grid using DTSG

1.2 基于压缩感知的多目标定位模型

由于K¿N,所以目标的估计位置在空域上具有稀疏性.根据压缩感知理论,多目标问题可以抽象为通过M维接收信号强度的有噪测量(噪声为测量噪声n,近似为高斯噪声),重建出N维空间中的K稀疏位置矢量的稀疏近似问题.模型为

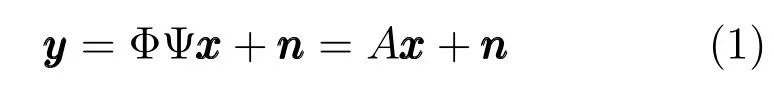
其中,A=ΦΨ称为传感矩阵,是一个过完备字典.在模型(1)中,我们用网格点来近似真实的目标位置.各参数的意义如下:

x=(x1,x2,···,xN)T为K稀疏矢量,编码了目标在网格点中的近似位置.如果目标被近似到第i个网格点上时,xi为与目标功率有关的正数C,否则为0.

2)基于RSS的稀疏基矩阵Ψ∈RN×N

Ψ=[ψ1,ψ2,···,ψN]的每一列ψj代表所有网格点对网格点j处目标的RSS测量.在不考虑信号增益的条件下,网格点j处目标在网格点i上的接收信号强度满足空间传播的衰落模型[10]

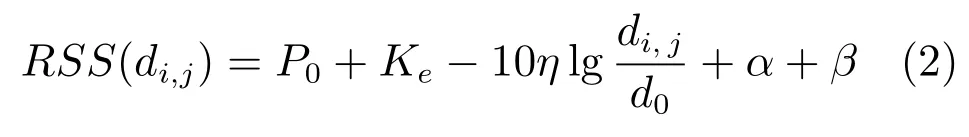
其中,P0为信号发射功率,Ke为环境衰减因子,di,j为网格点j到网格点i的物理距离,d0为近场参考距离.α为快衰落的影响因子,β为阴影衰落的影响因子.显而易见,Ψi,j=RSS(di,j).不同于压缩感知原理中的稀疏基矩阵,例如离散余弦变换基、快速傅里叶变换基、离散小波变换基等,在多目标定位模型(1)中的稀疏基矩阵Ψ很可能不是N维空间的一个基矩阵,即.

3)测量矩阵Φ∈RM×N

测量矩阵表示网格点中的传感器部署方案.多目标定位问题中,稀疏基矩阵Φ的前M列为传

测量结果矢量y为M个传感器的实际RSS测量结果.y=(y1,y2,···,yM)T中的任一元素yi代表第i个传感器感知到的所有目标的功率叠加结果.

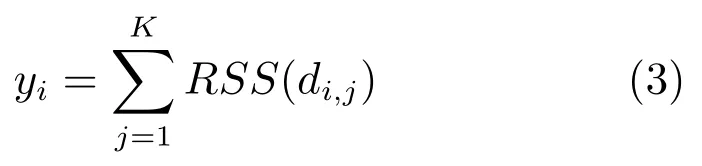
1.3 模型参数的约束关系

在多目标定位问题中,研究者感兴趣的问题是需要多少个接收传感器才能成功定位给定数目的目标发射源?网格划分越密集,是否定位精度会越高?借由压缩感知理论,可以获得关于这些问题的初步结论.

对于无噪声压缩感知方程y=A x,文献[11]证明,若M≥O(Klg(N/K))且A满足(2K,σ)的RIP条件,则范数最小化问题

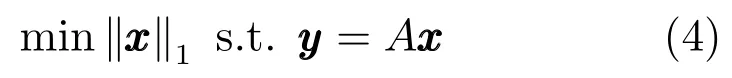
的解为,若x是严格K稀疏信号,则;若x是非严格K稀疏信号,则能重建出x最主要的K个系数.当y受到噪声污染时,压缩感知方程(1)的范数最小化解的重建误差为,其中c0,c1为很小的正常数,为y的重建允许误差范围,为无噪声时的重建误差.

Zhang等[11]证明了多目标定位模型(1)的传感矩阵A以大概率满足RIP条件.所以从压缩感知的重构的角度来看,给定网格划分结果确定了A的构成,而A满足的RIP条件阶数又进一步确定了在当前传感矩阵下能够重构出的最大目标数K.同时,为了重构出稀疏位置矢量x,传感器个数需满足M≥O(Klg(N/K)).

在多目标定位问题中,目标位置的参数空间是连续的.基于压缩感知的定位方法通过把参数空间网格离散化获得对目标位置的网格点近似估计,然后由这些网格点构成有限离散的过完备字典(即传感矩阵A).网格划分越精细,网格点和真实目标之间的误差就越小,但过密的网格会造成稀疏基字典中原子间的相关性越强,进而使得压缩感知的重构性能下降[15],有如下定理[12].

定理1[12].令A∈RM×N为一个过完备字典,为其第j列,定义相干性(Coherence)µ(A)为

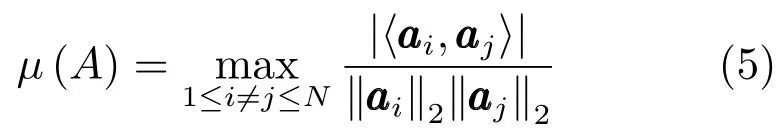
令K≤1+1/16u,当M≥O(Klg(N/K))时,任何K稀疏向量x可以从测量 y=Ax中通过求解式(4)以大概率恢复.

Cevher等[12]的研究表明,在基于压缩感知的多目标定位场景中,µ(A)依赖于∆/2D.其中∆为网格精度,D为网格点和传感器之间的最大距离(由传感器部署和网格划分共同决定).从而,∆决定能够成功定位的目标数的下界,而D决定其上界.

另一方面,为了缓解密集网格划分造成的传感矩阵各列之间的强相关性对压缩感知重建性能的影响,Feng等[10]提出一种基于正交的预处理方法降低了原始传感矩阵各列之间的相关性.此后,这种预处理方法被研究者广泛使用[10,14,16],下面对基于正交的预处理方法做出了详细介绍,并证明在有噪情况下,其本质上放大了噪声的影响,降低了信噪比.

1.4 基于正交的预处理方法及其不足

定义1(预处理算子T).给定模型,定义线性预处理算子为T=QA†.其中,A†表示A的伪逆,Q=orth(AT)T表示对矩阵A的规范正交化操作.

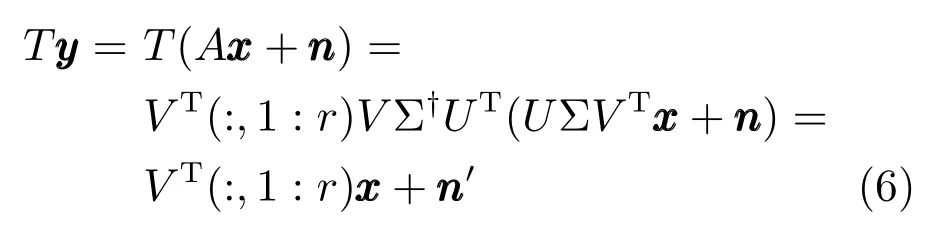
其中,V(:,1:r)为正交矩阵V的前r列构成的子矩阵.可以证明,正交矩阵的随机子矩阵满足RIP条件[17].下文中,称模型(1)为原始模型,模型(7)为预处理模型,相应地,A称为原始传感矩阵,Q称为预处理传感矩阵.

可见,相对原始传感矩阵A,预处理传感矩阵Q的列间相关性已被大大降低.但预处理算子T并不是一个无损操作.从原始模型(1)到预处理模型(7),相对信号功率,预处理算子T放大了噪声水平,即预处理算子T削弱了信噪比(Signal to noise ratio,SNR),有如下定理.

定义2(信噪比SNR).给定模型 y=A x + n,x为随机向量.其中信号为A x,噪声n～ N(0,σ2I).模型信噪比定义为

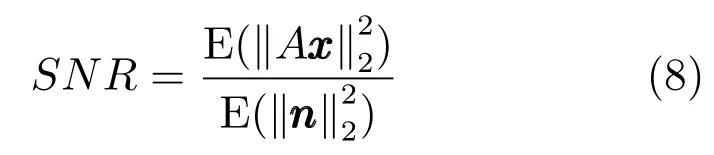
定理 2.给定模型,其中A∈为随机向量且各分量xi满足i.i.d.条件.模型信噪比为SNR1.对应预处理模型为,模型信噪比为SNR2. 如果存在,则SNR2≤SNR1.

证明.A=UΣ1VT.其中,

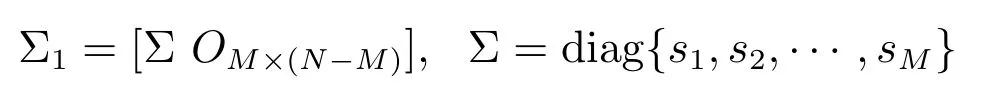
si为A的奇异值.

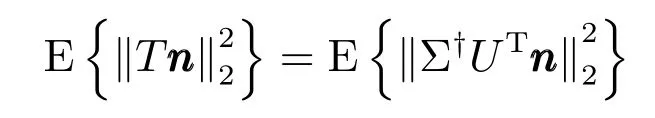
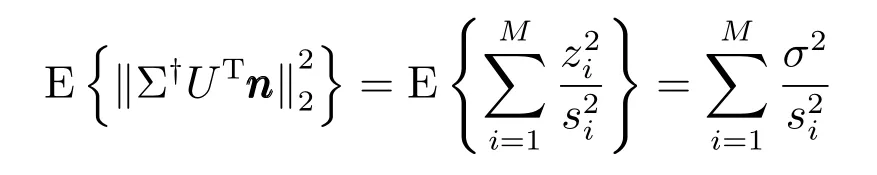
所以

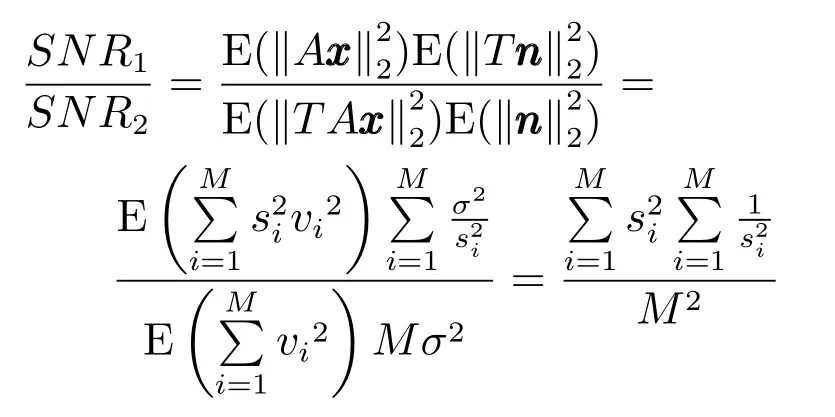
由Cauchy-Schwarz不等式,有

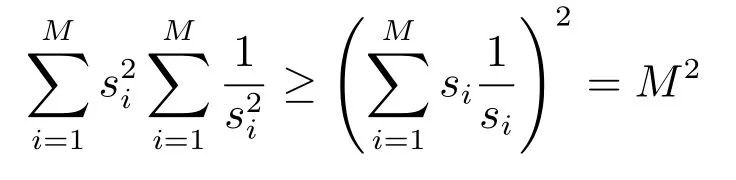
综上所述

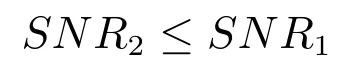
等号成立的条件为:A的所有奇异值都为1.□

在多目标定位模型(1)中,按照空间传播损耗模型构建的原始传感矩阵A,其奇异值一般远小于1,根据定理2,经过预处理算子T处理后,预处理模型(7)的信噪比将远小于原始模型(1)的信噪比.

1.5 讨论

由上述分析可知,密集划分网格会造成A各列间的强相关性,进而影响重建性能.而文献中为降低列间相关性而采取的正交预处理操作又被证明是放大噪声影响,降低模型信噪比.然而,对于定位场景,只有目标附近的字典原子才会对真实的信号构成具有明显贡献,远离目标的位置的原子划分并不会给定位带来益处.所以,对于给定的网格化空间和相应的过完备字典A,可以将观测子空间视为信号子空间和噪声子空间的叠加.

所以,本文的主要动机为以贪婪重建的方式,利用多目标定位场景中隐含的结构信息,从观测子空间中分离出信号子空间,降低测量噪声和网格密集划分所带来的强相关性的影响,提升贪婪恢复的定位准确性.更具体地,原始模型(1)中隐藏着丰富的结构信息,预处理模型(7)适合于贪婪求解,利用原始模型(1)和预处理模型(7)进行联合迭代贪婪定位,将获得更优异的定位表现.

2 层级贪婪匹配追踪定位算法

本节首先分析多目标定位场景中隐含的结构信息.其次,利用这些结构信息提出一种分层贪婪匹配追踪的多目标定位方法(HGMP).最后,对所提算法的收敛性和计算复杂度做出分析.

2.1 多目标定位场景中的结构信息

1)团块模式

原始模型(1)是对多目标定位问题的网格点近似,真实的目标位置可能分布在感知区域的任何位置,不一定精确地在网格点上.所以,接收信号投影到网格空间上的能量将分散在真实目标附近的原子团上.迭代过程中,残差投影到网格空间上的能量将分散在对当前残差贡献最大目标附近的原子团上.具体地,在真实目标位置附近的网格点上,压缩感知恢复系数或残差在网格空间上的投影具有相近的取值,且幅度明显高于远离目标位置的网格点上的,称这种模式为团块模式.图2(a)和2(b)分别展示的是恢复系数在网格点索引集上和网格空间上的团块模式.Yang等[16]注意到了恢复系数的团块模式,其在BP算法的定位结果上利用KNN聚类对恢复位置进行加权平均,鉴于BP算法O(N3)的计算复杂度,其很难被应用到实际中;图2(c)展示的是在原始传感矩阵A上在OMP算法迭代过程中残差的团块模式,可以清晰看到,左边的目标对当前残差贡献最大,其附近的原子团呈现出明显的团块模式;图2(d)展示的是预处理传感矩阵Q上OMP算法迭代过程中残差在网格空间上的投影,由于基于正交的预处理操作打乱了原始传感矩阵A中的相关性,所以不再具有明显的团块模式.本文研究OMP算法迭代过程中残差在原始传感矩阵A的团块模式.

2)冗余信息

如前所述,为了在多目标定位问题中应用贪婪类压缩感知恢复算法,文献中常采用预处理算子T.数学上,T是一个不可逆算子,它把M维非稀疏矢量y映射成r维(r≤M)矢量 z ,再通过z重建N维K稀疏矢量x.前文的分析显示,T放大噪声的影响,降低模型信噪比.此外,预处理传感矩阵Q是一个正交矩阵的子矩阵,相对原始传感矩阵而言,其列之间的相关性已被大大降低.所以相对原始模型(1),预处理模型损失了冗余的信息.对于一个系统来说,冗余虽然带来有效性的降低,但是另一方面,却是系统可靠性的重要保障.在多目标定位问题中,这种冗余信息的损失可以从A和Q的列相关性中得到解释.A中的每一列aj代表所有传感器对网格点j处目标的RSS测量,空域中网格点i和网格点j距离越近,就越相关.所以A的列之间的相关性具有清晰的物理意义.作为这种相关性在残差投影上的反映,投影结果也会在空域上呈现出清晰的相关性,如图2(c)所示,残差在原始传感矩阵A上的投影呈现出清晰的团块模式.与此相反,预处理传感矩阵Q是正交矩阵V的子矩阵,Q的列相关性已经无法直接体现空域上网格点间的相关性.如图2(d)所示,残差在传感矩阵Q上的投影无清晰的团块模式.

2.2 算法步骤

提出的HGMP算法是一种层级的贪婪算法,利用多目标定位场景中的结构信息,具有线性计算复杂度和很好的可解释性.HGMP算法的思想是以贪婪的方式,逐步发掘多目标定位问题中的残差在原始传感矩阵中投影的团块模式,进而利用预处理模型获得贪婪恢复.算法特征为:全局估计层获得目标可能位置的全局估计,稀疏恢复层利用全局估计信息进行目标稀疏位置矢量压缩感知贪婪重建.有以下核心算法步骤.

输入.测量结果矢量y,原始感知矩阵A,目标数K;

图2 多目标定位中的团块模式Fig.2 Cluster pattern in multi-target localization

输出.目标位置恢复点集P,x的K稀疏逼近;

初始化.候选集Ω←φ,残差相关集Λ←φ,删除集∆←φ,残差v←y,格点索引集N←{1,2,···,N};

预处理.计算预处理感知矩阵Q,计算z←Ty;

全局估计层.迭代量i←1,循环执行步骤1～5.

步骤1.寻找对当前残差贡献最大的原子团;

步骤2.利用z和Q,在Λ中进行局部正交匹配追踪,得到Λ上的的恢复系数θ及其支撑集Π;

步骤3.对θ及其支撑集Π正则化,结果为;

步骤4.迭代更新.;

步骤5.如果i≤K,进入下一次迭代,返回步骤1;否则,进入稀疏恢复层,执行步骤6;

稀疏恢复层.

步骤6.扩大候选集

步骤7.利用z和Q,在候选集Ω中进行正交匹配追踪,得到x的K稀疏逼近及其支撑集P;其中,AΩ表示A的索引集为Ω的列构成的子矩阵.步骤1中,Th(v,A)是自适应动态门限,定义为

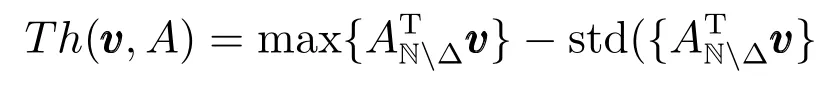
动态门限能够自适应地提取对当前残差贡献最大的原子团,噪声水平高时,残差投影系数的方差较大,动态门限自适应地降低门限值来对抗噪声的干扰,保证空域上与当前残差相关的目标附近格点能够被选入残差相关集Λ.反之,当噪声水平低时,动态门限会提高门限值,减少选入残差相关集Λ中弱相关格点的数目.

步骤3中,正则化[18]处理旨在从恢复系数中找出幅度相近且具有最大能量的子集.给定恢复系数θ及其下标集合Π,在集合Π中寻找子集Π0,满足

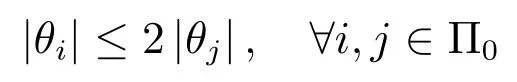
正则化操作选择所有满足要求的子集Π0中具有最大能量的Π0作为输出.

步骤6中,Neighbor(j,D)指在空域上与格点j的欧氏距离小于门限值D的格点集合.

2.3 讨论和分析

1)收敛性和抗噪声性能

不同于一般的基于压缩感知的定位方法,HGMP通过全局估计层获得目标可能位置的候选原子集合,然后稀疏重建层在候选原子集合上获得最终的稀疏贪婪重建结果.这等效于从观测空间中分离出信号子空间,然后在信号子空间上进行贪婪正交匹配追踪.在进行全局估计时,利用原始传感矩阵A上残差投影的团块模式,筛选出对当前残差贡献最大的原子团,然后利用预处理传感矩阵Q易于贪婪恢复的优势获得局部正交匹配追踪恢复结果,最后通过正则化处理从局部恢复结果中挑选出能量最大且贡献类似的原子团.由正则化操作的分析[18]可知,最终全局估计层的输出原子团中一定包含OMP最终估计的K个原子,而稀疏重建层算法是子空间上的OMP算法.所以,在高信噪比条件下,HGMP将和OMP算法保持一致的收敛性.当信噪比较低时,OMP算法易受噪声干扰,陷入局部最优解中,而HGMP挑选原子的方法比OMP更为谨慎,每次挑选出原子团而非单个最相关原子的模式也使得算法对噪声的鲁棒性更强.全局估计层把可能位置从N缩小到候选集Ω,已经极大地去除了噪声造成的虚假目标位置候选点.所以,在此基础上进行贪婪恢复定位具有明显的抗噪声优势.

2)计算复杂度

步骤1中投影操作实质是矩阵向量乘法,门限比对操作实质是一个遍历过程,所以步骤1的复杂度为O(MN).

步骤2把残差的能量正交投影到残差相关集Λ上,实质上是一个OMP子问题,复杂度为,其中C1=card(Λ)且C1¿N.

步骤3中正则化操作实质上是大小为C1的数集上的排序和二重循环遍历过程,复杂度为.

步骤4在候选集Ω中更新残差涉及一个最小二乘问题,复杂度为O(M2C2),其中C2=card(Ω),且满足C2¿N.

步骤6扩大候选集,包含C2个遍历格点集合的操作,复杂度为O(C2N).

稀疏恢复层是候选集上的稀疏度为K的OMP操作,其复杂度为O(KMC2).

综上所述,当N较小时,HGMP算法计算复杂度不高于O(KMN2).当N很大时,HGMP算法的渐进复杂度为O(KMN).

3 算法仿真

为验证所提算法在抗噪性能和计算复杂度方面的提升,采用经典的OMP算法和BP算法作为对比.此外,为了对比算法在DTSG网格划分和均匀矩形网格划分上的性能,对于同样的仿真参数设置,每一次蒙特卡洛仿真中在两种网格上分别进行定位.仿真的硬件环境为Intel Core i7-6700处理器,主频3.4GHz,8GB内存;软件环境为Windows 10+MATLAB R2016a.

3.1 评价度量

平均定位正确率(Mean localization accuracy rate,MLAR).如果在距离真实目标Ti小于1m的范围内能够找到恢复点,认为目标Ti被成功定位,恢复点被称为目标Ti的匹配恢复点.把被成功定位的目标个数#SuccessfulLocalizedTargets与总目标个数#Targets的比值记为恢复的正确率.

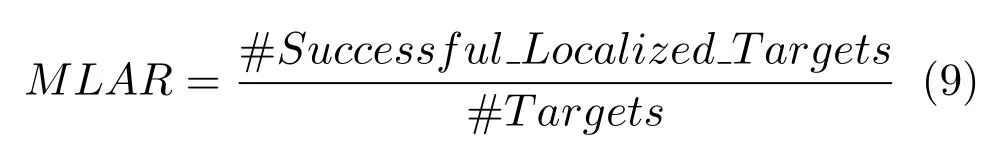
平均定位误差距离(Mean localization error distance,MLED)定义为目标Ti的真实位置(xi,yi)和最近的匹配恢复点位置之间的平均欧氏距离,公式为

平均运行时间(Mean run time,MRT)指每次蒙特卡洛仿真中算法运行时间的平均值,以此来评价算法的时间复杂度.

3.2 仿真参数选择

感知区域设为10m×10m的方形区域,网格点N=21×21,目标数K=4.目标有效全向辐射功率Pt=10dBm.稀疏基字典Ψ采用IEEE802.15.4标准中的室内传播损耗模型[14].

测量噪声为高斯白噪声,为了有效验证算法的定位性能,消除随机因素的影响,取3000次仿真的均值作为实验结果(每一次仿真均重新撒布目标和传感器,重新构造空间网格).

3.3 仿真结果和分析

下文中均匀矩形网格划分简称为矩形网格,DTSG网格划分简称为三角网格.

1)抗噪声性能和计算复杂度

图3和图4分别给出了M=50时,在均匀矩形网格划分和DTSG网格划分下各算法的平均定位正确率和平均定位误差距离受信噪比的影响.可以看出:

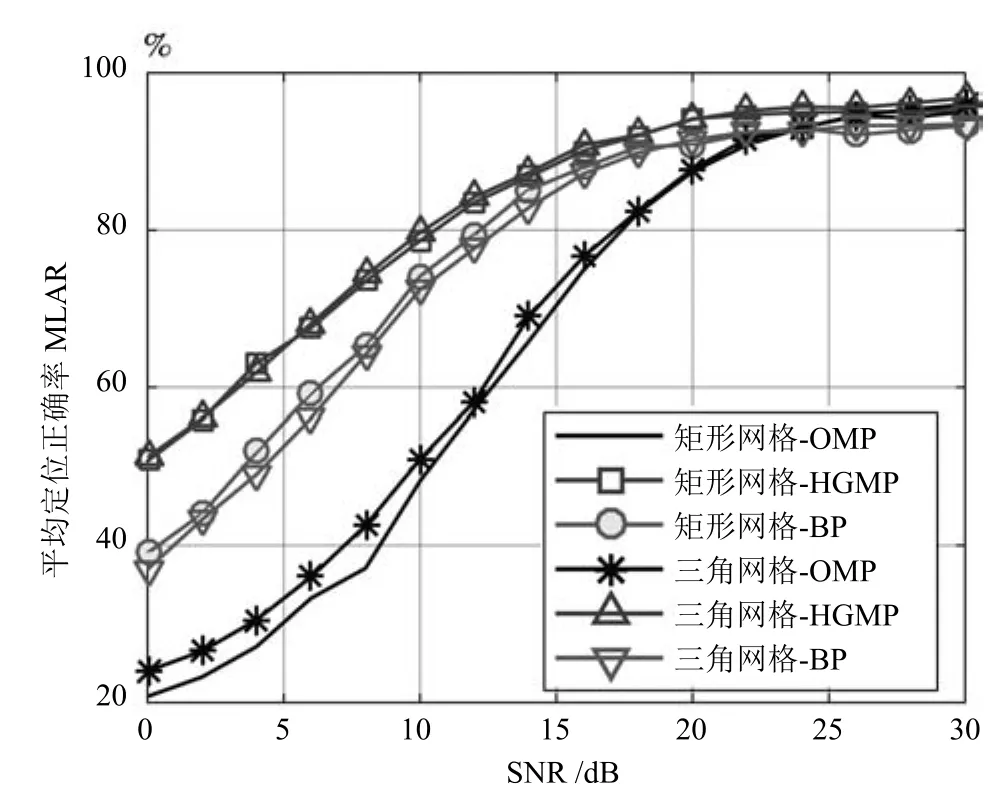
图3 噪声对平均定位正确率的影响Fig.3 The in fluences of the noise level on MLAR

图4 噪声对平均定位误差距离的影响Fig.4 The in fluences of the noise level on MLED

a)随着信噪比的增加,各算法的平均定位正确率不断上升,平均定位误差距离不断下降.当SNR>25dB时,BP和OMP的定位性能趋于收敛,当SNR>22dB时,HGMP的定位性能趋于收敛.由于基于压缩感知的多目标定位模型是对真实目标位置的一个逼近模型,当信噪比大于一定程度时,多目标定位问题中的测量噪声不再是主要矛盾.对于图3,限制MLAR继续增加的主要因素为定义成功定位的精度(仿真中为1m)和网格精度(网格划分带来的模型逼近误差,仿真中平均网格间距为0.5m);对于图4,限制MLED继续降低的主要因素为网格精度.

b)在统计平均意义上,对于BP算法和HGMP算法,DTSG三角网格划分和传统的均匀矩形网格划分的定位性能保持一致;对于OMP,在同样的噪声水平下,三角网格划分能实现比均匀矩形划分更高的定位正确率和更低的定位误差距离.

c)在噪声占主要影响因素的前提下(SNR<25dB),通过在迭代过程中利用残差的团块模式,限制在信号子空间上进行贪婪重建,HGMP的定位正确率和定位误差距离优于BP的,远远优于OMP的,显示出良好的抗噪能力.

图5 不同噪声水平下的平均运行时间Fig.5 MRT under different noise level

图5给出上述实验过程中各算法的平均运行时间.HGMP算法的计算复杂度显著低于BP算法.随着信噪比的提高,HGMP的平均运行时间降低.这是因为噪声水平越低,残差投影的团块结构越明显,投影方差越小,每次选入残差相关集Λ中的格点数目也越少,从而运行时间也越少.同样的噪声水平下,HGMP算法在三角网格划分上的运行时间要高于矩形网格划分的,近似是矩形网格划分的常数倍.这是因为计算残差相关集采取的动态门限函数和残差投影标准差相关,由于三角网格划分的非均匀性和非规则性,其投影方差大于均匀矩形网格划分的,导致三角网格中的残差相关集包含更多的格点,使得三角网格上的运行时间高于矩形网格上的.相对BP算法和HGMP算法,OMP只包含投影、最小二乘、更新残差三个步骤,所以其计算最为简单,但从图3和图4可以看出,OMP低计算复杂度的代价是对噪声敏感,当SNR较低时,定位性能低于HGMP和BP.

2)传感器个数的影响

图6 传感器个数对平均定位正确率的影响Fig.6 The in fluences of sensor numbers on MLAR

图7 传感器个数对平均定位误差距离的影响Fig.7 The in fluences of sensor numbers on MLED

图6和图7分别给出了SNR=25dB条件下,传感器数目为6,8,10,15,30,40,50时,均匀矩形网格划分和DTSG网格划分下各算法的平均定位正确率和平均定位误差距离.可以清晰看出,随着传感器的个数不断增加,各算法的平均定位正确率不断上升,平均定位误差距离不断下降,但变化趋于平缓.对于K=4,M=441,理论上需要传感器的下界为Klg(N/K)≈19.从图6和图7可以看出,当传感器个数小于20时,所有算法的平均定位误差距离都大于1m,平均定位正确率小于70%.当传感器个数大于30时,除了在矩形网格划分上的OMP算法外,其他算法的平均定位误差距离都小于1m,相应的平均定位正确率大于82%.统计意义上,对于1m范围的成功定位精度,经验值和理论值之间的差距为11个传感器.其次,对于同一传感器数目,HGMP在DTSG三角网格划分和均匀矩形网格划分下都显示出优于其他算法的定位性能,且在DTSG三角网格划分下的HGMP定位性能最优.

4 结论

本文给出了一种新颖的基于压缩感知的多目标分层贪婪匹配定位方法(HGMP),并证明了文献中广泛采用的正交预处理操作降低定位信噪比.所提算法从观测子空间中分离出信号子空间,利用原始传感矩阵和预处理传感矩阵进行联合迭代贪婪定位,提供一种利用多目标定位问题中丰富的结构信息实现鲁棒性贪婪定位的层级架构.理论分析和计算仿真表明,HGMP定位算法具有渐进线性复杂度O(KMN).相同信噪比下,HGMP在不同网格划分上均展示出更好的定位性能.