基于维纳滤波和主成分分析的脉冲涡流检测信号降噪方法*

徐志远,伍 权

(1.复杂轨迹加工工艺及装备教育部工程研究中心,湖南 湘潭 411105;2.湘潭大学机械工程学院,湖南 湘潭 411105)

脉冲涡流PEC(Pulsed Eddy Current)检测技术是近几十年来发展起来的电磁无损检测技术,被用于金属导电构件的缺陷检测和厚度、电导率测量[1-4]。其采用脉冲激励信号,相对于采用单频或多频激励的谐波涡流检测技术,检测信号具有更丰富的频率成分[1-2]。同时,脉冲涡流传感器的输出信号主要在时域进行表达,相比于谐波涡流的单一阻抗表达,可供提取的特征量得到极大扩展。这也使得信号处理方法成为脉冲涡流检测的一个重要研究方向,吸引了许多无损检测学者的关注。

脉冲涡流信号时域特征明显:前期为10-1V～102V的过冲信号,量级与激励方波幅值及边沿陡峭度有关;过冲后,信号快速衰减,尾部的后期信号已非常微弱,通常为mV甚至μV级。中后期信号携带了被测构件的深层信息,利用微弱信号处理技术从信号波形中准确的提取出特征量对深层缺陷的检出至关重要。为了从背景噪声中分离出微弱的脉冲涡流信号,信号降噪成为不可缺少的环节,且在此环节中保持信号的原有特征显得尤为重要。Yang等[3]提出了基于匹配跟踪的小波分解方法,用以确定PEC信号的噪声强度,并利用基于噪声强度计算结果的加权平均算法完成特征量数据的估计,抑制了噪声对信号特征量的影响。Huang等[4]提出了一种双对数域中值滤波的信号处理方法,用以抑制铁磁性材料PEC信号的噪声,实验证明该算法比笛卡尔域的中值滤波算法更适合大动态范围信号的噪声抑制。

脉冲涡流信号是典型的非平稳信号。近年来,小波阈值去噪、经验模态分解EMD(Empirical Mode Decomposition)和小波阈值联合去噪方法在处理非平稳信号中得到广泛的应用。但小波阈值去噪中最优阈值的选择一直是研究和应用的难点。EMD和小波阈值结合去噪的方法本质上也存在小波阈值的选择问题,且EMD模态分解时会出现模态混叠现象,使得分解的IMF分量无法表示真实的物理过程[5]。为此,本文根据脉冲涡流检测信号的特征,结合维纳滤波和主成分分析法各自的优势,提出了基于维纳滤波和主成分分析的脉冲涡流信号降噪方法。该方法首先利用维纳滤波从含噪信号中提取有用信号进行信号预处理;再对预处理后的脉冲涡流信号进行差分处理消除部分系统噪声;最后对差分信号进行主成分分析降噪,得到了具有高信噪比的脉冲涡流时域差分信号。

1 维纳自适应滤波和主成分分析

1.1 维纳自适应滤波

脉冲涡流检测通常采用时域波形的峰值、峰值时间、上升时间等特征量进行缺陷的分类与定量识别[6-8]。为准确的提取上述特征量,信号去噪时既要取得较好的效果,又要保证完整的边缘特性。维纳滤波是基于最小均方准则下的最佳线性估计器[9],其利用平稳随机过程的相关特性或者频谱特性对含噪信号进行去噪。假定采集到的脉冲涡流信号为:

x(n)=s(n)+ω(n)

(1)

式中:s(n)为纯净信号,ω(n)为独立的加性噪声。根据滤波准则,估计信号可以表示为:

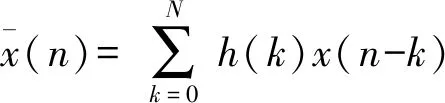
(2)

(3)

式中:Ps(ω)和Pw(ω)分别为检测信号和噪声的功率频谱密度。

实际检测中的PEC信号具有非平稳特性。为增加维纳滤波器对非平稳信号的自适应性,采用加滑动模板窗的方法,将窗内信号视为局部平稳。这时,可在窗内用加权平均的方法计算信号的均值和方差:

(4)

(5)

式中:u,σ2表示滑动窗内的均值和方差;N×M为选定窗的长和宽,窗内信号值为x(i,j),i,j=0,1,…,n-1。

上述滤波过程可表示为:

(6)

式中:y(i,j)为滤波后输出的信号,v2表示输入信号长度内噪声的均方差值。根据窗内局部信号的方差σ2即可调整信号输入和输出的关系,达到自适应的效果。可以看出,当σ2较大时,滤波器的滤波效果不明显,当σ2较小时,滤波效果较好。这种通过窗内局部方差来自动调整信号滤波效果的方式,比线性滤波器具有更好的选择性。

1.2 主成分分析

PCA方法利用降维或者去除矩阵中的重复信息进行信号消噪。降维时将原样本X投影到一个新的空间Y中,这一过程相当于与某一矩阵A相乘,可表示为:

(7)

式中:y1,y2,…,yq为原变量X的第1,2,…,q主成分(q≤n)。记为:

Y=AX

(8)

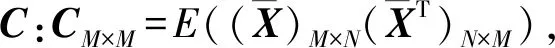
将式(8)两边左乘AT,可得ATY=ATAX,由于系数矩阵A为正交阵,则ATA=1。原矩阵重构表示为:

X=ATY

(9)

将上式代入式(9)中,可得到信号重构矩阵。阈值p以后的各主成分包含了大部分噪声,重构时将系数置0,就可以有效的去除噪声。

对PEC信号直接应用维纳滤波会得到较高的信噪比,且能保证较好的边缘特性。但是,实际滤波表明,在弱信噪比的情况下维纳滤波后信号仍含有很多噪声,且信号中局部方差变化太大的部分滤波效果不明显。针对这一现象,选用主成分分析法对维纳滤波后的信号进行后续处理,提取信号的主成分特征,去除信号的细节噪声分量及一些突变点,进一步提高信噪比。

1.3 基于维纳滤波和主成分分析的脉冲涡流检测信号降噪方法

基于以上分析,提出基于维纳滤波和主成分分析的脉冲涡流检测信号降噪方法,其具体实施步骤如下:①分别对采集到的被测试件不同位置处原始信号进行维纳自适应滤波,从强背景噪声中提取出微弱的有用信号,得到较高信噪比的检测信号;②选取无缺陷处(或名义壁厚处)的检测信号为参考信号,与其他位置处检测信号进行差分处理;③将差分后的信号作为研究对象,分别构造Hankel矩阵;④对每个Hankel矩阵进行主成分提取,通过计算主成分的贡献率确定重构主成分个数;⑤根据步骤④中确定的主成分个数,去除噪声分量,重构信号,得重构后的时域差分信号;⑥提取具有高信噪比的时域差分信号的特征量,比照标定曲线,对试件进行缺陷定量或壁厚测量。

2 降噪效果评价指标

在PEC检测系统运行时,不加激励信号执行信号采集操作,此时采集到的信号为纯噪声信号,且为噪声的最低水平。噪声水平可以通过下式进行计算[4]:

(10)

以上式计算出的最低噪声水平作为参考值,得出信号在衰减过程中首次达到最低噪声水平所需的时间μ。通常在μ以后仍含有有用信号淹没在噪声中,为得到更为纯净的噪声信号,选取3μ～5μ后的信号作为噪声信号,并通过下式进行噪声能量计算:

(11)

式中:sn[k]为噪声信号;L为对应信号的长度。

分别计算信号处理前后对应段噪声能量Pn1和Pn2,按式(12)计算出信噪比提高值,作为降噪效果评价指标。

SNRimprove=10lg(Pn2/Pn1)

(12)

3 实验和结果分析

3.1 实验系统

为验证上述去噪方法的有效性,以图1所示宽度为100 mm,厚度分别为5、15、18和20 mm的Q235阶梯板为试件搭建脉冲涡流检测实验系统[15]。该系统由信号发生模块、功率放大器、脉冲涡流探头、前置放大器、数据采集卡和上位机六部分组成,其照片图如2所示。

图1 阶梯板试件

图2 实验系统

内径/mm外径/mm高度/mm线径/mm匝数激励线圈20.860.642.01.0840接收线圈75.679.74.40.1800

3.2 实验和数据采集

运行该系统,设定信号发生模块参数,在其中施加频率1 Hz、电压1.2 V的激励信号,通过功率放大电路作用于探头激励线圈,在阶梯板试件中激发出脉冲涡流。接收线圈将阶梯板中的涡流场感应成电压信号,经前置放大电路进行放大,再接入信号采集系统,系统以20 kHz采样频率进行数据采集,并将数据实时存储在嵌入式计算机中以便后续降噪处理。

探头参数见表1,激励、接收线圈同轴放置。实验中通过移动探头,获取它对不同阶梯板厚度的检测信号。图3(a)是在实验中采集到的信号时域波形。由于信号在采集过程中经过前置放大电路,前置放大电路有限的供电电压导致前期部分过冲信号的幅值饱和而出现“削峰”现象。

3.3 维纳滤波及模板窗的选择

维纳自适应滤波根据局部均值和方差来实现滤波效果的自动调节。在进行自动调节的过程中噪声均值和方差估计需要选择模板窗。模板窗的选择不是一成不变的,模板窗太小,均值和方差受噪声影响较大,信号去噪效果不佳;模板窗太大,则失去自适应性,平稳性也难以得到保证。为选取适应PEC信号滤波的模板窗,选取2×2,3×3,5×5,7×7,9×9等5个模板窗进行滤波效果比较,得到如图3(b)～3(f)所示的滤波后波形。

从图3可以看出,选择不同阶数的矩形窗滤波后,信号含噪声幅值明显低于图3(a)原始信号噪声幅值,但不同模板大小去噪效果存在差别。图3(b)中2阶模板窗滤波后虽仍然含有较大噪声,但中后期信号失真较小,失真度明显低于其他各阶窗滤波后信号。应用上一节的降噪效果评估方法,计算出噪声的最低水平值为2.3 mV,信号首次衰减到噪声水平的时间μ为0.001 3 s。选择4μ后的信号进行噪声分析,并计算去噪后信号相对原始信号的均方根误差RMSE,来衡量去噪后信号的失真程度。滤波前后信号的SNR改善值和RMSE值如表2。

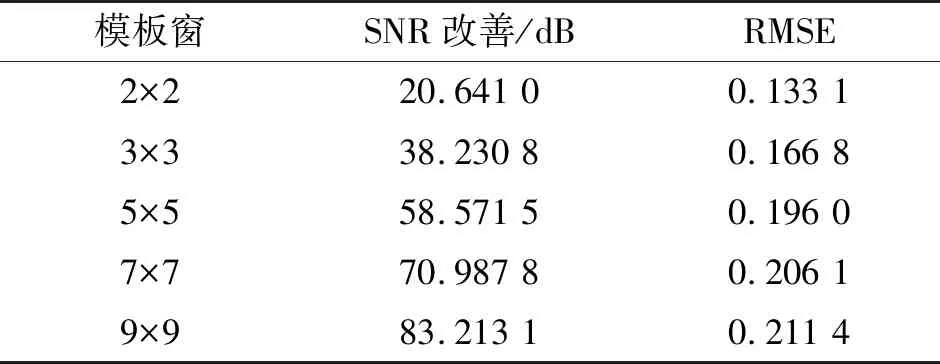
表2 选择不同模板窗进行维纳滤波后信号对比

从表2中可以看出,随着选取模板窗的增大,信噪比改善效果越好,但与原始信号的偏差变大。对照图3可见,随着滤波阶数变大,中期信号曲线(0.005 s～0.01 s区间)出现的失真也随之变大。为使滤波后信号保留完整的边缘信息和细节信息,选用2×2的模板窗进行脉冲涡流检测信号维纳滤波预处理。这样,滤波后信号既能改善信号信噪比,也能保持良好的边缘特性。具体信噪比改善值如表3。

表3 维纳滤波后信噪比改善关系

图3 用不同模板窗进行信号去噪效果比较

图4 维纳滤波和PCA重构信号差分图

3.4 预处理信号主成分分析

脉冲涡流检测进行信号采集时,系统和实验环境都会带入相应的噪声。通常采用差分的方法进行信号特征的提取[16]。以厚度最大区域(20 mm)作为参考区域,用参考区域的检测信号分别与其他阶梯检测信号相减得到脉冲涡流差分信号,如图4所示。图4(a)为原始信号直接差分后的信号图,可以看出信号完全淹没在噪声中,很难从中直接提取出区分阶梯板厚度的特征量;图4(b)为维纳滤波后差分信号,虽然也不能直接提取出特征量,但在很大程度上提高到了差分信号的信噪比。

运用PCA进行信号处理时需要满足被提取的信号在混合信号中占主要成分,如果大幅度的噪声信号出现过多,就会被当成主成分进入信号空间,从而产生重构误差。维纳滤波为后续PCA降噪奠定了基础。

用维纳滤波预处理后的差分信号分别构造原始信号矩阵。矩阵构造的方法通常有两种:①连续截取m段长度为n的信号构成m行n列矩阵;②重构吸引子矩阵法。选择重构吸引子矩阵法,令t=1,τ=1,进行Hankel矩阵的构造。矩阵的秩越大,分解阶数越大,可以使噪声信号的能量相对分散,从而凸显出特征信号,有利于特征信息的提取。因此,矩阵的行列个数越接近,信号的去噪效果越好[13-14]。取差分信号中前1 600个数据点构造801×800 Hankel矩阵,进行PCA处理,得到信号的主成分。

信号去噪效果的好坏取决于重构阈值的选择。PCA重构法通常依据贡献率确定阈值p。为确定信号重构的p值,利用式(7)将5 mm阶梯处的PEC差分信号分解成800个主成分。图5为差分信号前6个主成分根据式(9)分别重构图。从图中可以看出,信号主要集中在前4个主成分中。从第5个主成分开始信号中开始伴随有大量噪声,第6主成分完全被噪声淹没。因此,可视第5主成分为信号和噪声的分界阈。经计算可得到前4个主成分的累积贡献率达81.52%。选取前4个主成分进行重构,得到5 mm阶梯处PEC差分信号的重构效果如图6所示。

图5 PEC差分信号的单个PCA主成分分量重构图

图6 前4个PCA主成分重构的PEC差分信号

图7 维纳滤波和PCA处理后PEC差分信号

重复上述PCA分解、重构过程,将15 mm、18 mm阶梯处的差分信号执行上述操作,得到所有阶梯区域降噪后的差分信号,一并绘于图7。与图4(b)相比,可见经过PCA处理后,PEC差分信号信噪比得到进一步提高,不同厚度区域的信号波形能明显区分。

此时,信号特征量与试件板厚的定量关系得到凸显:随着阶梯板厚度的增加,差分信号的幅值减小。经维纳滤波和PCA后差分信号的信噪比得到大幅提高,具体数值对比如表4所示。

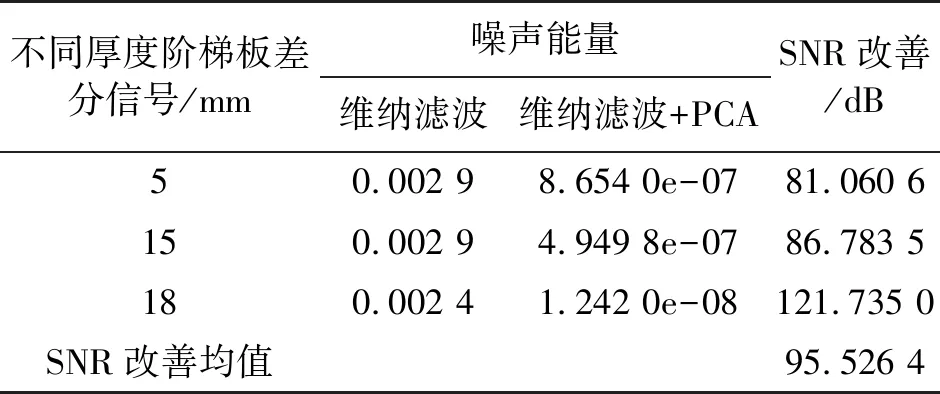
表4 经维纳滤波和PCA处理后PEC差分信号信噪比改善比较

4 结论

为准确提取强背景噪声下微弱的脉冲涡流检测信号的特征量,本文提出了一种基于维纳滤波和主成分分析的脉冲涡流信号降噪方法。该方法首先采用维纳自适应滤波进行信号预处理,消除信号中强噪声污染;再应用主成分分析对维纳滤波后的差分脉冲涡流信号进行主成分提取,进一步提高了信噪比。

该方法充分利用了维纳滤波和主成分分析对信号降噪的各自优点。针对噪声强而有用信号微弱的原始信号,通过选择合适的模板窗进行维纳滤波,在提高信号信噪比的同时保证其失真小。进一步地,为避免对仍具有较大噪声的信号直接进行主成分提取,将维纳滤波后的信号先进行差分,再进行主成分分析,减小了噪声被当成主成分的可能性,从而保证了主成分提取的准确性。运用该方法对阶梯钢板脉冲涡流测厚信号的处理结果表明,信号的信噪比得到大幅提升,信号特征量随壁厚变化的规律得以凸显。