静水中悬臂同轴圆柱壳的流固耦合振动分析

张德春，鲁 丽，李 鹏，杨翊仁

(西南交通大学 力学与工程学院，四川 成都 610031)

0 引 言

目前，同轴圆柱壳在反应堆结构中得到广泛的应用，而其在水中的振动频率是结构设计中重要的指标，科研人员对此做了大量研究[1-9].例如，Krajcinov-

ic[5]计算了无限长同轴圆柱壳在水中的振动频率，并分析了间隙对频率的影响；骆东平[6]研究了任意边界圆柱壳振动问题，得到了圆柱壳频率和振型的精确表达式；Naumann[7]假设圆柱壳径向振型为梁振型，计算并讨论了无加筋和加筋圆柱壳的振动频率；Kwak[8]对部分浸在无限大域和环形域流体中的悬臂圆柱壳频率进行了分析.综合分析可知，目前解决圆柱壳振动的思路有两种：其一是从壳体的运动方程出发，通过时频域变换或模态展开及伽辽金离散来求解壳体的振动频率，该方法比较直观，但计算过程比较复杂；其二是先计算结构的能量，再通过变分的方法对壳体的振动进行分析，该方法计算过程简单，但在考虑流体黏性作用时该方法不易列出能量方程，故只适用于无黏流体.在些基础上，本研究考虑内外壳的相互作用，通过能量方法对浸入在理想流体中的悬臂同轴圆柱壳的振动频率进行了分析和讨论.

1 力学模型及计算方法

作为研究对象的同轴圆柱壳结构如图1所示，其结构一端固定一端自由，且完全浸没在静止流体中.其内壳的密度、弹性模量、泊松比、厚度、中面半径分别为ρ1、E1、ν1、h1；外壳的弹性模量、泊松比、厚度、中面半径分别为ρ2、E2、ν2、h2；内外壳的长度均为L.流体考虑为无黏不可压缩的理想流体，其密度为ρF.

图1液体中同轴圆柱壳示意图

对圆柱壳体，假设其径向、周向、轴向的位移分别为u，v，w，则圆柱壳体的动能和势能分别为，

(1)

(2)

对于所研究的壳体，若h≪R，则认为该壳体为薄壳.对于薄壳，可忽略壳体的横向剪切变形、横向挤压变形和横向挤压应力，由此可推导出Flügge壳体本构关系[10].

基于该本构关系方程可得出壳体势能为，

(3)

应用文献[4]的模态展开法，进一步假设，

(4)

式中，Xm(x)为第m阶梁振型.对于悬臂梁，有，

Xm(x)=(cos(βmx)-ch(βmx))+

(5)

式中，βm为cos(βl)ch(βl)=-1的第m个解.

将式(4)分别代入到式(2)和式(3)中可得，

(6)

式中，x1=[ABC]T，

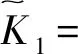
参数E、F、G、H为与振型有关的常值，分别为，

对于外壳，同样假设其振型为，

(7)

代入到式(2)和式(3)中得到，

(8)

需要注意的是，由于结构的对称性，n=n′，且Φ只能取0和π，其分别意味着同相和反相.

2 流体附加质量

对于本研究考虑的理想流体，设其势函数为，φ=y(x)f(r)cos(nθ)eiωt，其满足拉普拉斯方程，

(9)

变换上式，得，

(10)

同时，考虑端部的边界条件，

(11)

(12)

式中，c(t)由内外壳体的端部运动条件确定，设，

(13)

经推导，方程(10)的解为，

(14)

壳体上的边界条件是，

(15)

由式(4)、(15)，可得到，

y(x)=Xm(x)

(16)

对于区域II的流体，其势函数只与内壳运动有关.根据式(16)可得到，

(17)

对于区域I的流体，其势函数可写为，

φI=φIi+φIe

(18)

式中，φIi表示内壳振动外壳不动引起的流体势，φIe表示外壳振动内壳不动引起的流体势，由式(16)，其二者分别为，

(19)

(20)

获取流体速度势后，计算得到流体动能为，

(21)

其α、β、γ由数值计算得到.

由式(6)、式(8)和式(21)，计算得到系统动能和势能分别为，

式中，

对能量取变分，有δ(T-V)=0，即，

(22)

为使式(22)有非零解，必然有，

(23)

根据式(23)可求出耦合结构的频率.

3 间隙对频率的影响

由式(23)可以看出，结构频率受外壳密度、弹性模量、厚度、半径和长度以及流体的密度和间隙影响.本研究重点关注间隙对频率的影响，暂不考虑其他因素的影响.

1)考虑内外壳材料相同的情况，ρ=7 850 kg/m3，E=2e11 Pa,h1=h2=0.01 m,R1=1 m,R2=1.2 m,L=5 m.流体为水，ρF=1 000 kg/m3.

此情况下，计算的前五阶振动频率与ANSYS的计算结果的对比如表1所示.图2给出了第一阶模态计算结果.

图2一阶模态图

从图2可以看出，对于第一阶模态，内外壳环向的峰值均有2个，即n=2，而轴向无拐点，即m=1.另外，从图2还可以看出，内外壳的最大值位置并不相同，此意味着反相.依据此思路对前五阶模态进行分析即得到表1.

表1 频率对比表

由表1可知，本方法得到的解与数值解吻合较好，表明了本方法的准确性.

2)为分析间隙对频率的影响，视间隙值为连续变量，计算其较低阶频率随间隙变化情况如图3所示.

图3振动频率随间隙变化图

由图3可以看出，悬臂同轴圆柱壳结构的振动频率随着间隙的减小而减小，而且减小得越来越剧烈.当间隙接近0时，结构的频率也趋于0，这是因为对于理想流体，当间隙为0时附加质量无穷大[13]的缘故.事实上，当间隙很小时，理想流体的假设不再成立.

4 结 论

本研究提出了一种基于能量法求解悬臂同轴圆柱壳结构频率的普适方法，并分析了间隙对水中同轴圆柱壳结构频率的影响.本方法也可以用于计算内外壳支撑形式不同的情况，当内外壳长度不同时，选取适当的势函数，可以计算出结构的频率.