借助几何直观，助推意义理解——“画长方形解决问题”教学思考和实践

□ 邵珠利

通过画长方形解决问题的学习为学生打开解决问题策略的一扇窗。于是笔者想到在四年级上学期教学了单价×数量=总价、速度×时间=路程这两个数量关系式后，设计“画长方形解决问题”，将不具有“长方形元素①长方形元素指的是题目中出现了“长方形”字样，如长方形花坛、长方形草坪等，这些具有“长方形元素”的信息会有暗示作用。不具有“长方形元素”，指的是没有这些暗示信息。”的实际问题中的数量关系与长方形面积建立关联，进而通过画长方形，借助几何直观，助推意义理解，帮助学生有效分析、解决问题。

一、课例回放：围绕主题情境，自主构建生成

（一）课前互动，营造氛围

介绍××小学及区艺术节举行的情况。

【设计意图】区艺术节是本节课的主情境，本节课主要围绕在区艺术节中遇到的实际问题而展开研究。教师介绍既能让学生快速了解××学校，又为本课学习渲染了氛围。

（二）对比关联，初步感知

1.画图分析，列式解答

2.对比分析，感知模型

（1）四图对比，建立关联

师：这几位学生虽然画的图形不一样，但算式都相同，都是75÷5=15（排），20×15=300（人）。

师：在这几幅图中，你更喜欢哪一幅，为什么？小组内交流想法。

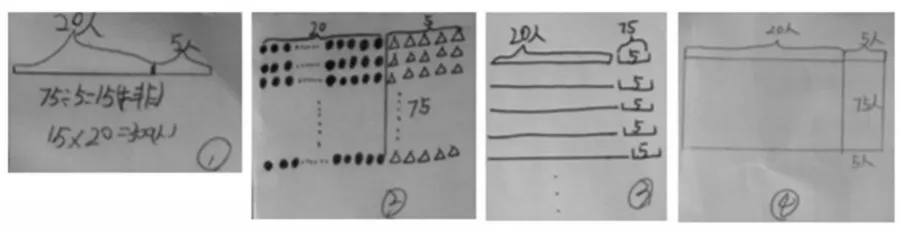
生：我们组喜欢第④幅图。因为它比较简洁、比较清楚。

生：我们组也喜欢第④幅图。大家看，虽然第①幅图比较简洁，但是不能完整表示所有信息；第②幅图虽然比较具体，但太麻烦了；第③幅图虽然比前两幅图清楚，但还是有点麻烦；只有第④幅图比较具体，能表示出所有信息，而且比较简洁。所以我们组也喜欢第④幅图。

师：这四幅图之间有什么联系呢？

生：第①幅图表示的就是第②③④幅图中一排的情况。

生：第②幅图和第③幅图的想法其实是一样的，都是先表示出每排的人数，再表示排数，因为不知道具体的排数，所以两位同学都加上了省略号。最后都在刚才的基础上表示出每排增加5人，就增加75人。

生：第②幅图、第③幅图简化后就是第④幅图。每排的人数就是长方形的长；排数就是长方形的宽；总人数就是长方形的面积。

师：你们这个发现太棒了，我要把它画出来并记录下来。（师在黑板上画长方形,并进一步规范画法，明确要在图中既表示出“已知信息”，还要表示出“所求问题”）

（2）拓展联想，感知模型

师：我们知道长方形的面积是长与宽的积。通过刚才的分析，我们发现，长方形的面积还可以表示谁与谁的积？

生：每排人数与排数的积。

师：想一想，长方形的面积还可以表示谁与谁的积？

生：长方形的面积还可以表示数量与单价的积。

师：你的意思就是长表示单价、宽表示数量，面积就表示总价。

生：长方形的面积还可以表示速度、时间的积。

师：你的意思就是长表示速度、宽表示时间，面积就表示路程……

师：观察这些数量关系，你有什么发现？

生：它们都表示两个数的积。

师：是的，一般情况下，当表示两个量之积的数量关系时，画长方形更直观，更便于帮助我们分析解答问题。但在画长方形时，我们一定要明确长表示什么、宽表示什么。（随着学生的回答，适时生成板书内容，见右图）

【设计意图】学生对画图并不陌生，并且也比较习惯画实物图、示意图或线段图来分析解决问题。此题信息中没有“长方形元素”，自然不存在要求学生画长方形的暗示；另外笔者之所以没有强调要画长方形，目的就是要充分暴露学生的原有认知。通过对四幅图的对比分析，学生充分感知了长方形图的特点及画法，并初步感受到当表示两量之积的数量关系时画长方形更直观、形象。画长方形帮助分析解决问题水到渠成。但画图的时候一定要明确长表示什么、宽表示什么、面积表示什么。

（三）例1变式，对比画法

师：同学们，刚才我们不知道排数，解决了这个问题。现在每排的人数也不知道，但是知道信息：如果增加3排，就要增加60人。其他条件不变，你还会解答这个问题吗？

师：这两位同学画的图形不一样，能看懂这两幅图表示的意思吗？

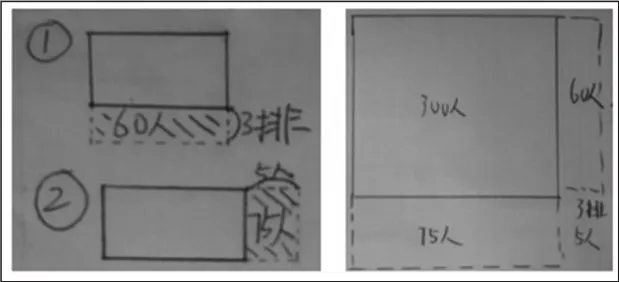
生：第一个同学分开画两幅图，分析起来比较方便；第二位同学合在一起只画一幅图，更加简洁。

师：我们可以像第一位同学这样分开画两幅图，也可以合起来只画一幅图，都能很好地帮助我们分析问题。

师：观察图形，解答这个问题的关键是什么？如何列式？

生：关键就是要求出每排的人数和排数，即求出长方形的长和宽。根据学生的回答课件动态逐条呈现下图内容。

【设计意图】例1是一个量变化，画长方形图进行分析；而例2是在例1的基础上，两个量都变化，画长方形图进行分析。当两个量都变化时，可以只画一幅图，比较简洁；也可以画两幅图，分析起来比较清楚。但不论如何，关键就是要明确长表示什么，宽表示什么，面积表示什么。

（四）课堂小结，明确关键

师：通过这节课的学习，你有什么新的收获？（根据学生概括适时生成板书）

师：你认为画长方形解决问题的关键是什么？

生：关键是明确长、宽、面积所代表的量。

【设计意图】通过对例1和例2的回顾梳理，进一步明确画长方形解决问题的关键，掌握画长方形图的方法与技巧。

（五）图形变式，综合运用

师：接下来艺术节要进行合唱比赛，老师计划给合唱队的学生购买一批上衣。集团校长去询问情况，两位老师是这样说的：

我去询问情况，两位老师又是这样说的：

你们能帮校长和我解答这两个问题吗？

学生独立解答完成后，反馈交流重点如下：

第1题强调长表示什么、宽表示什么、“降价”怎么画。

第2题强调对比分析（见下图）：将画成“一增一减”（图形符合题目要求）与“两增”（图形不符合题目要求）的图形进行对比分析，为什么图形不同，但得数相同？

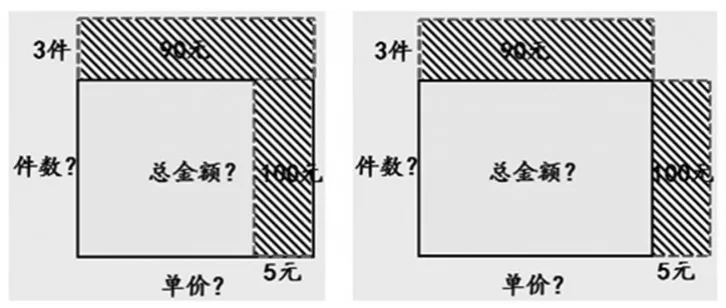
【设计意图】试一试1和试一试2的情境与例1和例2情境不同，研究的是单价、数量与总价的数量关系。另外，画图方法也不相同，试一试1是“一减”的情况、试一试2是“一增一减”的情况。

通过试一试1的练习，学生明确增加的时候向外画，而减少的时候要向内画。通过试一试2正确与错误的两幅图的对比分析，学生进一步明确在画图的时候要根据题目信息画出正确的图形。此题通过两幅图的分析所得到的算式都是正确的，其原因在于“每件降价5元，就能节省100元”和“每件涨价5元，就要多付100元”，虽然画法不同，但是100÷5=20（元），表示的都是这件衣服的单价，所以即使图形画错了，但结果还是正确的。

通过变换情境及画图方式，教师进一步培养学生据题画图并依图析题的意识与能力。

（六）沟通模型，积累经验

师：（同屏呈现）我们今天研究了一增、两增、一减、一增一减四种情况，但不论是哪种情况我们都必须事先明确长表示什么，宽表示什么，面积表示什么。

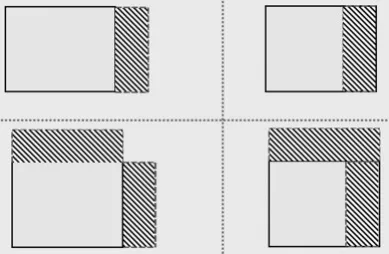
【设计意图】随着讲解与回顾，逐个呈现今天所研究的每种情况，最后同屏呈现这四种情况。通过同屏对比，对今天所研究的四种模型进行整体感知，同时寻求共性，即画长方形解决问题的关键就是要明确长表示什么，宽表示什么，面积表示什么。（最后一张PPT呈现这个内容）同时使学生进一步感知对于研究两量之积关系的题目画长方形解决问题更直观、形象，便于分析解决。

二、课例反思：借助几何直观，助推意义理解

（一）创设优质情境，激活原有认知

在试教时，所创设的情境具有“长方形元素”，所以学生自然能想到用画长方形图进行分析，看似非常圆满，但实际学生是在画长方形解决长方形本身的问题，意义不大。思前想后，到底什么情境更有利于学生自主建构画长方形解决问题的认知？笔者想到了队列问题，这是学生非常熟悉的情境。队列问题本身存在长方形的影子，但它又不同于长方形花坛、长方形鱼池等情境，笔者称其为不具有“长方形元素”的情境，这对学生来说具有挑战性。学生最初画的线段图、圆圈图、简化圆圈图等都是学生对于解答队列问题积累的原有学习经验的有效提取，通过对不同图形的对比分析，不断明晰画长方形解决问题的优越性，由此，用画长方形解决两量之积数量关系的问题也就达成了共识。

（二）巧设关联问题，保持探究兴趣

学生是否能够进行自主学习、自主学习投入程度如何主要取决于教师设计的问题优质与否。本课中围绕艺术节参加队列表演的人数、合唱队购买服装等实际问题展开探究，从例1变式到例2，从画“一边增加”“两边增加”的长方形图到画“一边减少”“一边增加、一边减少”的长方形图，学生始终保持较高的探究热情。问题情境看似不变，但问题本身又着实发生了变化；图形看似相同，但的确又不相同，但不相同之中又有相同之处。一切都给学生以魔力，探究其中，其乐无穷。

（三）加强对比分析，感悟画图关键

“画长方形解决问题”从“一增”“两增”到“一减”“一增一减”，图式在不断发生变化。在解决这些问题时，学生不但要掌握长方形图的画法，更应明确画长方形解决问题的关键就是要先确定长表示什么，宽表示什么，面积表示什么。因此笔者创设多次对比分析的学习活动，增强学生对这一关键问题的感悟，不断积累学习活动经验。

一是播前稻种用杀菌药剂进行浸(拌)种处理，预防恶苗病、干尖线虫病等种传病害。二是使用35%丁硫克百威干粉种衣剂拌种，对水稻苗期稻蓟马持效期达30天以上。通过稻种药剂处理，既能有效控制病虫发生，又显著减少农药的用量。

（四）渗透几何直观，积累活动经验

毫无疑问，画长方形是解决问题的一种有效策略。在解决平均数问题、分数乘法问题，尤其是解决一些稍复杂的两量之积数量关系的问题时，画长方形图往往会使问题变得简单易懂。

对于解决两积数量关系的问题，画长方形图更加直观、形象，有助于分析数量关系，促进学生对题意的有效理解，这彰显了数形结合的魅力。形使数更直观，解题更加有效，课堂更加精彩，在不断画图分析的过程中，经验积累也更加到位。

三、课例延展：着眼课程开发，有效实施教学

本课例作为一次解决问题策略教学的大胆尝试虽然总体比较成功，但从课堂教学实际情况来看，学生对于长方形面积的深入理解，以及据题画图、依图析题等方面仍有进一步探究的空间，下面也谈一点不成熟的思考。

（一）对于“长×宽=面积”的理解不能仅停留在公式层面

如下图所示，教材编排的内容是通过拼摆操作，发现规律，探索得出长方形面积的计算方法。但教材中所涉及的练习只是情境不同，其实都是已知长、宽比较简单的计算长方形面积的内容，属于对公式的直接运用层面。

1.推导长方形的面积要重点关注理解“几个几”

在学生拼摆推导的时候，要重点引导学生理解“每行摆5个，摆了3行”，即3个5；或者“每列3个，摆了5列”，即5个3。只有学生头脑中建立了长方形的面积就是“几个几”的认知，学生才容易理解：如果长表示单价30元，宽就可以表示数量5件，即5个30元，面积就是总价150元；或者长表示每排20人，宽就可以表示有15排，即15个20，面积就是总人数300人。只有这样，学生才能真正将数量关系与长方形面积建立关联，理解才能更加到位。

2.要拓展对于两数求积算式意义理解的认知

学生在三下年级学习了“长方形面积”之后，教师可以有意设计“看式说事”练习。以25×12为例说明操作方法。

（2）如果沿着长摆边长为“1”的小正方形，可以摆多少个？可以摆几排？（重点促进学生对“几个几”的理解）

（3）25×12这个算式，可能还讲了一件什么事？

生：每排25位学生，12排一共有多少位学生？

生：每个书包25元，买12个书包要多少钱？

……

（4）教师课件演示用小正方形换学生、用小正方形换25元这样的操作。从而拓展了学生对25×12这个算式实际意义的理解，也拓展了学生对长方形面积的深入理解。

（5）变式算式为25×（10+2），看了这个算式你能想到哪个图形？试着画一画。

如果学生能画出右图这样的图形，说明学生对于长方形的面积与算式之间真正建立起了关联，此时教师再引导学生理解算式的实际意义，就会进一步深化学生对于长方形面积的理解。

（二）可以将画长方形解决问题作为补充课程分段实施教学

根据本次课例尝试情况，笔者建议分三段实施教学，安排如下。

1.安排在三下学习了长方形面积之后

当学生学习了长方形面积计算，并能够比较熟练地解决已知长、宽、面积的任何两个量求第三个量的问题的基础上，设计第一次学习。本次学习主要是画长方形图解决长方形本身的问题。可设计这样的问题：一个长方形花坛，长8米。如果长增加2米，面积就增加6平方米。原来这个花坛的面积是多少平方米？

通过画长方形解答这样的问题，教师强调在画图时要表示出“已知信息”与“所求问题”，帮助学生初步积累据题画图以及依图析题的经验。

2.安排在四上学习了单价×数量=总价、速度×时间=路程两个数量关系之后

这个内容的编排类似于本课例所讲的内容。即重点研究不具有“长方形元素”的内容如何通过画长方形图解答的问题。因为有了第一段的画图经验，所以在第二段的学习中重点解决遇到一个表示两量之积的问题时，首先要明确长表示什么，宽表示什么，面积表示什么。然后再利用在第一段学习到的画图经验据题画图、依图析题。进而将不具有“长方形元素”的内容与长方形面积之间建立关联，促进学生对长方形面积的深入理解。

3.安排在五下“分数的加法和减法”单元的“喝牛奶问题”之后

五下的“喝牛奶问题”虽然也是通过画长方形图分析解答的，但该内容其实并不是笔者所要研究的画长方形解决问题的范畴，因为它不涉及要明确长、宽、面积所表示的量，就是用长方形表示这杯牛奶。

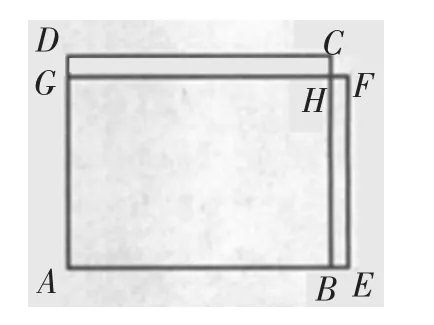
之所以安排在这个内容之后，就是使学生感觉到画长方形能解决像“喝牛奶”这样的稍复杂问题，同时希望在此基础上进一步拓宽学生的视野，因此所涉及的问题要比第二段的再略微复杂和多样一些，让学生进一步感受画长方形解决稍复杂问题的优越性。比如计算676×678-675×679，具体分析说明如下。

如下图，用长方形ABCD表示676×678的积。长AB表示678，宽AD表示676。长增加1，宽减少1，可得长方形AEFG，即AE=679，AG=675。从图中可看出676×678-675×679的差其实就是长方形ABCD与长方形AEFG的面积差，因为它们有公共的长方形ABHG，因此，差就是长方形GHCD与长方形BEFH的面积差。所以676×678-675×679=678×1-675×1=3。