数（shù）源于数（shǔ），意义始于表征——基于前测定位下“小数的意义”一课教学思考

□ 张伟明

一、缘起

“小数的意义”这一课内容被编排在人教版教材四年级下册，是小数意义的再认识，教材在学生认识小数现实模型的基础上，借助长度单位及其现实意义，与十进分数之间建立联系。笔者试着请教了相关年级的教师，无一不感慨，“这节课太难上了”。深思其原因，整数的位值概念和分数的意义制约着学生对小数意义的深度理解。从本质上来说，除了无限不循环小数外，其余的小数都是一种特殊的分数，分数的意义可以从分割与合成的角度来解释。但就数的表示形式来看，小数与整数有着更为紧密的联系，这主要是因为小数和整数都遵循十进制计数法的位值原则。

学生对小数的理解究竟有多深？小数与整数的表征如何来建立？小数与分数的联系如何可以更紧密？教师应该怎样引导学生认识小数的本质？带着这些问题，笔者精心设计了问卷，对学校四年级共160名学生展开了学情调查，并在此基础上形成对“小数的意义”一课的教学思考。

二、部分测评题及测评结果分析

（一）小数的认读起点及分析

测评题1及结果分析：

生活中你见过小数吗？请你写出一个带单位的小数，并解释这个小数所表示的意思。

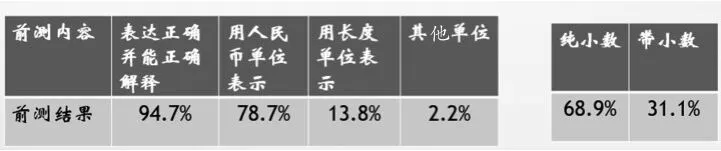
从结果上看，学生在生活情境下对于小数的含义的理解是到位的，对于纯小数且一位小数最熟悉，教师可以把课堂的重心放在两位小数的构建及多位小数的推理上，适当增加部分带小数的相关内容。学生对于小数的生活经验大多来源于标价，如人民币单位，可以适当增加其他单位如“米”等的理解，促进学生对于小数意义的完整建构。

（二）小数与整数、分数的联系分析

测评题2、部分学生答卷及结果分析：

你能用自己喜欢的方式表示出0.1和0.01吗？

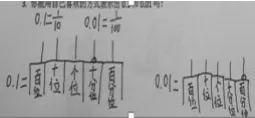
图1

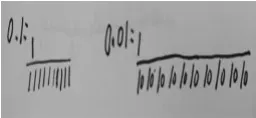
图2

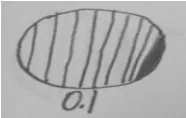
图3

看似丰富的表征背后不难读出学生对于这两个代表小数计数单位的数存在认识上的一种缺失。从上图我们读出学生对于小数都有了一定的了解，所以他们对于0.1和0.01都能用自己的方式（文字、数字、图形等）进行表征，图1是一种简化版的图，学生说，0.1是1占了10个1中的1份，0.01是1占了10个10中的1份，与分数进行了一定的建构。图2学生借用的是计数器模型，在计数器上设了十分位、百分位，就能轻松表示小数，这样的学生对于小数与整数的联系非常清晰。图3则借助了图进行表征，学生知道要把整体分成10份，但对于平均分并没有概念。整体上看，学生对于分物的整体认识不充分，对于均分概念比较模糊，大部分学生对小数的理解仍停留在小数形式表面，对于小数本质意义的理解还需多种形式辅助。

（三）小数与整数、分数的联系分析

测评题3、部分学生答卷及结果分析：

用合适的数填一填。

比0.1大，比0.3小的数有（ ）

0.5+0.08=（ ）你的解释_____________

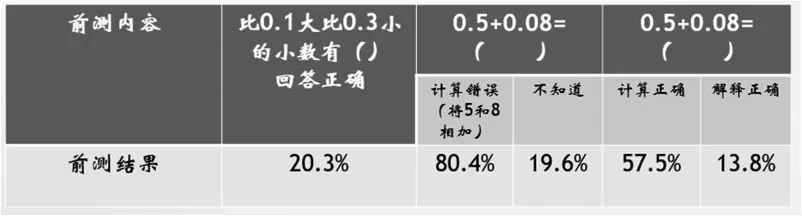
图4

图5

图6

学生对于小数的意义的理解还存在一个理想与现实的差距，近80%的学生认为比0.1大比0.3小的数只有一个0.2，即对小数的本质属性——小数的稠密性缺乏完整的体验，对于小数的产生及其必要性缺少概念，整数知识对小数意义的学习有着很大的帮助，学生能通过以往整数学习经验同小数进行类比，结果显示有57.5%的学生能通过整数知识的类比找到正确的结果，但只有13.8%的学生能以计数单位的视角进行正确的解释，而在不能正确计算的42.5%的学生中，有80.4%的学生把5和8相加，反映了学生对于计数单位的理解还不到位。

三、策略思考

基于前测对于教学的定位，笔者形成了对“小数的意义”一课的思考。

（一）以“整体”为入口，表征小数

张奠宙教授认为：“引进小数是为了表示小于‘单位1’的量，除0之外，自然数中最小的是1，所以自然数不能表示小于1的量。小数是分母为10，100，1000……的一类特殊分数。小数十进制位值原则记数法，满十进一，但分数不是。”因此作为均分标准的“1”对于认识小数及其意义有着至关重要的作用。而对于这个“1”的理解，以及对“1”充分理解后的表征则是走向小数意义理解的第一步。

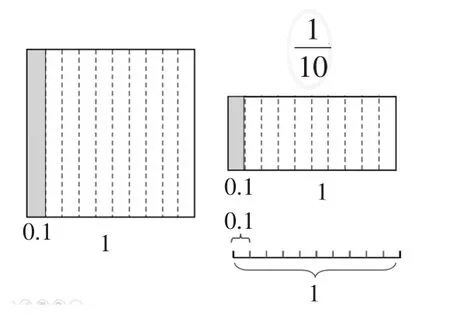
笔者认为建构起以面积、线段、数轴等模型多元感知“1”，同时结合具体的情境激发学生对小数产生实际的共鸣。譬如在表征0.1时，可以先让学生自主说一说0.1具体可以表示什么，学生可以把生活经验中的0.1元、0.1千克、0.1米等抽取出来，并对0.1和1元、1千克、1米进行对比，从而形成对小数的初步认知。接着让学生在面积、线段“1”中表征0.1，帮助学生建立对不同“1”形的认知，从而为感知小数的本质意义，建立小数与整数、分数的联系，抽象出数学意义上的0.1奠定基础。在这些模型的堆叠、运用、建构中，图、数学结构、现实生活情境，通过生活语言、图示语言和数学语言相互转化，从而丰富教学的内涵。

（二）以“数数”为突破，展现过程

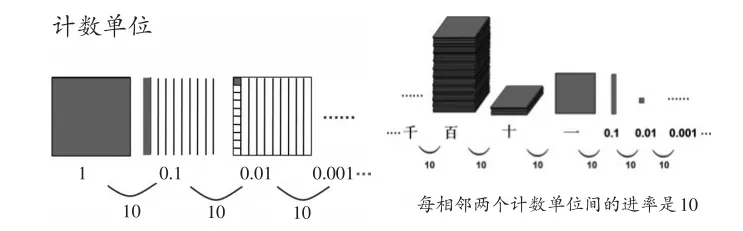
华罗庚曾说：“数（shù）源于数（shǔ）。”数（shù）的本质其实是数（shǔ），而数（shǔ）的本质在于计数单位，如整数，我们可以一个一个数，十个十个数，百个百个数，个、十、百就是计数单位。小数和分数亦是如此，通过数数，展开教学过程，在序列增加或减少中，凸显计数单位，培养数感，丰富学生数概念。

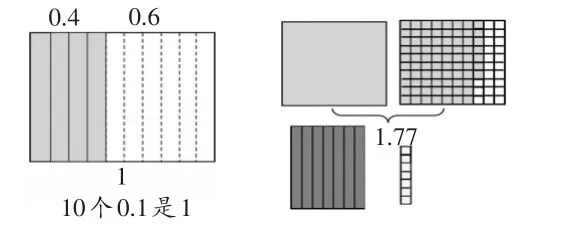
因此，笔者建议在教学中应关注作为计数单位的0.1及0.01的认识，把小数的意义和对小数的建构建立在数计数单位上来。在表征出0.1后，可以借助于数数巩固对0.1的认识，如在面积模型中从0.4开始数数到整数1，验证10个0.1是1，建立“1”与0.1在形上的联系。而在对本课的难点两位小数的突破上，还是以数数为基础，让学生在实际情境（如身高）0.01中或0.01的增加中深刻认识两位小数的计数单位是0.01，在数到相同的数如1.77时，感知一位小数与两位小数的区别，在数到1.80时体会一位小数与两位小数的联系。为比较一位小数与两位小数的本质，进而推理产生三位小数乃至多位小数，建构起小数体系，夯实了基础。学生在数数中所经历的十等分、百等分及计数单位累加的过程，深化了对小数意义的认知，形成了对计数单位、数位等抽象意义更深刻、个性化的认识和理解。

（三）以“分割”为深化，促进内化

维果茨基说：“了解概念形成的过程，即可把握住儿童认知与思维的过程。”对于数概念的理解也应遵循数概念的形成过程。即帮助学生在无限分割中逐步建立小数概念，体会小数因测量、分物、计算而产生需要，深度理解小数的稠密性，从而促进自身的认知，提升数学思维。

笔者认为小数的产生其实质是整数不够表示。当整数不够表示时，把整数平均分成10份，每1份是0.1，于是就产生了一位小数，当一位小数不够表示时，就把0.1平均分成10份，每1份就是0.01，于是就产生了两位小数。多位小数亦是如此。借助面积、立体、数轴模型十等分再十等分，学生不断感受细分的过程，逐渐体会两个小数之间还存在着无数个小数。以这样的分割操作引入，学生在分一分、画一画、说一说、数一数等活动中发现小数产生的实际需要，体验具体到抽象的理解过程，从而刻画出小数的稠密性。在这样的学习活动中，学生对于整数、分数自然进行了联系，而数数又很好地弥补了学生意义概念上的缺失，指向于学生对于数的本质理解，打破了学生原有的数的体系，丰富了数系的内涵，而更为关键的是学生习得数产生的基本活动经验，为后续新的数的学习埋下了种子。

（四）以“文化”厚实，培育素养

《义务教育数学课程标准（2011年版）》指出：“数学是人类文化的重要组成部分，数学素养是现代社会每一个公民应该具备的基本素养。”可见，数学、文化、素养本身就可以进行有机结合。在数学的课堂里，以文化人，用文化来培育人，让素养得以真正发生，是“小数的意义”这一课所期望达成的另一高度。

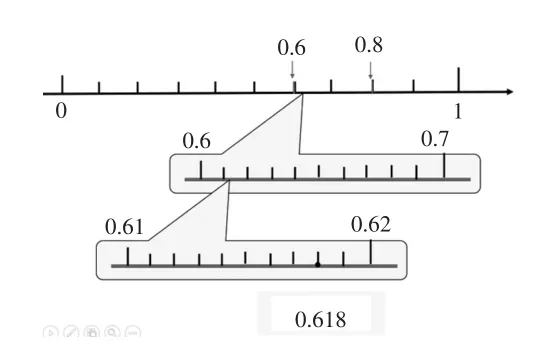
笔者认为，可以让数学在人文科学、自然科学领域找到原型，用学生所熟知的小数，如圆周率π、黄金分割率0.618等展开设计，开阔学生的视野，让素养伴随着文化自然发生。以0.618为例，给出一条0～1的数轴，让学生来猜数。在学生的猜测中谜底逐步揭示，学生在数线的无限逼近中实现对小数意义的深度抽象认识，推理出数轴上的点是稠密的，并且是连续的，任意两个无限接近的点之间的线段仍然可以不断地细分，从而继续产生无数个点的特性，与此对应的小数也是无穷无尽的，从而建构起对小数本质意义的理解。在数学素养诸如抽象、推理等概念的建立的同时，学生对0.618这个古老分割率的认识得到了提升。