善用知识联系 加深数学理解——“积的变化规律”教学实践

□ 俞世祥 朱 萍 洪巨波

“积的变化规律”是乘法计算中自然存在着的规律，即当一个因数不变，积与另外一个因数存在着正比例关系。这一种关系，在二年级学习乘法口诀时学生已经有所体会，如“一五得五，二五一十”。其中因数5不变，另一个因数乘2，积也乘2，反之，另外一个因数除以2，积也除以2。但是，由于受当时学生思维水平的限制，并没有引导学生做这样的探究。到了四年级上学期，学生对“积的变化规律”已经有了较为丰富的认识基础，教师可以引导学生通过对计算题的观察，发现规律、总结规律、应用规律，并渗透函数思想。

一、抽象概括，总结规律

在相应题组计算的过程中，让学生自主地发现“积的变化规律”，是基本的教学思路。同时，不同的学生对于规律发现的水平是不一样的。因此，教师可以在计算后让学生充分表达自己的发现，有层次地展示学生的发现，在交流互动过程中逐步发现规律、总结规律。

（一）计算观察，获得结论

课始，教师出示如下两组计算题，并提出问题：观察这两组计算题，你有什么发现？

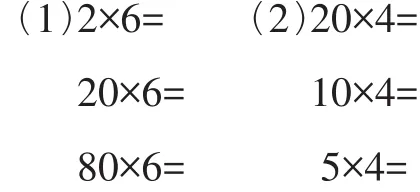
对于这两组题目，笔者预设，学生在观察时会有两种发现，一种发现是定性的，即每一组中的两个算式间一个因数不变，另一个因数变大（或变小），积也变大（或变小）。另一种发现是定量的，即一个因数不变，另一个因数乘（或除以）几，积也乘（或除以）几。当然，学生在表达第二种规律时，一般会用具体的数据进行展示。在自主发现规律阶段，这两种发现应该都是正确的，都可以成为后续的学习资源。

（二）交流互动，分析结论

不同认知水平的学生，发现的规律也是不同的。整体展示学生发现的几种典型的规律，在交流比较的过程中，逐步分析结论。

教师首先展示围绕第1组题发现的规律。

（1）一个因数不变，另一个因数变大，积也变大。

（2）一个因数不变，另一个因数乘几，积也乘几。展示上面的两种发现后，教师追问：它们是由哪一组计算题归纳得到的？并在观察发现第一种规律是正确的基础上，进一步提问：第二种发现正确吗？你能够举例说一说吗？依据学生的说法，得到如图1的板书。

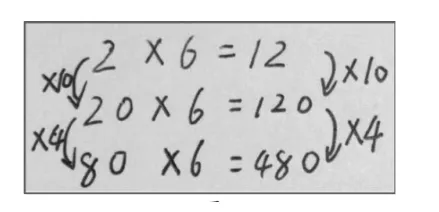
图1

进一步分析，这两种规律，哪一种规律更符合实际。为什么？逐步引导学生认识到，第一种规律只是说明变化的情况，第二种规律还说明了具体的变化。所以第二种更符合实际。在此基础上，依据这一种经验，再对第2题组发现的规律进行修正。

（三）举例验证，完善规律

上面的发现，还只停留于一个题组的归纳。鉴于此，可以让学生再举一组同类的算式，验证总结的规律是否也同时成立。

在学生举例的基础上，教师举出如图2的例子。请学生分析图2中的算式“同时除以0”是否有意义，从而进一步完善原来总结的规律。

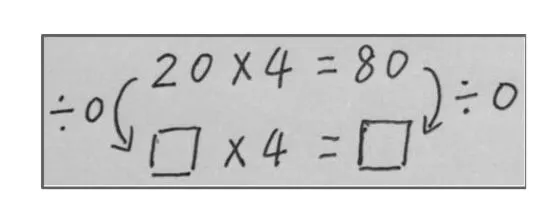
图2

观察与分析、抽象与概括、猜想与验证是学生发现数学规律的基本方式。因此，教师在提供学习材料之后，应该让学生有充足的独立探究与交流反馈的时空，让数学规律的发现过程成为学生数学学习经验的积累过程。

二、回溯旧知，温故知新

“积的变化规律”的发现与总结，来自对已知的乘法题组。总结出规律后，引导学生进一步回顾与“积的变化规律”有关的旧知，并用积的变化规律对新知进行理解，从而渗透函数思想。

（一）乘法口诀的回顾

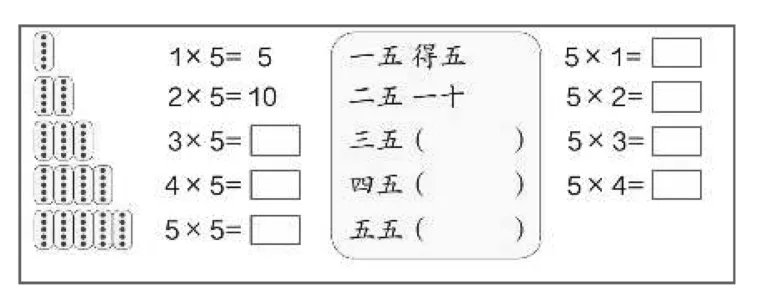
图3

教师出示二年级上学期学习乘法口诀时的一则教材内容（如图3），并提问：这是我们二年级学过的关于“5的乘法口诀”，你能够发现其中含有的“积的变化规律”吗？

学生指出，可以发现其中5不变，另一个因数乘2、3、4、5，积也分别乘2、3、4、5。

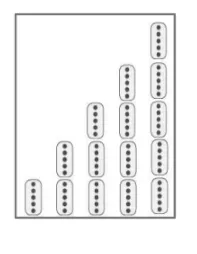
图4

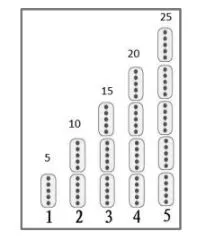
图5

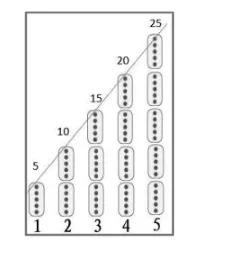
图6

之后，教师把图3进行调整，变成了如图4的形式，然后追问：从左往右看，各有几个5，积是多少？学生回答后得到图5。最后教师添上一条直线（见图6），让学生直观感受积的变化过程。

通过上面这些图的演示，学生直观地感受到5的个数与积的变化过程，整个教学渗透了正比例的函数思想。

（二）整十、整百数乘一位数口算的回顾

整十、整百、整千数乘一位数是多位数乘一位数的基础，当时教学时，是通过数的意义来说明算理，并通过题组比较，总结简便算法。在学习了“积的变化规律”后，可以引导学生从积的变化规律的角度来阐述算理。

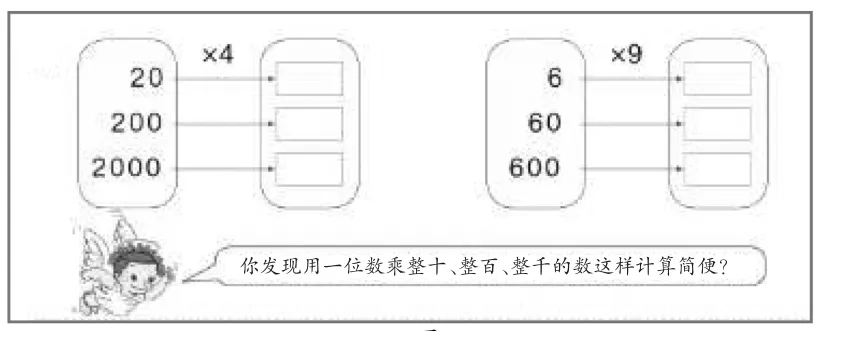
图7

教师出示图7，提问：想一想，你能够用“积的变化规律”来解释简算的道理吗？学生回答后，再让学生编制这样的一组题目，让同桌完成。

在数学学习时，许多规律在发现之前已经在具体的数学情境中应用了，如在学习运算定律之前，在计算与解决问题时已经被多次应用了。因此，在总结出相关的运算定律后，可以选择合适的素材进行回顾反思。

（三）整十、整百数乘一位数笔算的回顾

在学习多位数乘一位数的笔算乘法中，当多位数末尾有零时，已经学习了用竖式计算，当时更多地是从口算乘法中进行形式化的迁移，并没有做算理上的解释。在本节课中，可以出示如图8的例题，让学生用“积的变化规律”来解释算理。

例6呈现的是计算方法上的优化，是学习三位数乘两位数例2的基础。出示本题，除了重新解释算理外，也为教学三位数乘两位数末尾有零乘法做好铺垫。

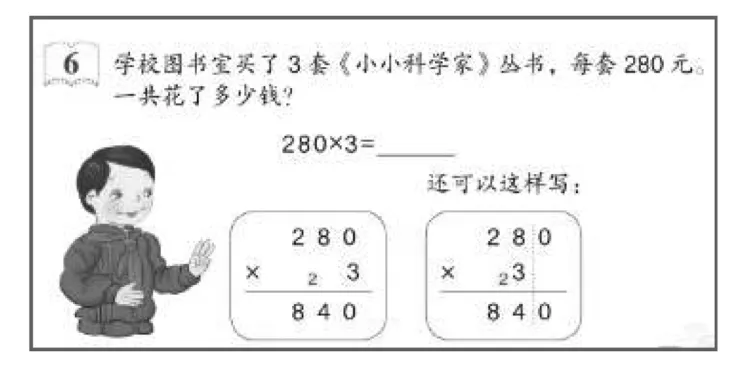
图8

三、以旧促新，综合应用

在数学学习过程中，有许多新知是在旧知的基础上就某一个方面适当地拓展，如从“两位数乘两位数”到“三位数乘两位数”；有的是对旧有的问题在新的知识背景下进行重新思考，如从“归一应用问题”到“正比例应用问题”。对于前者，我们可以把“新授课”当作“练习课”来上，对于后者，我们则需要更新原有的思维方式，将思维方式进行优化与提炼。在本节课中，这两个方面的例子都出现了。

（一）渗透类比思想，学习“几百几十乘几十”的笔算

显然，人教版四年级上册“三位数乘两位数”例2（如图9），与“整十、整百、整千数乘一位数”笔算是同一类型的。因此，回顾了后者，并用积的变化规律进行算理重构后，我们顺势而为，出示了如下的题组，让学生尝试笔算。

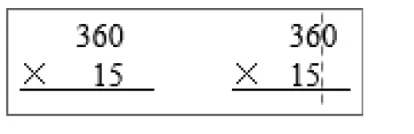
图9

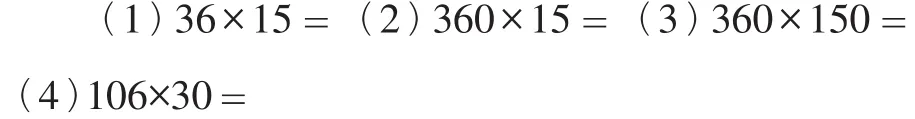
这四个题目，前三题相互联系，第（1）题是两位数乘两位数，第（2）（3）题是在第（1）题的基础上出现了积末尾有零的情况。在学生计算之前，可以引导学生对这四道题进行比较，让学生先摆出两个因数相乘的竖式，然后说一说自己计算的思路，再整体计算。如其中的第（2）题，学生会有如图9的两种摆法。整体展示后，让学生说一说哪一种摆法计算时会简便一些，这样计算的理由是什么？通过交流讨论，统一竖式的摆法后，自主计算，反馈纠错。反馈时可以特别讨论第（3）题两个因数末尾均有一个0时积为什么要添上两个0。

这样的编排结构，把因数末尾有零的“三位数乘两位数”的笔算作为“积的变化规律”的应用，更有利于促进学生利用类比思想解决问题。

（二）利用几何直观，学习求“长方形扩大后的面积”新方法

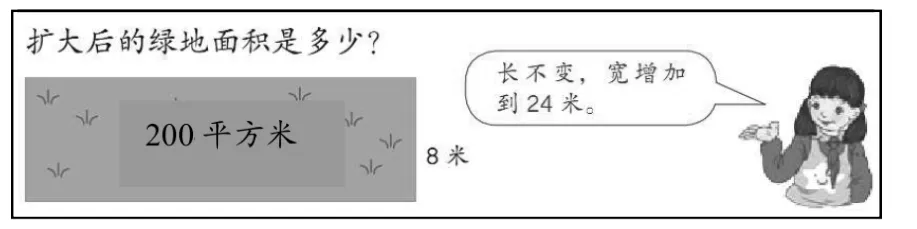
图10

如图10，是利用“积的变化规律”解决实际问题的一个很好的例子。但是，在独立完成时，大多数学生是根据长方形的面积与宽先求出长方形的长，再用长乘增加后的宽来求出“扩大后的面积”。如何引导学生根据增加后的宽与原来的宽的倍数关系来求扩大后的面积呢？采用几何直观是一种好方法。

在实际教学时，教师先请学生把题目中的信息用图画出来（如图11），然后再依据图示来解决问题。这时，大部分学生能够同时用如下两种方法计算，其中第二种方法就是“积的变化规律”的具体应用。

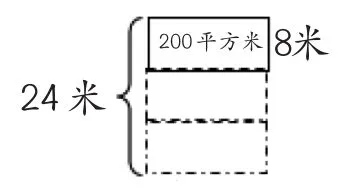
图11

方法1:200÷8×24

方法2:200×（24÷8）

把文字信息用图来表达，可以发挥“几何直观”的优点，发现更加合理、简捷的解决问题的思路。

（三）借助表格信息，拓展“积的变化规律”

前面学习的“积的变化规律”，实质上是正比例函数的模型。那么，当积不变时，两个因数又会怎样变化呢？这既可以看成“积的变化规律”的拓展，也可以表述成“因数的变化规律”，即反比例函数的模型。就简便运算而言，运用这一个模型，在后续学习如“1800×25”这类题目的简便计算时，就可作为简算的依据。

为了让学生探究这一种规律，我们设计了如下一份表格。

因数因数积100 6 10 60 50 12 200 3

先请学生计算出前面4组因数的积，然后请学生说一说有什么发现。根据“积的变化规律”的学习经验，逐步概括出“因数的变化规律”，并依据发现的规律，填写最后一组因数和积。

综上可以体会到，数学知识间是有内在联系的，教师在分析一个课时内容时，通过回溯，不仅可以了解学生的学习基础，还可以对原有知识进行进一步分析、提炼，真正做到“温故而知新”；同时，还可以沟通后续学习的内容，适时渗透数学思想方法，积累数学活动经验。