单元整体设计 完善学习序列
——以“三位数乘两位数”的单元教学为例
□陈 芳 邵汉民
小学数学教材由一个个相对独立的单元构成,同一单元中的新知又是按照一定的逻辑顺序编写,从而可以在单元学习的过程中让学生形成良好的认知结构。同时,在教学中,我们也发现,有一些单元的教学顺序如果能够做适度调整,就可以让各个课时之间的逻辑关系更加符合新知学习的认知规律。因此,我们可以从单元整体设计的视角审视单元内的课时教学内容,从分析原有的单元学习序列入手,发现可以改进之处;重构新单元学习序列,实现“部分之和大于整体”的目的;最后从课时设计出发,适当添加新的课时教学内容,让每一个课时的教学目标更加完善。下面以人教版“三位数乘两位数”的单元整体设计为例,谈谈具体的做法。
一、分析原有的单元学习序列
分析单元学习序列,可以从单元结构分析入手。首先,厘清单元有哪几个学习板块,这些学习板块间又是怎样的关系;其次,进一步分析各个板块需要怎样的学习基础;最后,从完善各个板块间的逻辑关系入手进行辨析,为重构单元学习序列做准备。
(一)单元结构分析
逻辑性是数学重要的特征。体现在单元中,是指一个单元中的数学知识的学习序列呈递进关系。如三年级上册“倍的认识”这一个单元,学习序列是“倍的认识→倍的应用问题”,在建立倍的概念的基础上,然后在具体情境的应用中,总结“求一个数是另一个数几倍”和“求一个数的几倍是多少”两类应用问题的数量关系。前者是后者学习的基础,两个板块不可以交换。
而2011年版的人教版“三位数乘两位数”这一个单元比较特殊,它的三个板块虽然都是关于乘法的内容,但又是相互独立的,呈并列关系,如图1。

图1
第一个板块是例1、例2,即“三位数乘两位数”笔算乘法。两个例题是按一般到特殊的形式编排,即例2一般是在例1“三位数乘两位数笔算”的基础上,学习因数末尾有0或第一个因数中间有0的两种特殊的乘法笔算;第二个板块是例3,即积的变化规律,通过计算有联系的乘法题组,观察、分析、概括出规律;第三个板块是例4、例5,即乘法中两个常见的数量关系,通过举例,概括得出更为一般的数量关系。
这样的单元结构也不是特例,如四年级上册的“除数是两位数的除法”中的三个板块,其中“口算除法”板块与“笔算除法”板块是递进的,而第三个板块“商的变化规律”又是独立的。
那么,这样的单元,是否可以通过单元内部结构的重组,增强板块间的内在联系,体现单元的结构性与逻辑性呢?
(二)学习基础分析
学习基础包括两个方面,一是已经学习的数学知识,二是已经有的生活经验。呈递进关系的数学新知,前者的学习往往就是后者的学习基础,或者是主要的学习基础。但是,并列关系的单元,各个板块的学习基础往往是独立的。
如“三位数乘两位数”的三个板块的学习基础就是相互独立的。从图1可以清晰地发现,第一个板块的学习基础是“多位数乘一位数”“两位数乘两位数”,前者提供的是分步积的计算方法,后者提供的是算理与法则。因此,可以用类比迁移的思想方法让学生自主探究;第二个板块的学习基础是对有联系的乘法计算题组的观察、发现与归纳;第三个板块则是对原有的用乘法解决问题时的数量关系进行分类与概括。
所以,这三个板块的学习,都可以提供相应的学习材料,让学生进行自主尝试、自主探究,并通过交流反馈的形式总结法则、探究规律。
(三)逻辑关系辨析
逻辑关系辨析就是指在分析单元结构与学习基础后,探究原来教材单元学习序列中的不合理之处,为重构新的单元学习序列寻找实践的依据。
经探究可以发现,第一个板块中的例2因数末尾有零的乘法,虽然可以由“多位数乘一位数”的同类笔算乘法进行迁移,但是在之前学习时也只是法则上的规定,并没有算理上的解释。而第二个板块“积的变化规律”恰恰可以作为其算理上的解释,因此如果能够调整这两个板块的顺序,更有利于“例2”算理的总结与理解,如图2。
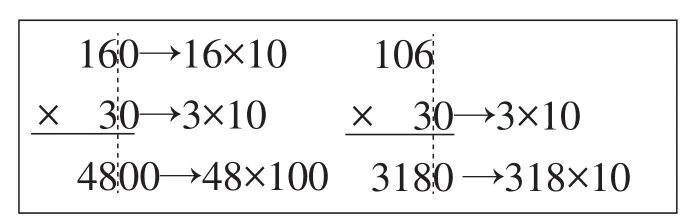
图2
同时还可以发现,第三个板块如果能够前置到第一个板块前,即成为新的第二个板块,则如例1的数量关系,可以用“(火车的)速度×时间=(到北京的)路程”来概括。同时,“积的变化规律”包含了正反比例函数的模型(如图3),在学习了这一个“模型”后,再来分析乘法的数量关系,也可以从“函数”的视角设计问题,如知道“单价”后,结合具体例子,分析当“单价”不变时,总价如果增加、数量会怎样变化。
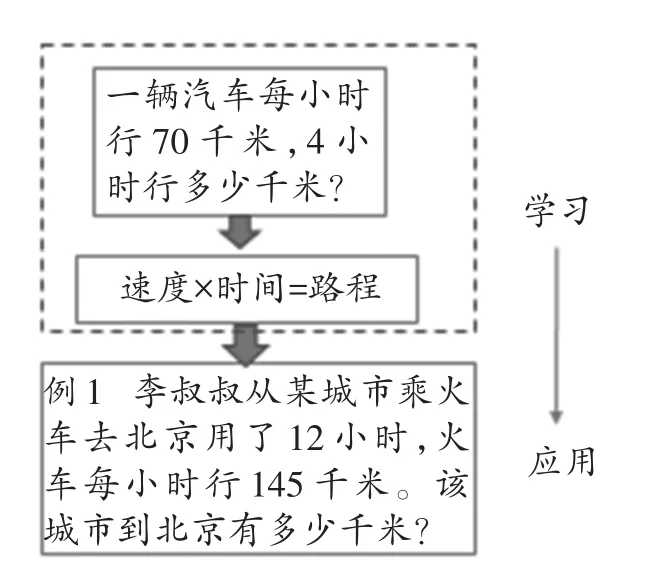
图3
因此,通过单元板块间逻辑关系的辨析,可以使各个板块之间的逻辑关系更加密切,让原来相互独立的板块,通过合理调整,成为有逻辑关系的单元学习序列。
二、重构新的单元学习序列
对原单元进行分析与辨析,既可以梳理出学习序列,更可以揭示重构新的单元学习序列的必要性与可行性。重构新的单元学习序列,可以以调整单元学习序列为基础,整合单元学习内容,并选择合适的切入点进行基于单元的课程拓展。
(一)调整单元学习序列
调整单元学习序列可以分为三类。一是重新构建板块,即把单元中的新知重新组织,形成新的板块。二是板块内的调整,即把某板块内的学习序列进行调整。三是对各板块的学习顺序进行整体调整。
“三位数乘两位数”主要采用第三类方式进行调整,即调整后的第一个板块为“积的变化规律”。第二个板块是“常见的数量关系”,第三个板块是“三位数乘两位数”。并且努力实现前一板块的学习内容在后一个板块学习时进行合理的应用,如图4。
调整单元学习序列,可以更好地构建起单元逻辑结构,让前一节课学习的知识成为后一节课的学习基础,前一节课获得的学习经验,在下一节课中得到应用。
(二)整合单元学习内容
在调整学习序列的基础上,还要考虑如何进行单元学习内容的整合,注重前期渗透,提高课堂教学实效。
如在总结了“积的变化规律”后,教师可以让学生回顾原来的“两位数乘两位数”中因数末尾有零的竖式计算,让学生用新学习的知识进行解释。或者可以直接出示例2中末尾有零的“三位数乘两位数”的题目,让学生想一想,可以怎样摆竖式,如何计算?这样,“三位数乘两位数”例2中的两个计算题就可以应用转化思想与积的变化规律得到解决,如图5。

图5
整合单元学习内容,适当打破原有的编排结构,以符合学生的认知规律,让每一个课时重点突出,相关内容联系紧密。
(三)拓展单元学习内容
通过整合单元学习内容,有时候可以节省出课时,用节省的课时进行课程拓展,可以更好地巩固新知,拓展思维。
如本单元通过整合,把例2作为“积的变化规律”的应用,节省一个课时。因此,我们把教材中练习八第12题(如图6)作为数学课程拓展的素材,让学生通过多种尝试,逐步发现乘积最大的算式特点。

图6
在人教版教材中,有不少带“*”或“?”的思考题,这些题目如果在正常的课时教学中进行练习,学生解决问题的时间相对较少,不能很好地体现这些题目的教学价值。因此,教师可以采用“一题一课”的形式,让它们成为拓展学生数学思维的好材料。
三、添加新的课时教学内容
基于单元的教学重构,也可以在此基础上对某些课时的教学内容进行重新编排,调整或增加一些教学内容,以帮助学生更好地学习数学知识,发展数学思维。
(一)在“积的变化规律”中沟通新旧知识间的联系
“积的变化规律”是乘法计算中自然存在的规律,即当一个因数不变,积与其中的一个因数存在着正比例关系。这一种关系在之前的乘法学习中多次出现。因此,在“积的变化规律”的教学中,除了前文指出可以整合例2的内容外,也可以对体现“积的变化规律”的旧知进行系统梳理,让学生体会到数学学习是一个不断积累经验与抽象概括的过程。这样的例子在数学新知学习中是很常见的,如“乘法分配律”“商的变化规律”等。
(二)在练习复习课中增加新的数量关系
在日常生活中,除了有关“单价”与“速度”的两个数量关系,还有一个常见的关系式“工作效率×工作时间=工作总量”(以下简称“有关‘工作效率’的关系式”)。它可以看成有关“速度”的数量关系的变式,在学生学习了有关“速度”的数量关系后,添加有关“工作效率”的关系式来解决问题,让学生在比较中总结出有关“工作效率”的数量关系。
(三)在“三位数乘两位数”教学时感受整数笔算乘法的一般化
“三位数乘两位数”的算理与算法迁移于“两位数乘两位数”,在此基础上,可以进一步追问假如是“四位数乘两位数”“三位数乘三位数”又应该怎样计算?整数乘法都是怎样笔算的?在解决以上问题时实现笔算乘法的一般化。同时,介绍“你知道吗?”中的“格子乘法”,进一步体会笔算乘法的算理是因数的分解相乘后再相加,并经历了由繁到简的过程。
(四)在“常见的数量关系”教学时渗透函数思想
“数量关系”反映的是有关联的量之间的运算关系。进一步理解,如果把“三个量”称为“三种量”,就可以从“常量思维”转变到“变量思维”,“函数思想”的渗透就可实现了。在教学“单价、数量与总价”“速度、时间与路程”这几个数的关系时,可以突出对“单价”“速度”(包括“工作效率”)的理解。“单价”体现的是商品的价格高低,同一种商品,当“单价”一定时,数量增加,总价也增加;当“总价”一定时,数量如果需要增加,那么“单价”就要下降;在“速度、时间与路程”(包括“工作效率、工作时间与工作总量”)中也可以发现同样的变化规律。
总之,我们的单元整体设计经历了“分析”“重构”与“添加”这三个步骤。通过分析,指出原单元结构中存在的问题;通过重构,意在构建更加合理的教学序列;通过添加,可以使每一课时的教学目标更加丰盈。在此基础上,结合具体的单元,在实践研究时做出调整,以更好地构建起基于学生认知规律与数学学科逻辑的单元教学体系。

