体认数量关系 渗透函数思想
——有关“单价”的数量关系教学实践
□ 杨丹华 吴月芳
人教版四年级上册关于“单价”与“速度”的数量关系,是教材中唯一单独教学的两个数量关系。教材首先安排了两个与“单价、数量与总价”有关的具体问题,寻找到相同点后进一步抽象概括,形成“单价×数量=总价”这一个数量关系。除此之外,如何理解“单价”的含义?在理解、总结与应用这一数量关系时,可以用怎样的策略渗透函数思想?笔者带着这些问题进行了教学实践。
一、观察比较,理解“单价”内涵
显然,在“单价×数量=总价”的关系式中,“单价”是其中的核心概念。“单价”是标明商品价格,在商场里每一种商品都有自己独有的“单价”,学生在生活中已经有了很多的经验积累。
(一)观察标价,理解标价的结构
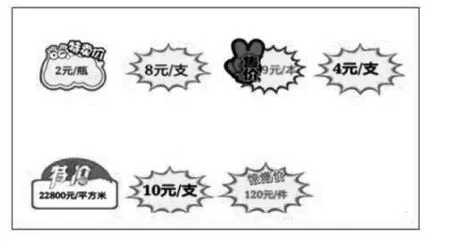
图1
课始,教师出示一组商品标价(如图1),提出问题:这是7件商品的标价,请你仔细观察,哪几个标价可能是同一类商品,为什么?
这几个标价,均采用了“复合单位”的方式表示。教师通过提问,让学生对单位进行分析比较,可以发现,每一个标价都有“元/□”这样的结构。同时“8元/支”“10元/支”和“4元/支”的单位又是相同的。
因此,学生在回答上述问题时,需要分析每一个标价的结构,从中推导出每一个标价的含义。
(二)猜测商品,沟通标价与商品的联系
上述标价所对应的商品是日常生活中常见的。学生依据生活经验,可以猜测相对应的商品,从而沟通标价与商品之间的联系,更好地理解“单价”的内涵。
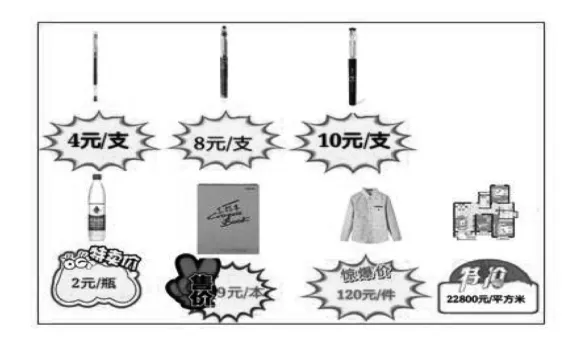
图2
教师把相同单位的三个标价放到了一排,请学生猜一猜,可能是哪一类商品。然后出示图示,发现原来是三种不同的水笔标价,再猜一猜其他几个标价分别是什么商品?学生猜测并说明理由后,教师逐步把图1补充成图2。
最后,以具体的商品标价为基础,教师总结:像这样每瓶矿泉水的价格,每支水笔的价格,每件衣服的价格……我们称之为商品的“单价”。
(三)比较标价,发现标价之间的联系
同样的商品,由于包装不同,商品单价的标价形式也会发生变化。
因此,为了更深入理解“单价”的内涵,我们还可以比较同种商品不同包装下的标价,进一步体会单价的内涵。
教师出示图3的标价,请学生猜一猜,它可能是哪一种商品。

图3

图4
学生猜测后出示图4。同样是“农夫山泉矿泉水”,为什么有两个单价?你还能够举出这样的例子吗?
以上三个教学环节,学生先在比较中认识商品标价的结构,再由商品标价猜测具体商品,最后得出由不同标价可表示相同商品。围绕“单价”内涵环环相扣,层层推进,充分利用了学生的生活经验。
二、列举实例,概括数量关系
理解了“单价”的内涵,“数量”“总价”以及由这三个概念构成的关系式就可以在具体应用中逐步概括。并且,通过题组分析,发现各个量之间的变化规律,由单纯的数量关系转变为渗透函数思想的关系式。
(一)纵向解决问题,概括基本数量关系
纵向解决问题是指利用同一个单价,改变其中的数量,求总价的过程。在解决这样的题组后,再引导学生观察比较,概括“数量”“总价”与“单价×数量=总价”之间的关系。
教师创设购物情境,提出问题:买单价是8元/支的水笔2支,需要多少钱?20支呢?200支呢?

图5
学生独立列式解答后校对。然后教师进一步引导学生概括,这里的“2支”“20支”“200支”叫作商品的“数量”,“16元”“160元”“1600元”是购买商品总共需要花的钱,叫作“总价”。在此基础上进一步追问:你能够用“单价”“数量”“总价”概括出这三个算式的共同的关系式吗?学生回答后形成如图5的板书。
(二)横向解决问题,灵活变式数量关系
横向解决问题是指在得到基本关系式后,通过改变已知条件与所求问题,在解决具体问题的过程中概括出新的数量关系的过程。在解决问题的过程中,逐步形成利用关系式解决问题的一般思路,即先抽象概括信息与问题,用“单价”“数量”“总价”表示,然后列出关系式,再列式并解答。
教师在总结了上述数量关系后继续提出问题:
王老师到商店去买一些水笔,带去的钱正好可以买单价8元/支的水笔30支。王老师想买60支水笔,需要选哪一种水笔?
这是一个可以用多种思路解决的问题。首先可以用“单价×数量=总价”求出王老师带的钱数,即“8×30=240(元)”,这是基本数量关系的具体运用。要求“选哪一种水笔”就是求新的单价,可以有三种思路。第一种是“总价÷数量=单价”,即“240÷60=?”,当列出这一种方法后,学生发现无法计算,思路需要改变(当然有部分学生能够计算);第二种是“总价÷单价=数量”,即“240÷4=?”,如果商是60,单价就是“4元/支”;第三种是“单价×数量=总价”,即“4×60=?”,如果积是240,那么单价就是“4元/支”。
解决同一个问题用多种思路,逐步概括出基本关系式的变式。同时,让学生感受到,在解决问题时要灵活变换数量关系,形成基本数量关系与数量关系变式的体系。
(三)回顾解决问题,适度渗透函数思想
在解决问题的过程中,学生积累了几组有联系的计算题,对这些题组进行整体观察,可以发现它们的变化规律。即“单价”“数量”“总价”这三种量中,当其中一种量不变,另外两种量之间的函数关系。
图6是在解决上述问题时形成的板书。

图6
教师引导学生观察上面虚框里的3个乘法算式,让学生说一说有什么发现。
生1:我发现“单价”不变,数量增加,总价也增加。
生2:我发现“单价”不变,数量乘几,总价也乘几。
依据生1的回答,教师在数量关系中的总价与单价处各加上向上的实线箭头。接着教师各添上向下的虚线箭头,请学生说一说这表示什么。同样地,在生2回答后,在题组中进行举例验证,并追问,还可以发现什么规律?通过举例概括一个因数除以一个数(0除外),积也除以相同的数。
针对下面的虚线框,教师追问:为什么不选择单价是“10元/支”的?
生1:因为买的支数要增加,那么单价就要变小。
生2:支数乘2变成了60支,单价除以2变成了4元/支。
最后形成如图7的板书。通过题组,把数量关系看作函数关系,拓展学生对数量关系的理解。这既是上一节课中的思维方式的延续,也为后续学习“归一问题”“归总问题”和“正反比例应用问题”做铺垫。
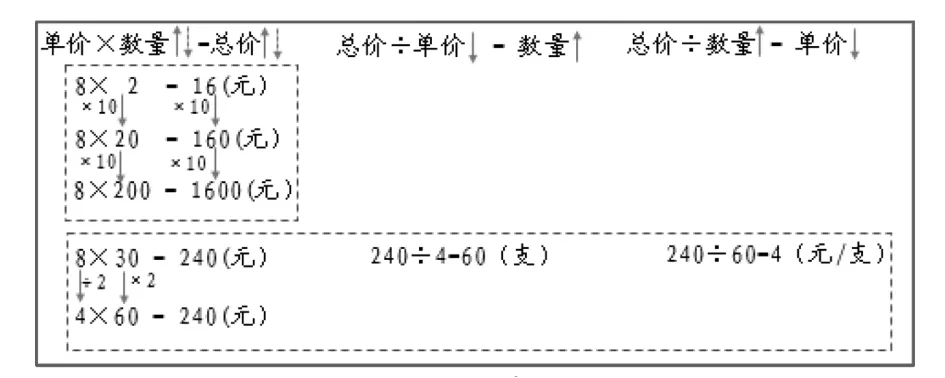
图7
三、边练边思,巩固与应用数量关系解决问题
数量关系在解决问题的过程中概括,然后要回到解决问题的过程中进行巩固,并在不断地应用过程中加深对数量关系的理解,灵活地应用数量关系解决问题,提升学生发现问题、提出问题、分析问题与解决问题的能力。
(一)依据信息,提出问题
在新知学习后,需要安排相应的基础练习,让学生应用新知解决问题,巩固思维。作为常见的数量关系,教师可以编制不同的现实情境,让学生进一步体会数量关系的一般性与现实情境的丰富性。
根据已知信息提出问题并解答。(1)每个篮球80元,老师买了3个,_______________?
(2)买4千克甲鱼共花费了240元,_______________?
(3)学校花240元买字典,每本字典60元,______________?
教师让学生依据已知的信息提出问题,然后列出数量关系,口头回答出算式与结果,并将算式写到与数量关系相对应的板书中。
(二)合理选择,提出合适的数学问题
算用结合是数学学习的基本思路。利用运算解决具体问题,并从中总结出数量关系,是学习的主要形式。结合算式,提出相应的问题,可以更好地促进学生对数量关系结构的把握。
在上面一组练习中,分别用如下3个算式解答:①80×3=240 ②240÷4=60 ③240÷60=4。请学生观察这几个算式之间的联系,选择其中有联系的两个式子,编写一道两步计算的应用问题,并且数量关系要求是本节课新学习的内容。
选择算式编写应用问题,促使学生能够寻找算式之间的关系,赋予“数”以具体的意义,通过交流,发现同样的算式可以有不同的情境,不同的情境在解决问题时又有相同的数量关系。
(三)灵活应用,结合实际解决问题
在实际生活中,商品有零买也有成批买,而成批买会便宜些。因此,教师也可以创设这样的情境,让学生合理地制订购买方案,使所花的钱最少。
某商店的农夫山泉矿泉水有两种买法(如图8),如果买6瓶,需要多少元?如果买36瓶呢?如果买42瓶呢?

图8
解决第2个问题时,需要判断整箱买每瓶的单价是多少元,是否比单独买要便宜一些?当解决第3个问题时,则需要判断42瓶里面有几个18瓶,还余下几瓶?分成两个部分分别求出单价再相加。可以先请学生独立计算,然后反馈讲评。
总之,商品买卖中的数量关系的学习,是学生第一次对多个具体数量关系相同点的抽象概括。在这一个过程中,可以让学生结合具体的例子,体会数量关系中各个量之间的变化关系,渗透函数思想,感受数学的内在魅力。

