基于“深度学习”的初中数学单元复习课教学策略*—以北师大版《三角形的证明》单元复习课为例
广东省佛山市顺德区沙滘初级中学(528315) 黄莹
随着学习研究的深入,深度学习已成为新时代背景下一种重要而有效的学习方式和学习理念,也是落实学科核心素养的有效途径.深度学习是一种主动的、批判性的学习方式,也是实现有意义学习的有效方式.这种学习方式要求学习者进行理解性的学习、批判性的高阶思维、主动的知识建构、有效的知识迁移及真实问题的解决.
一、借用思维导图,完善知识网络
在单元复习课中使用“思维导图”进行复习,可以唤起学生已有经验,将整个单元所学的内容进行串联起来,将概念之间的同、异及内在联系,进行整理,实现知识的迁移和归纳,让学生的思维“可视化”,能达到良好的复习效果.
(一)课前知识点整理环节.在双休日,布置给学生具体的复习要求:一是在复习回忆基础上对知识要点进行归纳整理;二是记录与此相关的问题和提问.这样既使学生学习有了明确的目标导向,体现了不同个体的学习需求,又为教师收集信息提供了机会.如,《三角形的证明》单元复习课前,笔者班上大部分学生都能把这一单元的知识点进行板块化处理:(1)等腰三角形;(2)等边三角形;(3)直角三角形;(4)线段垂直平分线;(5)角平分线.并把本章的所有定理进行列举.
(二)课中思维导图串联知识点.复习课第一个环节就是系统、完善和深化所学内容,从而达到进一步完善优化学生的知识结构.在课前我们已经让学生完成了知识整理,但也只是一些零碎的知识.在本环节我们利用小组合作的形式,用思维导图把我们整理的知识点串联起来.
师:同学们,周末我请大家把《三角形的证明》这单元的知识进行了归纳、整理.现在哪一位同学把自己对这部分知识归类整理的情况给大家展示一下?
设计意图学会对知识进行整理,先由学生自己对该部分知识进行归纳总结,巩固本章所学的内容.在课堂上展示后再通过师生共同评价修正,从而帮助学生建立整体认知框架,完善认知机构.
效果:学生积极展示自己的整理结果,有的同学直接罗列知识点;有的用“框架图”把知识点进行了分类;还有个别同学用彩色的“树状图”把这五个知识点连了起来,学生整理的结果超乎我的想象.
师:第三位同学的“树状图”非常形象生动,把五个知识点串联起来,为什么能用线把这五个知识点连起来?他们之间是否存在关联?
设计意图学会思考知识点之间的联系,建构知识网络,引发学生的深度思考.
生1:等腰三角形和等边三角形可以连,等边三角形是等腰三角形的特殊情况.
师(追问):你能说说它们两者的异同吗?
生1:等腰三角形有的性质,等边三角形都有;等边三角形有的性质,等腰三角形不一定有.如,等边三角形三个角都相等,都等于60°,三条边都相等.
师(追问):很好,我希望你能在你的知识整理中,把这两个知识点连接起来,并在连线上分别写出它们的相同点和不同点.其他连线呢?
……
在老师的追问下,学生通过小组讨论,不断深挖这五个知识点的关联.充分引发学生的深度思考,形成完整的知识网络.
(三)概括提炼数学思想方法.数学思想方法是对数学知识的概括,也是数学知识的本质所在.对数学思想方法进行的提炼,是从方法论角度给学生提供了数学学习的方法.不仅有助于对数学知识的理解和运用,能有效提高数学的学习效率,对提高个体的整体素养也具有重要的现实意义.
二、借用“题组训练”,提升学生知识迁移能力
有了上一个环节的铺垫,学生对本单元的内容已经有了整体的认识,但在实际应用上,如何调用本章的知识解决问题仍有困难.所以我们采用有针对性的“题组训练”来提升学生知识的迁移能力.
(一)基础题组的设置
通过基础题组的复习,旨在对复习内容的基础知识点做一个系统的梳理.根据《课程标准》对《三角形的证明》教学的要求,设置基础题组时要充分考虑到对基础知识掌握情况的查漏补缺.教师共设计了五道基础题,为了减少这一部分解题的时间,五道题目中有两道选择题,两道填空题,一道解答题.
(1)已知一个等腰三角形两边长分别为5,6,则它的周长为( )
A.16 B.17 C.16或17 D.10或12
(2)如图1,在 Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=n,AB=m,则△ABD的面积是( )
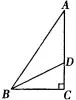
图1
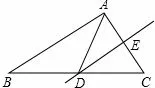
图2
(3)如图2,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是___cm.
(4)如图3,三角形△ABC是等边三角形,BD平分∠ABC,点E在BC延长线上,且CE=1,∠E=30°,则BC=___.
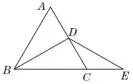
图3
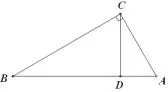
图4
(5)如图4,△ABC中,∠ACB=90°,CD⊥AB,垂足是D,∠B=30°.求证:BD=3AD.
设计意图帮助学生掌握(1)等腰三角形;(2)等边三角形;(3)直角三角形;(4)线段垂直平分线;(5)角平分线这五个知识点,设置了此五道题.
(二)变式题组的设置
变式题组就是通过改变条件或结论而形成的一系列小题构成一个题组的教学方式,通过题组中数学问题的探究和解决,学习巩固知识,解决教学重难点,并通过变式问题的对比,揭示数学问题本质规律,培养学生辩证思维能力,从而达到深度学习的目的.
例1 已知:如图5,△ABC的两条高BE、CD相交于点O,且OB=OC,求证:△ABC是等腰三角形.
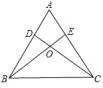
图5

图6
变式1如图6,在△ABC中,AB=AC,∠BAD=∠CAE,点D、E在BC上,试说明△ADE是等腰三角形.
例2已知,如图7,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF.求证:AF为∠BAC的平分线.
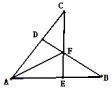
图7
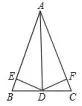
图8
变式2 如图8,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.
设计意图变换问题的非本质要素,突出本质要素,掌握问题的本质不仅可以帮助学生构建知识网络,加深对数学问题本质的认识.进一步提高学生分析、归纳解决问题的能力,学会知识的迁移.
(三)课后题组的设置
学生的水平必定存在差异,我们不可能通过一节复习课就能把学生的整体水平拔高,课后题组的设置是进一步对学生对本单元内容的巩固与提升.练习题分层设置,由易到难,既有对课堂复习的回顾,又有一定的拓展提高.采用中考真题,科学地检测学生对三角形的证明知识的掌握程度和审题、解题能力.
三、数学复习课型的构建过程的思考
数学复习课是教师帮助学生梳理知识结构,形成知识网络,提高数学成绩的重要过程,同时也是提升学生数学素养的重要阶段.有效、实用的教学设计是教师永恒的追求.教师要坚持以学生为本的理念,复习过程中在引导学生寻找知识之间的关联、引发学生的深度思考,提升学生自身的学习能力、知识迁移能力,让学生积极参与复习过程,教师起到穿针引线的作用,也就是课标提出的教师是学习的组织者、引导者和合作者,而不是包办者.只有这样,才能真正实现学生的深度学习.

