融合信息技术与高中数学课程*—探索数学素养培育新途径

安徽省芜湖市第十二中学(241002) 黄太强

探究基于数学核心素养培育的教学已成为当下的趋势.在数学核心素养的指导下,课堂教学更加注重思维与能力的提升.教师如何落实核心素养的培育呢?笔者所在学校建有省内首个数学实验室,配备了先进的信息技术设施.笔者在教学实践中,通过信息技术与课程的整合实践,发现将信息技术融入课堂,可以用不同方式将数学知识的内在规律展现出来.以下结合笔者在教学过程中的实践,谈几点体会.

1、利用信息技术验证数学猜想,培育数学建模素养

数学建模能力是指能够在实际情境中,从数学的视角提出问题,用数学的思想分析问题,用数学的语言表达问题,用数学的知识得到模型,用数学的方法得到结论,验证数学结论与实际问题的相符程度,不断反思和改进模型,最终得到符合实际规律的结果[1].传统教学受教育技术的限制,实践效果并不理想.笔者在信息技术环境下让学生解决一些具有真实背景的、开放度、综合性较高的问题,尝试着把培养学生解决问题的实践能力和创新能力在课堂教学中得以落实.

例如,在人教版高中数学必修四《三角函数模型的简单应用》后,设置了如下问题：

制作一个排烟筒的弯头部分(图1),选用的矩形铁片应满足怎样的尺寸?请你在矩形铁片上画出最合理的裁剪线.

图1 排烟筒弯头

图2 切开火腿肠包装纸

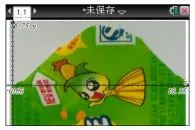
图3 导入图形计算器

课前准备：切去火腿肠两头,形成一个圆柱体,将该圆柱体按约45°斜切成两段,拼成一个排烟筒弯头的模型.用小刀按图2将其中一段火腿肠包装纸切开,平铺在一张纸上.最后将展开图拍照后形成电子图片,导入TI Nspire图形计算器的坐标系中(图3),利用无线导航系统(TI Nspire Navigator)发送到学生的图形计算器上.

课内交流：

师：根据你的观察,它像哪一类函数的图象?

设计意图引导学生聚焦于图象的范围、对称性、单调性等特征.通过小组讨论,猜想截面椭圆的展开曲线可能是抛物线或者是正弦型函数y=Asin(ωx+φ)+k图象.

师：如何对此结论进行判断?

生：先利用图形计算器对图象进行函数拟合,然后再设法求出函数表达式.

师：请大家完成下面的操作：

(1)在曲线上选择一些点,测量各点的坐标,形成电子表格；

(2)选用二次函数模型以及正弦型函数模型进行回归分析,并比较结果.

教师利用无线导航系统将其中一个小组讨论的结果(图4)投影至大屏幕：

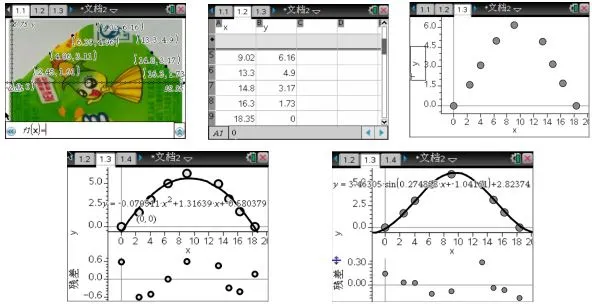
图4 学生小组讨论结果

对于上述问题,学生能够从数学的视角表述问题,提出猜想,在信息技术的帮助下,完成数据的采集、函数的拟合以及残差分析,进而培养了学生的数学建模能力.

2、利用信息技术探究命题变式,培育逻辑推理素养

逻辑推理是指从一些事实和命题出发,依据逻辑规则推出一个命题的思维过程.而“变式教学”通过层层递进的设问,可以培养学生的思维能力,孕育提高逻辑推理素养[1].传统教学中,由于研究手段的匮乏,“变式教学”容易“启而不发”.信息技术是观察数学现象的望远镜.笔者发现,学生使用信息技术做“数学实验”,进行观察、分析、探索和归纳,可以体验数学、理解数学.

在人教版高中数学必修二《圆的方程》中,课本设置了以下问题：

已知点M与点O(0,0),A(3,0)的距离的比为,求点M的轨迹方程.

已知点P(2,0),Q(8,0),点M与点P的距离是它与点Q的距离的,求点M的轨迹方程.

我们可以配置一个“数学实验”：

已知点M与两个定点M1,M2的距离的比是一个正数m,用《几何画板》探究点M的轨迹(图5).

图5 几何画板

该“数学实验”把前面两个问题一般化,加强了教材前后内容的联系.在信息技术支持下,学生通过动手操作观察,当点M移动时,距离的比保持不变,猜想点M的轨迹是圆(阿波罗尼兹圆),然后用“坐标法”给出代数证明.

在探究点的轨迹、求曲线方程的过程中,有了信息技术的支持,彻底改变了传统教学中动点不动的缺憾,让“动点”真的动了起来,使数学思维形象化,学生能集中精力反思、推理进而解决问题.

3、利用信息技术动态生成教学内容,培育数据分析素养

教学中利用的信息技术,最容易想到的就是PPT.但PPT只能按照教师预先的设计一步一步展示教学内容,对于课堂的动态生成结果往往无法表现.Excel自身具有强大的函数功能及利用数据绘制图表的功能,从而能够利用课堂上实时生成的数据,动态生成教学内容,帮助学生从数据中提取有用的信息,利用图表展示数据,构建模型分析数据,解释数据蕴含的结论,从而加强学生的数据分析能力.

笔者在人教版高中数学必修三《随机事件的概率》的教学中,为让学生体会随机事件发生的随机性和规律性,选取了布丰投针实验,下面是该实验的教学片段：

在画有等距平行线的纸上,随机的抛掷一根小木棒,研究木棒与平行线有交点的概率.学生4人一组,共15组,每组抛掷20次.

汇总实验结果：小组成员将数据输入到计算机的Excel中,自动产生各组频率并绘制出相应的折线图(图6).

图6 频率折线图

师：是否能发现规律,帮助我们估计事件发生的概率?

设计意图学生的亲身体验,更有利于概念的形成.对于各组频率统计表,学生也可以从中观察出一定的规律,但是这一规律不够明显.在此处设置思考问题,引发学生进一步思考,培养学生分析数据的能力.

生：教材中出现的篮球运动员三分球命中率估计,就是一种累积数据的想法.而累积数据就相当于大量重复同一实验.故这里可以利用Excel的计算功能,计算出累积各组数据之后的频率,并绘制出折线图.

学生绘制出图7,从数和形两个角度观察.学生都能得出累积数据的频率体现出规律性这一结论.

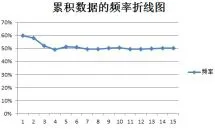
图7 累积数据频率折线图

设计意图这一部分是本节内容的难点,需要把对数据、图表的直观印象转化为抽象的概率定义.之所以可以用大量重复试验的频率来估计概率,是因为在数、图中累积数据的频率体现出了一定的“稳定性”,即规律性.使得我们能够从图表中判断出事件概率的范围.

在Excel的使用过程中,笔者往往采取的是先对要分析的内容进行讲解,然后让学生制定操作步骤,思考如何通过相应数据来反映其想说明的问题.提高了学生数据分析的能力,同时也使得课堂充满了更多的探究氛围.

融合不是混合,应用信息技术是教学手段而不是最终目的.有了信息技术,与“体力劳动”相关的内容(如繁杂的计算)减少,与“脑力劳动”相关的内容(如算法设计、模型选择)增加,这样就可以让学生有更多的时间用于理解数学的本质,从而更有效地培养学生的数学素养[2].努力构建基于“融合”观下的教学内容和教学设计的模式,以适应培育数学核心素养需求,才是将信息技术引入课堂的真正意义.