利用TI图形计算器辅助不等式教学

广东省广州市从化区第二中学(510900) 杜东仪

不等式部分的教学非常强调不等式及其证明的几何意义与背景,以加深学生对这些不等式的数学本质的理解,提高学生的逻辑思维能力和分析解决问题的能力.但由于2011版的课程标准把不等式的放到了整个高中数学必修模块的最后一部分且对证明不等式的要求有所降低,让大部分教师在不等式教学中有所忽视,造成学生答题不严密、不规范,甚至答案正确但解题思路错误的情况出现.而2017版课程标准将不等关系放到了第一册的预备知识中,足见它的基础性意义及重要性.

在作业批改、学生分层辅导中,我发现相当大一部分学生在解答不等式与不等关系的题目时并没有真正理解好不等关系的实际意义,往往仅仅是对教师教给方法的机械重复、简单默写.为了真实了解教学效果,本人以问卷调查等形式,针对学生在作业中存在的问题进行调查研究,比如将一道不等式题的两种不同解法(其中一种正确一种错误,但答案安全相同)呈现给学生,并让学生分辨对错.通过调查研究,我发现学生在不等式方面普遍存在以下的几个问题：

问题一将两个互相制约变量的取值范围分离,导致不等式组范围扩大

例1设函数f(x)=ax2+bx,且1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.

学生A(正解)：因为f(x)=ax2+bx,所以f(-1)=a-b,f(1)=a+b,f(-2)=4a-2b,又因为1≤f(-1)≤2,2≤f(1)≤ 4,所以因为设4a-2b=m(a-b)+n(a+b)=(m+n)a+(n-m)b,所以解得m=3,n=1,所以①×3+②得：5≤4a-2b≤10,所以f(-2)的取值范围为[5,10].

学生B(错解)：因为f(x)=ax2+bx,所以f(-1)=a-b,f(1)=a+b,f(-2)=4a-2b,又因为1≤f(-1)≤2,2≤f(1)≤ 4,所以所以①+②得：3≤2a≤6③,所以①×2+③得：5≤4a-2b≤10,所以f(-2)的取值范围为[5,10].

两个学生都运用了不等式同向相加的性质进行运算,表面看起来好像没什么区别.但仔细观察,我们可以发现学生B在解答过程中出现了一个“3≤2a≤6”的式子,问题就出在这里了.与是两个互相制约的变量,a的取值会受到b的影响,当我们单独求出a或b的范围时,实际上已经是扩大了不等式组的取值范围,导致解答错误.学生A用待定系数的方法却不一样,他始终坚持将a+b与a-b作为整体来运算,利用同向相加的过程中,等号成立的条件始终保持一致,所以范围并没有扩大,因此解答正确.

问题一中学生出错的主要原因是对a与b相互制约的性质认识不清,a与b单独求范围为什么会导致范围扩大的原因不明确.很多老师在讲解时并没有让学生真正清楚认识到范围扩大的原因.其实,这部分如果引入线性规划的知识进行说明就会一目了然.对此,我设计了一系列的探索过程：

1.根据同学A与B解答中出现的不等式组画出不同的可行域和目标函数.

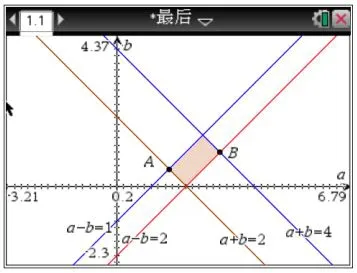
图1

图2

学生通过画图,亲身感受可行域的变化情况,从而体会同学B的解答过程中单独求出a或b的取值范围时,实际上是将不等式组表示的范围扩大了.

2.引导学生思考：为什么平面区域发生了变化,但4a-2b的取值范围却仍然一样呢?(如图3)

利用TI图形计算器的绘图功能,我们将两个不等式组所表示的平面区域放在同一个直角坐标系中,让学生直观感受到可行域的扩大,但是由于取得最大最小值的点却没有发生改变,导致两种解法出现了一样的结果.但同时,学生产生了一个疑问：即使可行域扩大了,是不是不会影响到最终结果呢?

3.设置疑问：若目标函数改为“f(2)=4a+2b”,同学A与B的解题方法还能得出一样的结果吗?(如图3)

图3

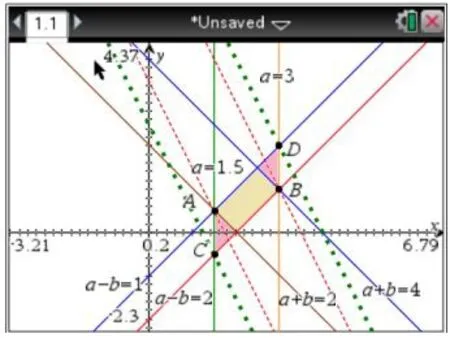
图4

在TI图形计算器中,我们通过移动目标函数,得出原题中是在A,B两点处取得最值,但扩大后的平面区域却是在C,D两点处取得最值,显然目标函数的取值范围也跟着扩大了.TI图形计算器的使用,使学生直观感受可行域的扩大对“f(2)=4a+2b”的取值范围的影响,从而得出结论：若将两个互相制约变量的取值范围分离,会导致不等式组的范围扩大而出错.

问题二放缩法在不等式求解中的应用问题

在绝对值不等式的证明题中,我们可以利用不等号的传递性进行证明,也就是我们常说的放缩法.比如,我们要证明“|x-1|+|x+2|＞2恒成立”,我们可以利用绝对值的三角不等式“|x-1|+|x+2|≥|(x-1)-(x+2)|=3”和“3＞2”得证.由于方法简单快捷,一般学生都掌握得比较好,同时也有较多的学生会应用到绝对值不等式的求解中,但不等式的求解必须做到“同解变形”,因此导致出错.

例2解不等式|x-1|+|x+3|≥6.

解因为|x-1|+|x+3|≥|(x-1)+(x+3)|=|2x+2|,又因为|x-1|+|x+3|≥6,所以|2x+2|≥6,解得x≤-4或x≥2,所以不等式的解集为(-∞,-4]∪[2,+∞)

问题二中学生出错的主要原因是在不等式求解中运用了放缩法,放缩法的主要问题在于有可能将范围扩大或缩小了,而不等式的求解要求的是同解变形,范围的扩大或缩小都可能导致解集发生改变.传统的教学中,教师的讲解的直观性不强,而且不能很好地说清楚不能简单放缩的原因.针对以上问题,我做了一些改进：

1.在TI图形计算器中绘制函数y=|x-1|+|x+3|,y=|2x+2|,y=6的图象.(如图5)

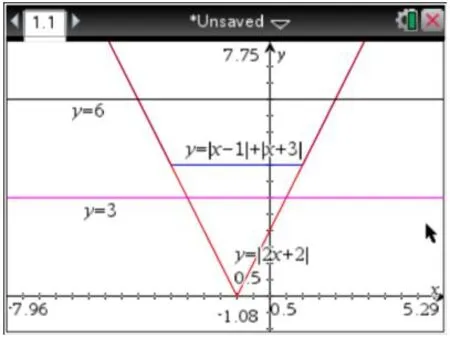
图5

2.观察并总结函数y=|x-1|+|x+3|与y=|2x+2|的图象在什么位置重合,什么位置不重合.

结论在区间(-∞,-3]和[1,+∞)图象重合；在区间(-3,1)不重合.

3.观察函数图象思考下列问题：

(1)不等式|x-1|+|x+3|≥6和|2x+2|≥6的解集是否相同?

(2)不等式|x-1|+|x+3|≥3和|2x+2|≥3的解集是否相同?

结论当y=6时,由于交点在图象重合部分,因此|x-1|+|x+3|≥6和|2x+2|≥6的解集相同；但当y=3时,由于交点在图象不重合部分,因此|x-1|+|x+3|≥3和|2x+2|≥3的解集不相同.

通过设问的形式层层深入,并利用TI图形计算器的绘图功能直观展示,使学生对放缩法的理解理深一层.

在高中的数学教学中,不等式是学生学习的一个难点,主要用于不等关系与他们的恒等变换的基础相背,导致在理解中无法直接转换.因此,我们要注重培养他们不等关系的意识.在以后的学习过程中慢慢的认识不等式,理解不等关系.这就需要我们老师在高一教学之初就要有远瞻的目光,不光要注意到现今学段的内容,更要对日后的学习有所铺垫.TI图形计算器辅助不等式教学的效果非常明显,不但增强了学生学习不等式的信心,还使学生的直观想象能力得到了提升.