一种结构健康监测与载荷监控并行的方法研究

侯乔乔，张清勇，吝继锋

(中国飞机强度研究所，陕西 西安 710065)

1 引 言

在以往的疲劳试验中，结构健康监测与载荷监控工作是基于两套测量系统完成的。一般流程是，在试验完成一定的起落数后，通过探伤检测仪对机体结构尤其是易损伤部位进行全面检测。目前应用比较广泛的结构健康监测手段有人眼目视检查，超声波探伤[1-5]，应力波探伤，磁粉探伤[6-7]，工业射线、CT探伤[8]等，而载荷监控则是基于应变测量系统及其数据来完成的。即结构健康监测与载荷监控过程相互独立。基于应变数据的结构健康监测与载荷监控并行的方法，可以同时实时对结构健康进行监测和对载荷进行监控，这样可以节省停止试验进行检查的时间，或者将停机检查的频次降低。

疲劳裂纹检查是全机疲劳试验中一项非常重要的工作，同时也是一项耗时费力的工作。通常在试验进行一定周期后，由检测人员携带测量设备进入机体各个部位进行检查。基于应变数据的监测方法，可在飞机制造过程中，将应变计一次性布置于典型位置，做好防护。然后根据飞行载荷谱、飞行参数等数据，对采集到的应变测量数据进行分析，进而建立事件(裂纹产生与扩展)识别模型。最后，在飞机飞行或者进行疲劳试验的过程中，在线实时监测应变数据，根据模型做出判断。

2 理论基础

基于应变数据的结构健康监测与载荷监控是依据力学以及控制理论的原理提出的。将飞机机体看作一种结构，对应一定的载荷谱与飞行参数(本质上也是载荷谱)，必然对应一定的应变响应数据。进一步简化，就是建立“结构、载荷、响应”三者相互关系的模型，通过监测载荷与响应，从而判断结构的微小变化(裂纹)。如图1所示，f(t)为输入载荷谱，X(t)为应变响应数据，一般为向量。

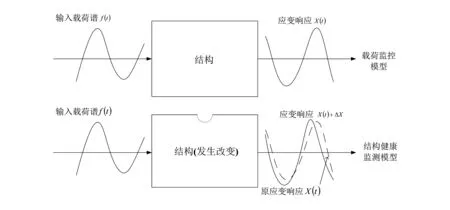
图1 结构、载荷、应变三者关系简图

当机体产生裂纹，在相同载荷作用下，应变响应必然相应地发生改变，改变的程度取决于工程经验决定的对裂纹产生位置的预判能力。如果对裂纹产生的位置预判越接近，则得到的应变响应变化量越明显。

3 结构健康监测模型

如何定义合适的结构变化与应变数据之间模型，以及数据模型的特征提取方法，是达到工程应用层面的关键所在。下面以疲劳试验中的载荷、应变数据为例，来说明数据模型的建立情况。通常情况下，载荷谱是以大周期循环的方式加载的，即每过一个循环周期，上一个周期中的载荷状态将复现出来。载荷状态是指载荷在机体机构上的分布状态，理论上由一个与时间相关的二维曲面函数Z=f(x,y,t)表达。但为了方便处理，可将f离散化为向量形式，并且忽略动态特性(与时间无关)，如式(1)所示。

(1)

上式中，f表示载荷向量，分量表示载荷向量在离散化节点上的作用分量；xf表示载荷位置向量的x坐标分量；yf表示y坐标向量；Tfx表示对x坐标轴的矩向量；Tfy表示对y坐标轴的矩向量。根据载荷分布的形式，构造出的以上5个向量，基本上包含了分布式载荷谱在某一状态下的主要信息，对应不同时刻的载荷谱，则构成了一个向量序列。与此同时，对应于载荷谱的一个状态，产生一个应变响应状态，其数据结构仍然可以用一个向量表示，如式(2)所示。

(2)

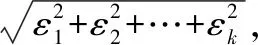
(3)

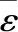
(4)

式(4)中的每一个分量为归一化向量的余弦分量，其取值在[0,1]之间变化。显然，裂纹产生并扩大到一定程度后，传力路径发生改变，附近的应变计εi所对应的余弦分量必然跟着发生改变。如果改变超出了误差的波动范围，则可判定为附近的结构发生了改变。

4 载荷监控模型

载荷计算模型采用成熟的多元线性模型。按照结构动力学的理论，机体、载荷、应变可以抽象简化为结构、激励、响应，标定过程相当于寻找从激励到响应的逆向传递函数。如图2所示。

图2 结构、激励、响应示意图

作用于机体的激励即载荷F(x,y,z,t)，理论上是一个在空间与时间连续的三维向量场函数，响应即应变ε(x,y,z,t)为场函数。为了工程计算得以实现，需要做降维处理，通常的做法是将常激励函数的作用转换为弯矩、剪力、扭矩(分别以M,Q,T表示)折算到机体的某一测量剖面。同时，对应变也进行降维处理，在主要传力通道选取数量有限的测点，场函数ε(x,y,z,t)降维为向量(ε1,ε2,…,εn)。

至此，图2所示的模型经过降维处理以后，载荷与飞机以及应变响应之间的关系变成简单的线性关系。数学模型如下：

M=a1ε1+a2ε2+…+anεn
Q=b1ε1+b2ε2+…+bmεm
T=c1ε1+c2ε2+…+ckεk

(5)

式中，M为折算到某站位的弯矩载荷；Q为折算到某站位的剪力载荷；T为折算到某站位的扭矩载荷；a,b,c为模型系数；ε为应变变量；n,m,k为下标，代表引入模型的应变变量个数。

理论上，弯剪扭载荷方程引入的应变变量可以相同，也可以不同。引入哪些变量，需要根据标定数据进行筛选。称标定试验时的每一组载荷与应变响应数据为一组样本，样本数量必须大于n,m,k中的最大者，才能对式(5)中的每个方程进行回归。回归以后得到方程的系数，最后，根据实测应变响应值代入方程计算未知载荷。

5 工程算例

5.1 结构健康监测工程算例

以某型飞机静力试验中结构发生不可恢复性改变的试验数据为例，来检验上述方法的可行性。在对某型飞机静力试验数据进行分析时发现，按照式(3)所定义的载荷向量“结构特征”没有变化，但是应变向量数据的“结构特征”即某一个余弦分量值发生了明显的改变，由此判断是结构状态发生了改变。原始数据如图3所示。

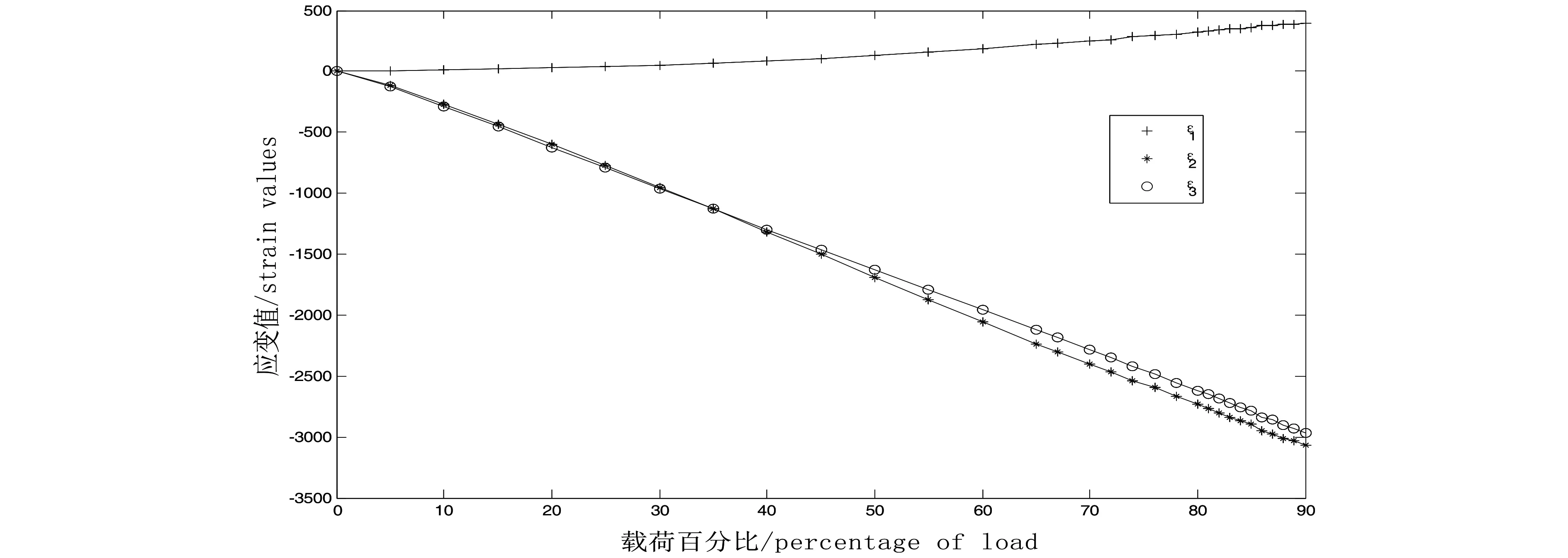
图3 构成应变向量的原始数据

最后通过现场排查，确实发现对应于余弦分量改变的应变计附近的机体发生了不可恢复性改变。试验中，载荷从0%逐级加载到90%水平值，构造一个2维的载荷向量和一个3维应变向量，显然载荷向量的状态在0-90%整个加载过程中没有改变，归一化的载荷向量如下：

(6)

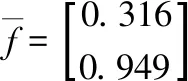
(7)

在40%载荷状态下的归一化应变向量为：

(8)

90%载荷状态下的归一化应变向量为：

(9)

对比两种载荷水平下归一化的应变向量发现，分量1对应的余弦分量发生了较大的变化，而实际上正是应变计ε1附近发生了不可恢复性结构变化，这说明此方法在工程上具有可操作性。

5.2 载荷监控工程算例

以下是某型机全机落震试验中载荷监控的测量结果，数据显示实测结果与理论计算结果吻合得比较好(如图4所示)。

图4 某型机落震试验典型测量剖面载荷历程

6 结 论

从试验结果来看，结构健康检测与载荷监控共用测量系统，互不影响结果与计算精度，证明二者可以基于同一套测量系统，同一组应变数据来并行完成。此方法使得应变测量、结构健康检测与载荷监控三项任务的硬件部分合为一体，可以大幅度减少工作量，降低试验成本。