不等长叠加钢板的弯曲变形计算
吴 晓
(湖南文理学院 机械工程学院,湖南 常德 415000)
1 引 言
叠加梁结构在机械、土木工程中得到广泛应用,例如车辆工程中的悬架钢板弹簧、土木工程中的钢混凝土梁等。叠加钢板弹簧是车辆悬架系统的重要组成部件,叠加钢板弹簧弯曲问题可以归结为悬臂梁的弯曲问题。文献[1]研究了汽车钢板弹簧主片结构的组合优化设计。文献[2]采用“共同曲率”假设研究了叠加钢板弹簧弯曲问题。但是利用文献[2]方法研究叠加钢板弹簧弯曲问题,存在3个缺陷:集中载荷作用下叠加钢板层间压力为零的缺陷,均布载荷作用下叠加钢板层间压力为均布压力的缺陷,外载荷作用下上下层钢板弯曲挠度相等的缺陷。
文献[3-4]认为,剪切变形可以改变集中载荷作用下叠加梁层间压力为零的情况,采用“共同曲率”假设研究了叠加梁的弯曲问题。文献[5-6]在文献[3-4]的基础上,研究了叠加梁的内力计算。文献[7]采用弹性理论,证明集中载荷作用下叠加梁层间压力不为零,且呈曲线分布。众所周知,对于细长梁的弯曲问题,剪切变形的影响是可以忽略不计的,而不等长叠加钢板弹簧都属于细长梁,因此剪切变形对外载荷作用下叠加梁层间压力的影响是可以忽略不计的。
基于上述原因,本文采用“共同曲率中心”方法重新研究了不等长叠加钢板弹簧的弯曲变形计算问题。
2 不等长叠加钢板弹簧弯曲
对于图1所示不等长叠加钢板弹簧,文献[2]采用“共同曲率”假设研究不等长叠加钢板弹簧弯曲会导致:集中载荷作用下叠加钢板层间压力为零、均布载荷作用下叠加钢板层间压力为均布压力、外载荷作用下叠加梁段部分上下钢板弯曲挠度相等的缺陷。

图1 不等长叠加钢板弹簧
事实上,图1所示叠加钢板弹簧弯曲时,仅有共同的“曲率中心”,因此下式成立:
M(x)=M1(x)+M2(x)
(1)
(2)
(3)

由式(1)、式(2)和式(3)可得:
hM12-(Mh+D1+D2)M1+D1M=0
(4)
由式(4)可以求得上层钢板截面弯矩为:
(5)
把式(5)代入式(1)中,可求得下层钢板截面弯矩为:
(6)
上下钢板的弯曲微分方程分别为:
(7)
(8)


(9)
把式(5)代入式(7)中,可得0≤x≤l1时弯曲微分方程为:

(10)
对式(10)积分可得0≤x≤l1时转角方程为:
(11)
对式(11)积分可得0≤x≤l1时挠曲线表达式为:

(12)
把式(6)代入式(8)中,可得0≤x≤l2时弯曲微分方程为:
(13)
对式(13)积分得到0≤x≤l2时转角方程为:
(14)
对式(14)积分得到0≤x≤l2时挠曲线表达式:
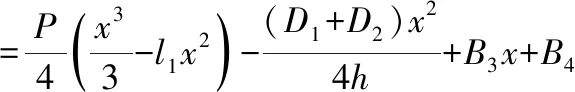
(15)
叠加钢板弹簧上下钢板的边界条件分别为:
(16)
(17)
利用以上有关各式可以确定:


(18)
由式(2)、式(3)可以求得不等长叠加钢板弹簧上下钢板的应力计算公式分别为:
(19)
3 算例分析
以文献[2]讨论的某两片钢板组成的不等长叠加钢板弹簧为例,上钢板厚度h1=12mm,长度一半l1=700mm;下钢板厚度h2=10mm,长度一半l2=500mm。上下钢板宽度均为b=20mm,弹性模量E=200GPa,集中载荷P=200N。
把钢板弹簧材料参数代入式(9)中,可得不等长叠加钢板弹簧层间压力曲线,如图2所示( 0≤x≤l2)。
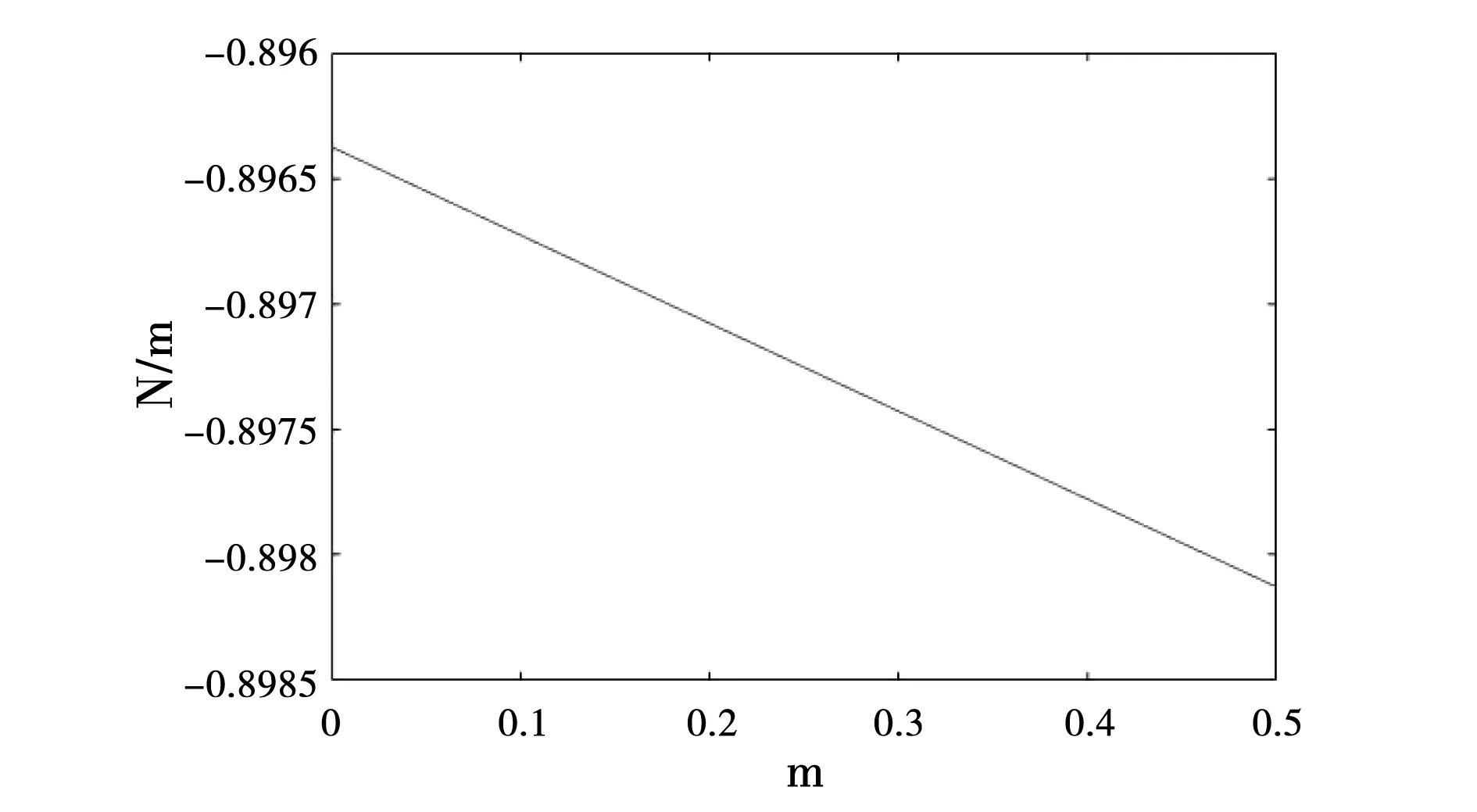
图2 不等长叠加钢板弹簧层间压力
把钢板弹簧材料参数分别代入式(12)、式(15)中,可得x=l2处,不等长叠加钢板弹簧上下层钢板弹簧的挠度分别为w1=-14.68mm,w2=-14.64mm。
再把钢板弹簧材料参数分别代入式(12)中,可得x=l1处,不等长叠加钢板弹簧上层钢板弹簧自由端的挠度为w1=-25.17mm。
而文献[2]采用材料力学理论给出的x=l1处,不等长叠加钢板弹簧上层钢板弹簧的挠度为w1=-25.49mm。
对图2所示曲线进行分析可知,集中载荷作用下,不等长叠加钢板弹簧上、下层钢板弹簧层间压力曲线近似为直线,这一点与文献[7] 吻合。在固定端绝对压力值最大,自由端绝对压力值最小。由于最大绝对压力值层间压力与最小绝对压力值相差较小,因此在集中载荷作用下,叠加钢板弹簧上、下层钢板弹簧层间压力可近似为均布载荷。不等长叠加钢板弹簧在集中载荷作用下,如果把文献[2]采用“共同曲率”假设给出的挠曲线表达式代入式(9)中,可知叠加钢板弹簧上、下层钢板弹簧层间压力为零。不等长叠加钢板弹簧在均布载荷作用下,如果把文献[2]采用“共同曲率”假设给出的挠曲线表达式代入式(9)中,可知叠加钢板弹簧上、下层钢板弹簧层间压力为均布压力,这显然不符合文献[7]给出的弹性理论。
文献[2]采用“共同曲率”假设给出的叠加钢板弹簧上下层钢板弯曲挠度是相同的。 而本文方法给出x=l2处不等长叠加钢板弹簧上下层钢板弹簧的挠度分别为w1=-14.68mm,w2=-14.64mm ,所以叠加钢板弹簧在集中载荷作用下,上下层钢板弯曲挠度是不相同的。造成以上缺陷的原因是,叠加钢板的弯曲是一个非线性问题,仅存在共同“曲率中心”,文献[2-6] 采用“共同曲率”假设研究叠加梁的弯曲问题,则是把非线性问题转化为线性问题。这就是产生“集中载荷作用下叠加钢板层间压力为零的缺陷,均布载荷作用下叠加钢板层间压力为均布压力的缺陷,外载荷作用下上下层钢板弯曲挠度相同的缺陷”的原因。
本文采用共同“曲率中心”方法给出x=l1处不等长叠加钢板弹簧上层钢板弹簧自由端的挠度为w1=-25.17mm,文献[2]采用“共同曲率”假设给出的x=l1处不等长叠加钢板弹簧上层钢板弹簧自由端的挠度为w1=-25.49mm,两种方法计算结果相差不大,实际工程设计都可接受。
4 结 论
(1)产生“集中载荷作用下叠加钢板层间压力为零的缺陷,均布载荷作用下叠加钢板层间压力为均布压力的缺陷,外载荷作用下上下层钢板弯曲挠度相同的缺陷”的原因是:叠加钢板的弯曲是一个非线性问题,仅存在共同“曲率中心”,有关文献采用“共同曲率”假设研究叠加梁的弯曲问题,则是把非线性问题转化为线性问题。
(2)采用共同“曲率中心”方法计算的不等长叠加钢板弹簧上层钢板弹簧自由端的挠度与采用“共同曲率”假设计算的不等长叠加钢板弹簧上层钢板弹簧自由端的挠度相差不大,实际工程设计都可接受。

