航空发动机鲁棒回路成形控制方法研究

王霖萱

(贵州大学，贵州 贵阳 550025)

1 引 言

随着控制理论的发展，传统的鲁棒控制理论广泛应用于实际工程系统中，但是这样的系统在一定程度上忽略了系统的性能鲁棒性，尤其在对输出响应有严格时域指标要求的情况下，可能达不到要求。

为了克服这个缺点，Mcfarlane和Glover[1]结合鲁棒控制理论与回路成形思想，提出了H∞回路成形的算法。该方法通过权函数的选择改善开环传递函数的奇异值频率特性，从而实现系统的闭环性能要求，并利用对规范化互质因式摄动系统的鲁棒镇定分析，得到具有鲁棒稳定性的控制器。相对于其他鲁棒控制方法，特别是传统的H∞混合灵敏度方法，H∞回路成形方法因其能同时满足控制系统的鲁棒稳定性要求和性能要求，且迭代次数少，吸引了大量学者的关注。之后，Glover分析了回路成形方法中的稳定边界指标εmax与SISO系统的相角裕度、幅值裕度之间的关系[2]，使稳定边界指标的意义更加工程化。Bernstein和Haddad[3]提出H2/H∞混合控制，结合系统的最优性能和鲁棒性，通过求解最优控制器使系统获得较好的动态特性。

本文为了进一步提高控制系统的整体性能，引入二自由度控制思想，并将其与鲁棒回路成形H∞LSDP控制算法相结合[4]，通过改进控制器设计结构，优化控制算法，降低鲁棒控制的保守性，以满足航空发动机控制系统高性能要求。

2 H∞LSDP的系统设计方法

H∞LSDP是在闭环系统中引入前置和后置补偿对象的方法，对开环奇异值进行整形，以使最终的闭环系统满足期望的性能指标。在低频段，使系统开环传递函数的奇异值尽可能大，以保证系统良好的输入跟踪能力和抗干扰能力；在高频段，使系统开环奇异值尽可能小，以增强抑制噪声的能力。而后，对“被整形”对象实施鲁棒镇定。本文的设计方法是在回路成形方法基础上进行分析的。

H∞LSDP控制结构[4]如图1所示。控制器的结构采用前馈加反馈的方法。其中，控制器的反馈部分用来满足鲁棒稳定性和抑制扰动的需求，除了只引入一个前置补偿权函数W外，所采用的方式与传统的回路整形设计方法类似。Tref称为系统的参考模型，在控制中额外引入前置滤波器，以强制闭环系统的输出响应跟踪参考模型Tref的响应。ρ是一标量参数，在优化过程中，可以通过增大其取值以获得更好的模型匹配性能，但是这样做的同时会降低系统的鲁棒性。

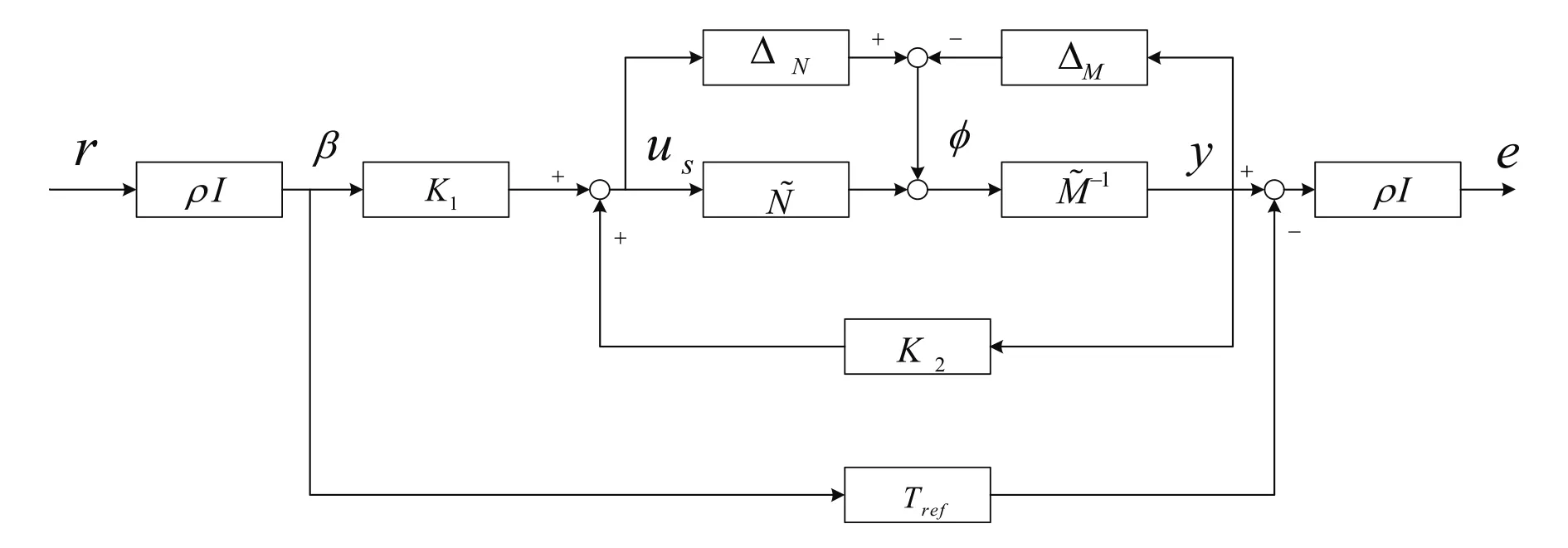
图1 H∞LSDP控制结构

根据结构图，可得系统的分块矩阵传递函数为：

为把该设计问题转化为标准的控制问题，可以定义如下的广义被控对象：

综上所述，H∞LSDP控制器设计步骤为：

(1)对控制结构进行优化，即对输入输出进行排序，尽可能将对象对角化。这样做的目的是为了简化前置和后置补偿器的设计。

(2)根据传统的回路成形方法，选择合适的前置补偿器W1和后置补偿器W2，得到期望的开环奇异值曲线。之后计算鲁棒稳定边界，保证系统具有合适的不确定摄动。

(3)选择期望的从控制指令到被控输出的闭环传递函数Tref。Tref为对角矩阵，以使系统尽可能解耦。

(4)把标量参数ρ设置为大于1的较小值，通常在1～3之间就能满足要求。

(5)对于被整形对象Gs=WpGW1、期望的响应Tref以及标量参数ρ，求解标准H∞优化问题，得到控制器K。

(6)对所设计的控制器进行仿真，如果仿真效果欠佳，重新调整ρ、Tref的值以获得满意的控制效果。

3 控制器设计

以某型涡扇发动机[5]为例，设计H∞LSDP控制器。首先选取设计工况点，以H=11km，Ma=1.5，相对转速为96%的飞行条件为例，建立发动机的三变量归一化小偏离状态空间模型：

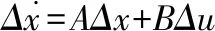
其中，x=[NLNH]T，y=[Tt4PRSMF]T，u=[WFBA8VGV]T。

首先需要对航空发动机进行奇异值分析，分析结果如图2所示。

图2 原对象的奇异值

从图2可以看出，原对象低频段的奇异值基本接近1，系统对输入的跟踪能力很差，因此要对控制对象进行整形，需要一个额外的低频增益，以得到良好的稳态跟踪能力和扰动抑制能力。基于此，前置补偿器的权函数选为积分器，即WP=I3/s；原系统的高频部分的响应衰减速率达到了20dB/十倍频程，基本可以达到抑制高频干扰的能力。因此，后置补偿器的权函数可以简单地选为W2=I3。

被整形对象Gs=W2GW1，其中W1=WpWa。利用与Wp串联在一起的常值权函数Wa，将奇异值排列在期望的带宽范围内。Wa是一个有效的常值解耦器。整形后的奇异值如图3所示。

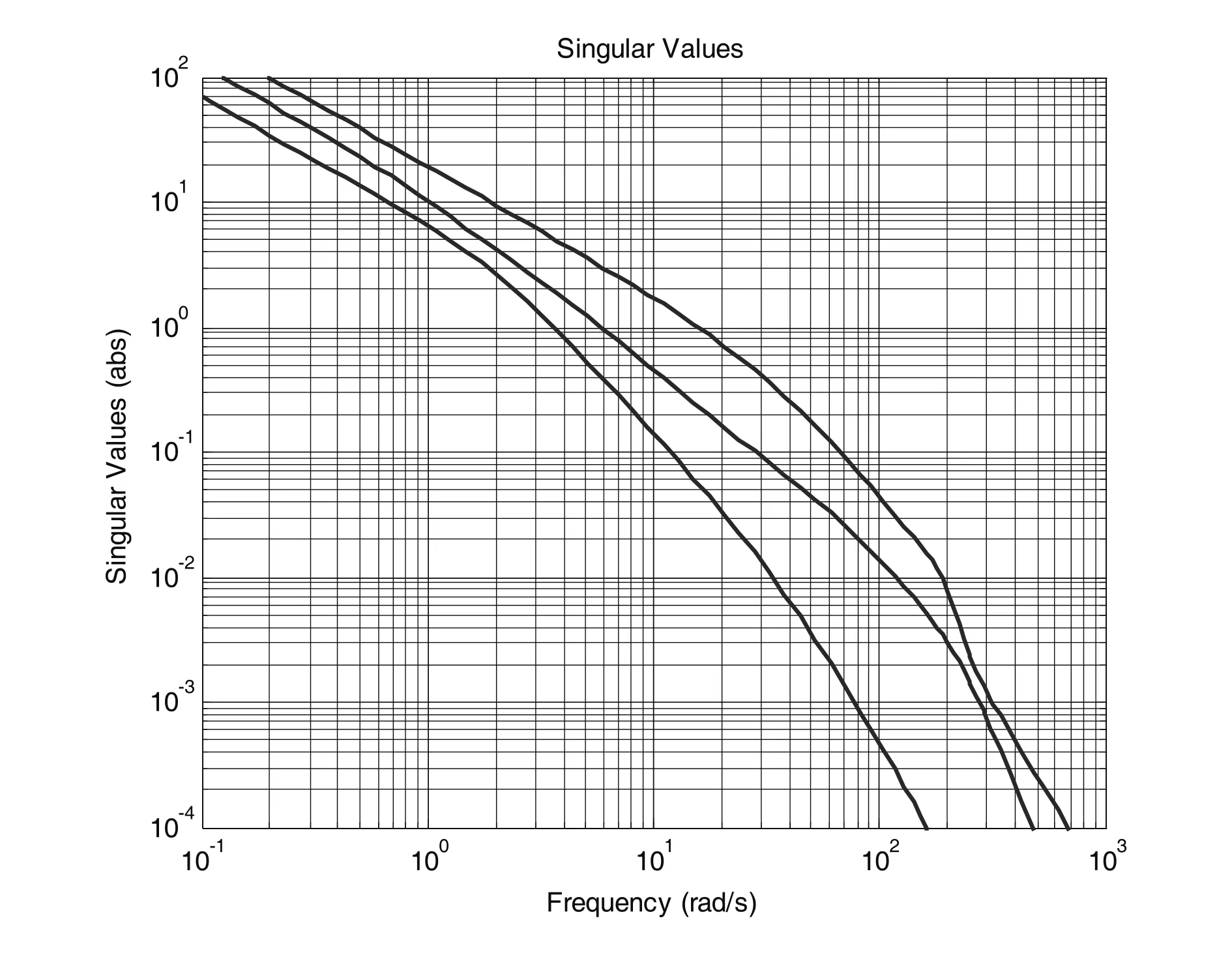
图3 整形后的奇异值

按照步骤(2)，计算系统的鲁棒稳定边界，具体如下：

1.4142<γ<2.8814

选择参考模型Tref，使其能反映发动机的闭环系统响应特性。

选择参数ρ=1，利用常规的H∞方法求解控制器K。之后对设计出的控制器的性能进行仿真验证，不断调整上述变量的值，以获得最佳控制效果。最终选定ρ=1.5，采用γ迭代，得到γ=2的次优控制器。

4 仿真算例

对上述H∞LSDP解耦控制器进行数字仿真。

(1)系统的解耦能力以及跟踪参考指令能力，具体如图4所示。图中给出了线性被控对象模型参考输入的阶跃响应。由图可知，系统解耦很好，只有不到10%的相互作用，且系统的响应时间<1s，能很好地跟踪给定的参考输入。

(2)对结构不确定性的鲁棒性：利用该控制器对附近工作点的模型进行控制，选取其中的一个工作点H=11km，Ma=1.2，将此控制器应用于该模型，得到的控制结果如图5所示。

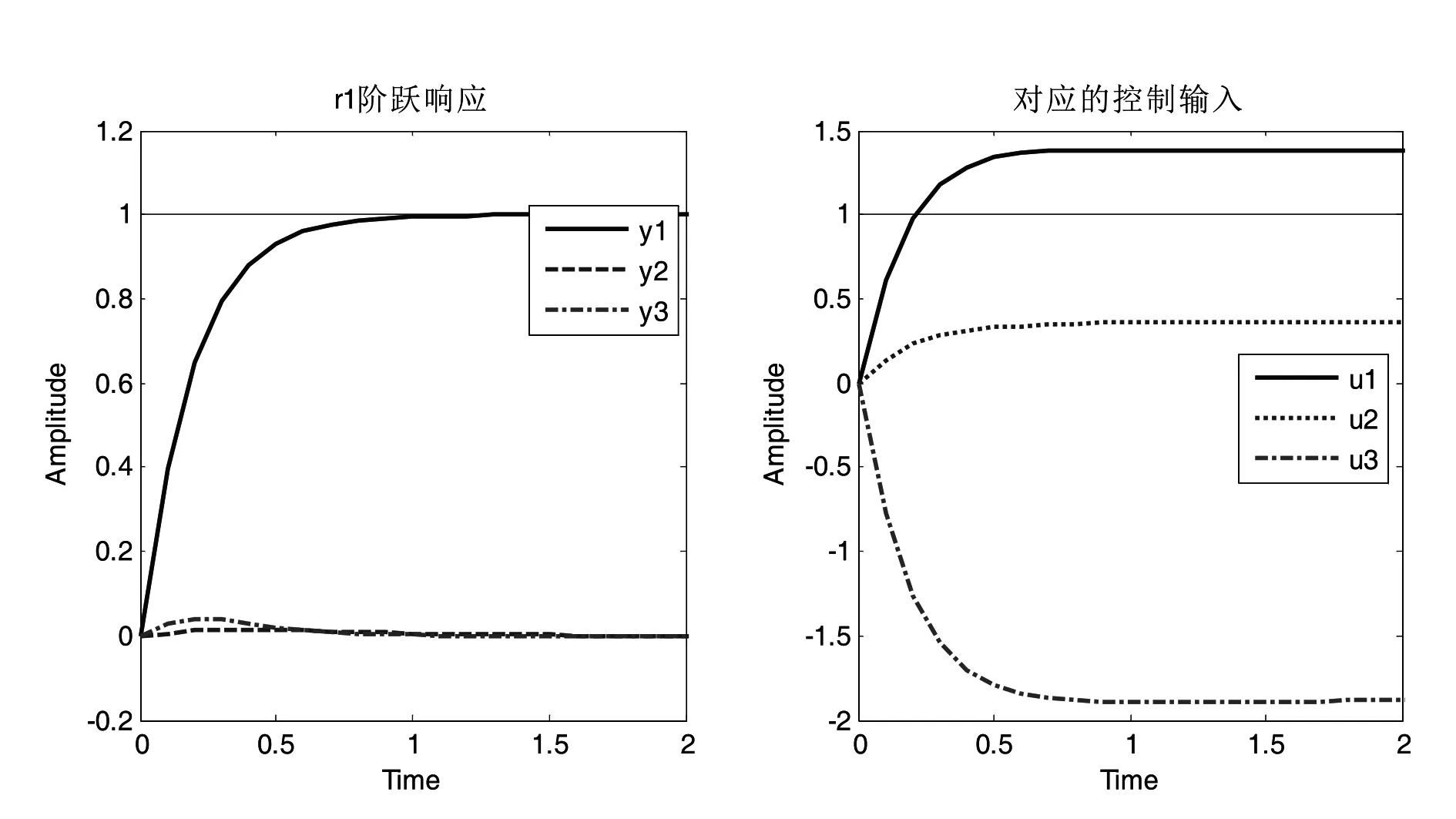
(a)r1的阶跃响应以及对应的控制输入

(b)r2的阶跃响应以及对应的控制输入

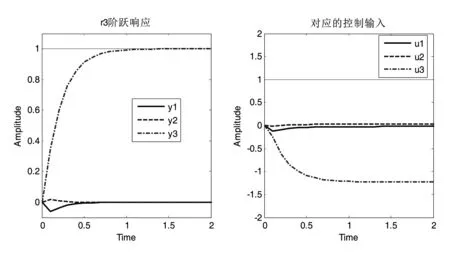
(c)r3的阶跃响应以及对应的控制输入图4 参考输入的阶跃响应

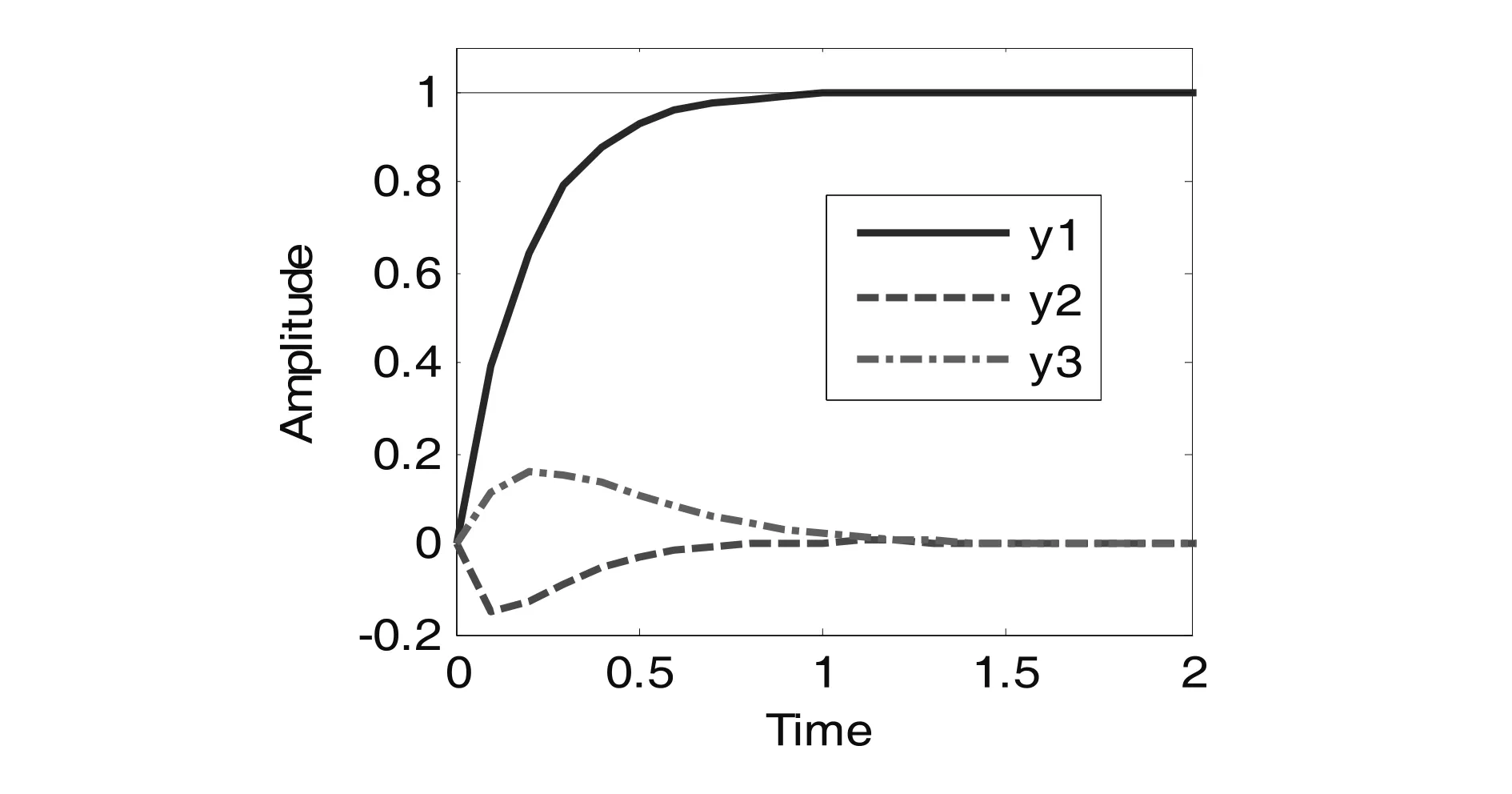
(a)r1的阶跃响应以及对应的控制输入

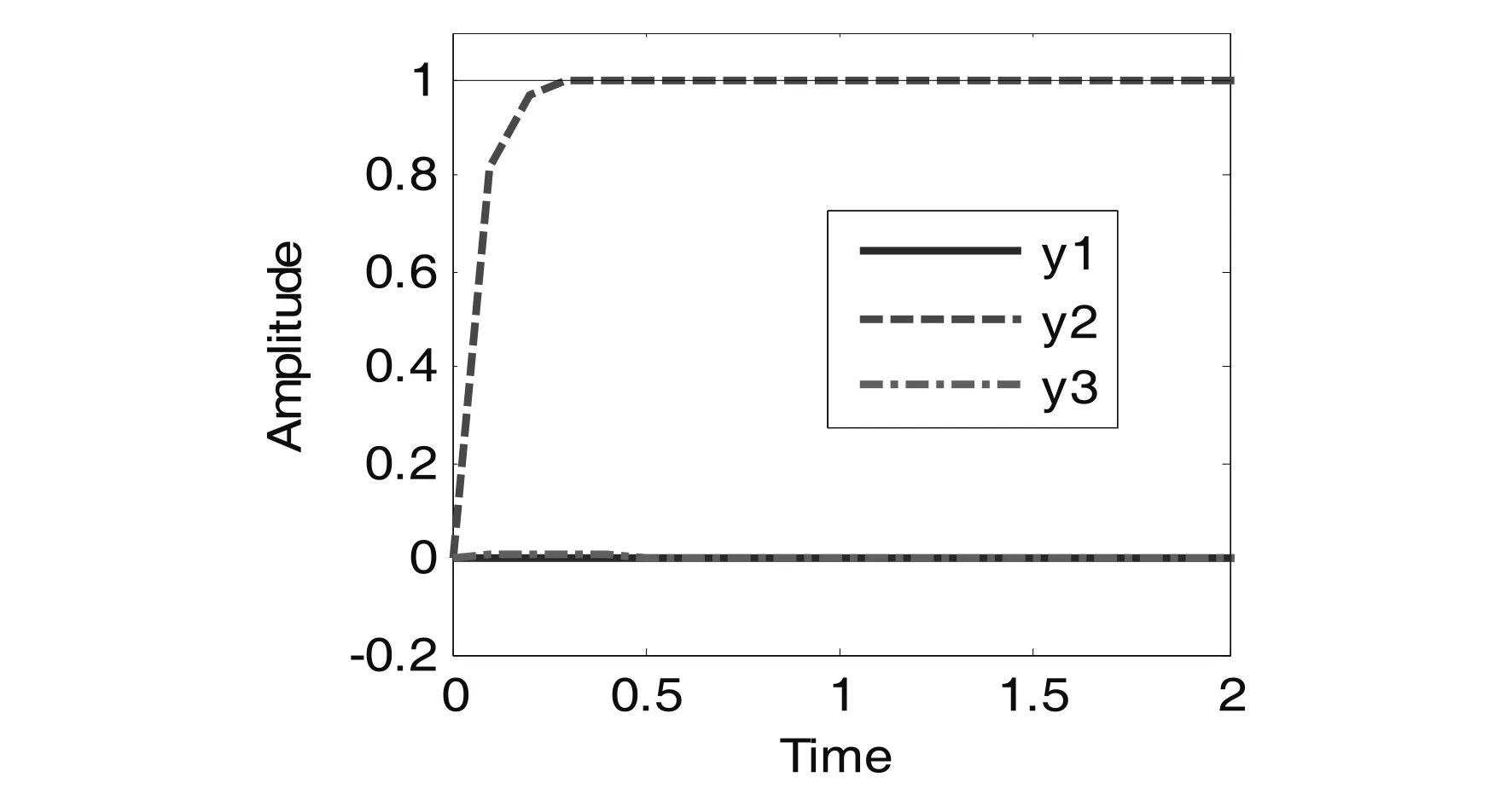
(b)r2的阶跃响应以及对应的控制输入

(c)r3的阶跃响应以及对应的控制输入图5 模型摄动不确定性仿真

对比图4和图5可知，当发动机的状态摄动范围在允许的范围内时，控制系统仍能保证快速地响应参考指令，并且系统的解耦能力依然很好，这说明系统能鲁棒镇定结构化摄动。

5 结 论

本文深入研究了将二自由度控制与H∞LSDP控制理论相结合的鲁棒控制算法，详细描述了设计步骤和过程。为了使系统具有良好的稳态跟踪能力和扰动抑制能力，设计了合适的前馈和后馈补偿器。将该方法引入到航空发动机控制中，并设计相对应的鲁棒回路成形二自由度控制器。仿真结果表明，系统解耦性良好，且系统的鲁棒稳定性和鲁棒性能均满足设计要求，同时系统对结构不确定性也具有良好的鲁棒性。