具有任意弹性边界单跨梁结构的振动特性分析

鲍四元，曹津瑞

（苏州科技大学 土木工程学院，江苏 苏州215011）

随着现代科学技术的发展，单跨梁结构在众多领域有着广泛的应用，如：机械、航空、航天、建筑与土木工程等领域。梁是道路桥梁、房屋建筑等工程结构中最基本的受弯承重结构，许多学者对其展开了深入的研究，而梁的振动特性又是国内外学者研究的热点方向。

对于梁的振动特性研究有多种经典方法。李麦侠[1]研究了梁的振动问题的离散格式，并用四阶龙格库塔法进行求解。梁利娜[2]等研究了原子力显微镜微悬臂梁的Timoshenko 梁弯曲振动，并利用差分法求解。王其申[3]等采用差分法建立了两端任意支承多跨梁的差分离散模型。程远胜[4]采用动力刚度法求出多跨梁在移动车荷载下的振动模态，用模态迭加法求解动响应。Kim[5]利用传统傅里叶级数建立欧拉-伯努利模型，通过控制微分方程和边界条件，得到梁的固有频率方程。Li[6]利用广义傅里叶级数法设置振型函数后代入控制微分方程从而得到精确度极高的近似解，但计算过程复杂。吴琛[7]采用双变量无单元法对欧拉梁进行自由振动的分析。

综上所述，目前的大多数研究局限于常规的边界条件，如：简支、固支、自由等，难以对任意弹性边界条件进行求解。边界条件作为重要的结构参数，对梁的振动特性具有重要的影响，尤其是弹性边界条件，传统方法研究弹性条件对振动影响的求解过程较为复杂。同时，传统的求解过程中往往根据边界条件而设置位移函数，这样当边界条件发生改变时需要重新推导位移函数再求解，不具备普适性，不利于展开研究。常见的位移函数存在着不能满足高阶次求解、截断误差导致数值不稳定、边界收敛性差等缺点。对此，石先杰和合作者[8-10]提出了新的数值求解方法来克服以上缺点，利用改进傅里叶级数建立梁、板等结构的位移函数。许得水和杜敬涛等利用改进傅里叶级数法研究了任意边界条件弹性杆结构的扭转振动分析[11]，并进一步扩展到非局部弹性杆的纵向振动分析[12]，获得了成功的应用。该方法适合任意边界条件，并且在边界处有良好的收敛性与精度。该文对于单跨梁，在梁两端引入平移与旋转弹簧来模拟任意边界条件，在此基础上，结合能量法建立梁的拉格朗日泛函表达式，得到梁的刚度矩阵与质量矩阵。通过求解特征值与特征向量从而获得单跨梁结构振动特性最为一般情况的预报，即获得单跨梁结构在任意边界条件下的若干阶振动频率以及模态振型。该方法具有快速求解、精确性高、可求解任意弹性边界条件的特点。

1 理论推导

1.1 梁振动模型

文中建立的任意边界条件下单跨梁的计算模型如图1所示。在梁的两端分别设置横向弹簧和旋转约束弹簧，参数k0、K0模拟x=0 处的边界条件，其中k0表示该处横向弹簧的刚度值，K0表示该处旋转约束弹簧的刚度值。类似地，参数k1、K1模拟x=l处的约束条件，分别表示横向弹簧和旋转弹簧的刚度值。当模拟简支边界条件时，只需将横向弹簧k0、k1的刚度值设置为无限大，同时将旋转约束弹簧K0、K1的刚度值设置为0。当模拟两端固定的边界条件时，只需将k0、K0、k1、K1的刚度值设置为无穷大（实际取一个足够大的数）。当刚度值k0、K0、k1、K1取有限值时，可模拟弹性不同边界的情况。

图1 任意边界条件下单跨梁结构的模型

1.2 改进傅里叶级数表达位移函数

使用改进傅里叶级数表达单跨梁的位移函数

从方程（1）可以看出，与传统傅里叶级数相比，该函数多出四项正弦式，函数在两端点位置上的一阶导数不再恒等于零。由于单跨梁的振动控制微分方程是四阶微分方程，式（1）中的辅助正弦项函数可使位移函数在整个求解区域内的三阶导数连续并且四阶导数处处存在。辅助函数的构造并不唯一，可以选择合理简便的辅助形式以降低计算难度。

1.3 能量表达式及求解

在建立位移方程后需要对相关未知系数进行求解，文中采用瑞利-里兹（Rayleigh－Ritz）方法。该方法可以求解整个结构的动力学问题，等同于对控制微分方程和边界条件联合求解。

单跨梁的拉格朗日泛函为

其中：V表示系统的总势能；T表示系统的总动能。

对于图1所示的结构，总势能为

其中：VP表示单跨梁储存的应变能；VS表示模拟边界条件的约束弹簧的势能，两者的表达式分别为

式中：E表示杨氏模量；I表示截面关于中性轴的惯性矩；k0表示左端横向位移弹簧的刚度值；K0表示左端旋转约束弹簧的刚度值；k1表示右端横向位移弹簧的刚度值；K1表示右端旋转约束弹簧的刚度值。

梁做简谐振动时，其动能最大值可表示为

式中：ρ 表示梁的质量密度；A表示梁的横截面积；ω 表示圆频率。

将式（1）与（3）－（6）代入式（2），对所得式中的系数Am、Bn分别求导数，并令所得导数为零，可得

式中：K为关于弹簧弹性系数的刚度矩阵，M 为质量矩阵。式（7）转换为求解特征值和特征向量问题，可以得到系统的振动特性。

2 结果与分析

由式（1）中可以看出，单跨梁结构的改进傅里叶级数位移表达式中存在无穷级数。为得到式（7）中的质量矩阵与刚度矩阵，需要对式（1）进行截断。截断级数M要使计算过程尽可能的简单，且计算结果尽可能的精确。另外模拟固定边界条件时采用无穷大数，即在程序编制中需要取一个足够大的数来模拟边界条件。在研究该方法的收敛性以及准确性时，构建如下梁：

梁的参数E、I、ρ、A都为1，采用标准国际单位。该节研究不同截断级数、不同无穷大取值对各种边界条件的影响。为了方便研究，采用C、S和F分别代表固支、简支和自由的边界条件。

对所有的频率和刚度进行无量纲化处理

2.1 经典边界条件下梁的振动特性

首先，考虑经典边界条件，即两端固定（C-C）和一端固定一端自由（C-F）。分别取截断级数4 至16，无量纲度无穷大数取104至1010。表1 和表2 分别给出不同截断级数M与无穷大数取值下C-C、C-F 梁的无量纲第一阶振动频率。可以发现，随着截断级数与无穷大数的增大，振动频率在极小的范围内震荡，可视为收敛。同时，在大于109时部分高阶频率出现复数。这是由于求解特征值时出现增根，得到负数解，对其开平方根后出现复数。虽然无穷数越大越能表现真实的固定边界条件，但是模拟发现通过此方法获得的振动频率只在一定范围内收敛。考虑到在处理大型矩阵运算时，不同的计算机、不同的求解软件会出现不同的计算结果，但一般情况下误差较小，对运算结果的影响不大。对于两端固定（C-C）与一端固定一端自由（C-F）边界条件，综合收敛性与准确性，无量刚度为无穷大数，运算中取为105或106，截断级数M取12。

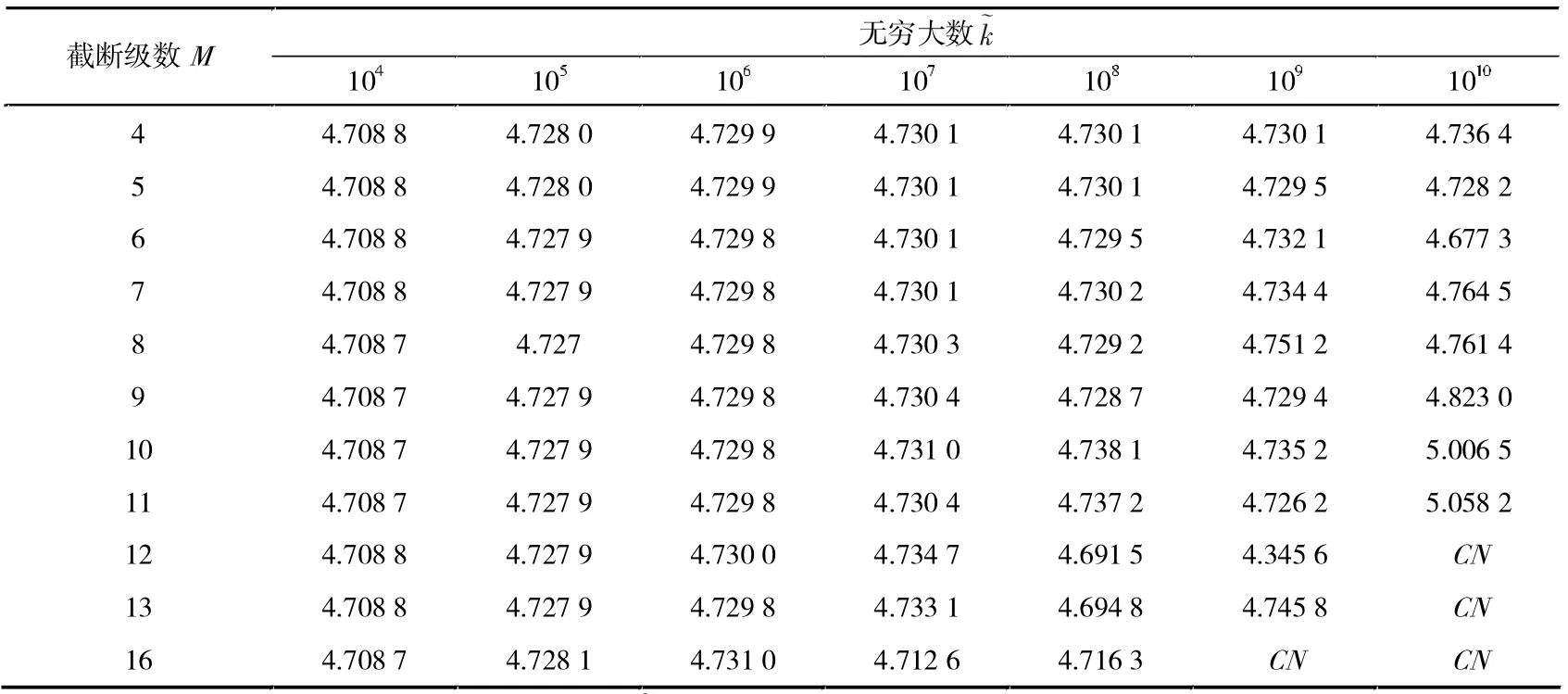
表1 两端固定（C-C）边界梁在不同截断级数下的无量纲第一阶振动频率ω*

两端固定边界（C-C）到一端固定一端自由边界（C-F）的变化过程可视作将一端边界约束进行逐渐释放的过程，即该端的边界约束刚度系数由无穷大逐渐减少到零。将刚度系数设置为0 至106之间的任一值可以来模拟固定-弹性的边界条件，也可将梁的左端的边界约束进行释放，从而模拟弹性-弹性的边界条件，进而实现了任意边界条件的求解。计算中只需设置不同的弹簧弹性系数，即可得到任意边界条件下的振动特性。

表2 一端固定一端自由（C-F）边界在不同截断级数下的无量纲第一阶振动频率ω*

2.2 固支-弹性边界条件下梁的振动特性

先将上一节中的两端固定边界（C-C）中的一端进行释放，即模拟固定-弹性边界条件。首先，按照解析方法得到在自由端有一个弹性支承的悬臂梁的频率方程[13]

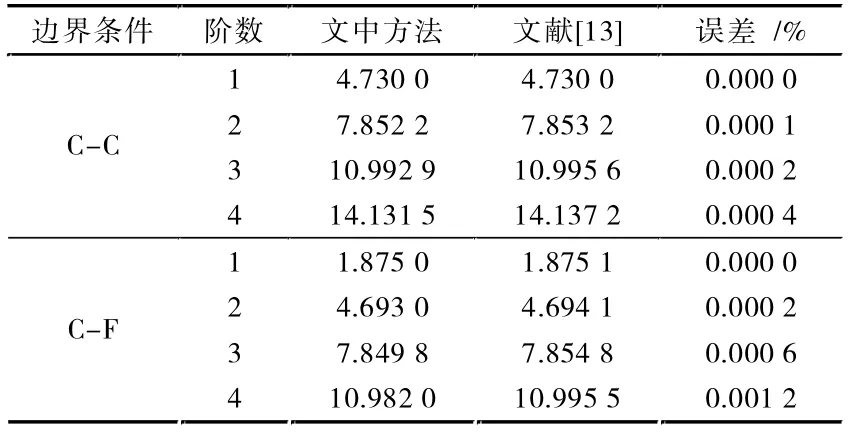
表3 两种边界条件下梁前四阶无量纲频率及误差

式（11）的根βi对应梁的振动频率ωi，i为模态序数。分别设弹性支座处为125、150、300、1 000为0，固定支座处无穷大数取106，截断级数为12，将文中得到的频率与文献[13]比较。表4 中给出了通过此方法与解析法得到的无量纲频率。由表4 可知，此方法与解析法最大误差仅为0.000 4%。该算例说明了此方法不仅适用于经典边界条件，还适用于任意边界条件下的单跨梁振动特性的求解，进一步验证了此方法的准确度。

图2 给出了固定-弹性边界条件下梁的前六阶振动频率随着右端位移弹簧的刚度值的变化情况。从图中可知，弹性边界约束刚度对于梁的振动频率有着重要的影响。这种影响不是均匀的，对于第一阶可以明显的看出，当刚度值在0 至150 之间时振动频率变化的比较剧烈。对于不同阶态，阶数越高，刚度值对于振动频率的影响越小。在图2中的第六阶的无量纲振动频率，是一条较为平缓的直线。

表4 固定-弹性边界条件下无量纲频率误差分析

图2 固定-弹性边界条件下第M（M=1，2，…，6）阶振动频率随边界约束刚度的变化

2.3 模态振型

如上文1.3 节所述，在求解单跨梁结构的特征值问题时除了可以得到振动频率，还可以得到特征向量。将各阶特征向量代入式（1），即可绘制对应阶的振动模态曲线。现给出简支-简支、固定-弹性边界下梁的模态振型图，如图3所示。截断级数M=12，无穷大数取106，弹性边界的无量纲刚度系数为300。

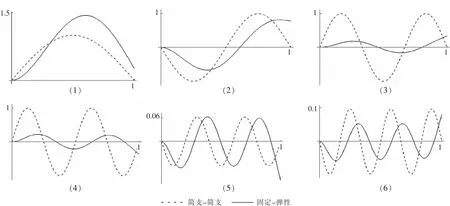
图3 两端简支和固定-弹性边界条件的前六阶模态

3 结语

采用改进傅里叶级数建立了梁的任意边界条件下振动特性模型。通过两端设置横向弹簧与旋转弹簧来模拟任意边界条件，在求得质量矩阵以及刚度矩阵后，设置不同的弹簧刚度值以及梁的力学参数，通过求解特征值与特征向量获得梁的振动频率以及模态振型。与传统傅里叶级数相比，使用改进傅里叶级数可以有效改善传统傅里叶级数在边界存在导数不连续的问题，并且提高了精度。

在数值运算方面，当边界条件发生改变时该方法不像解析法需要重新推导。通过设置用户交互界面，实现用户输入相应的边界条件及其他参数，自动显示出振动频率以及模态振型，所得结果直接、准确性好、计算简洁方便。因此，该方法在实际工程中有着重要的应用价值。