利用DLG图提取河流名称的方法及实现

雷雨婷，李林燕

（1.苏州市智慧城市规划研究应用中心，江苏 苏州215004；2.苏州经贸职业技术学院 信息技术学院，江苏 苏州215009）

DLG 包含了各地理要素的空间信息和相关属性信息，是最重要、使用最广泛的基础地理数据。在苏州市已建成的数字苏州地理空间框架项目中整合更新了苏州市域1∶25 万、1∶5 万、1∶1 万、1∶1000、1∶500 数字线划地图（DLG）数据，它是基础地理信息数据库的重要数据来源，并为各行各业提供坚实的数据保障。注记要素是数字线划图（Digital Line Graphs 简称DLG）重要的组成部分，表示了地理要素的属性信息。空间信息主要是表示要素的位置、形态、大小分布等内容，是进行空间分析和研究的基础[1-2]，而注记包含的属性信息起着补充和丰富空间数据的作用。

河流名称注记是河流图形重要的属性信息。DLG图注重的是合理、美观的表达图面要素，并不注重要素与要素之间的相互关系。在苏州DLG图中，水域要素图形包括河流、湖泊、水库等，它是面要素，河流名称是逐字打散后有规律地标注在对应的面要素内部，河流与注记、注记与注记之间只是视觉上是有关联的。这样导致直接提取的河流名称很多都是无效的，不能作为基础数据提供给地理信息应用和服务进行使用。

现有文献对注记的研究主要集中在两个方面：一是从栅格地图中识别并提取英文或数字注记方法的研究[3-5]；二是对注记自动配置方法的研究，例如通过数学形态学来确定点线面状注记位置[6]，通过长对角线法实现面状注记的自动配置[7]，以及根据点线面要素的特点来制定注记自动配置策略[8]等。这些研究表明注记的排列配置都有规律可循。

DLG图中的河流注记属于面状注记，面状注记排列的规律主要是沿骨架线进行排列[9-10]，河流骨架线方向也就是河流走向。笔者通过对DLG图中河流名称逐字沿河流走向配置的规律进行分析，提出先对河流注记之间的距离进行聚类分析，然后根据聚类结果生成可能的注记组合，最后实现河流名称的提取并通过核查确保河流名称的准确性。

1 DLG图中河流注记聚类分析

DLG图中河流面与河流注记的空间关系如图1 所示，根据河流注记的排列及其与河流面的空间关系，可将河流注记配置的规律归纳如下：

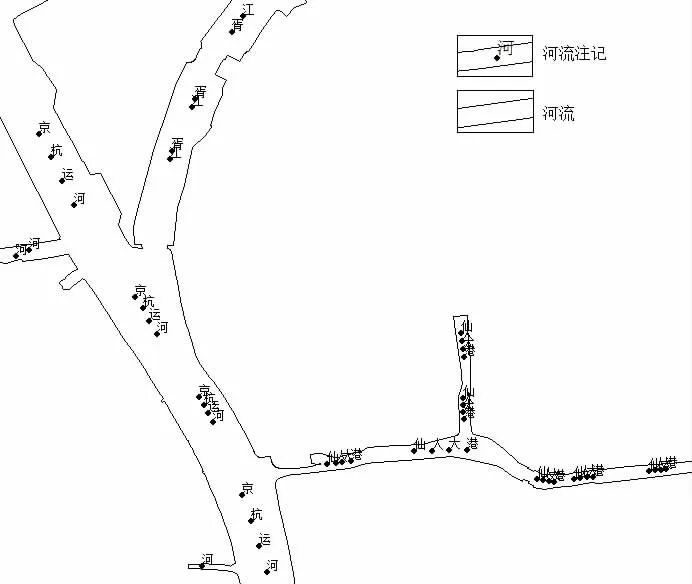
图1 河流面与注记

（1）河流名称分解成单个文字进行标注；

（2）单个文字的注记沿河流面的走向进行排列；

（3）完整的河流名称注记内部等距离分布，不同的河流名称注记之间的距离变化很大。

除上述三类一般性规律外，DLG图中的河流注记及其与河流面之间的关系还存在以下几类特殊情况：

（1）存在大量的“河”、“塘”等无效文字注记，即无实际意义的河流注记；

（2）一个完整的河流名称可能是多个注记要素，也可能是一个注记要素；

（3）一个完整的河流名称注记可能分布在两个或多个河流面内。

1.1 基于点要素间距离的聚类方法

对河流注记进行聚类的主要思路如下：以一个河流面要素为基本面，按基本面进行分组，基本面内的所有注记作为聚类分析的一个单元，不同基本面内的注记分别进行聚类分析。

将注记视作点要素，通过设定点要素的距离、邻域、类别、方向四个特征值来对其进行分析，点要素i的特征值定义如下：

（1）距离特征值d：点要素i的距离特征值是指该点与其他所有点要素之间距离的最小值dimin。

计算点要素i的距离特征值的问题可以描述如下：对于目标点集P={p1，p2，…，pn}，定义dij为点要素pi到集合P中点要素pj的距离，那么距离特征值可写成如下公式

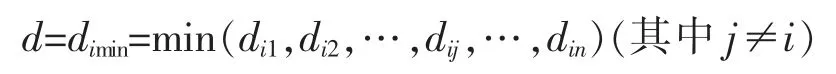
文中根据目标点集P中的点构建的Delaunay 三角网，计算点要素i的距离特征值。Delaunay 三角网在满足四点不共圆的前提下具有唯一性，且由Delaunay 三角网的最接近性可知任意一点将与其相距最近的点连接形成三角网中的一条边作为基线[11-12]（如图2所示）。故可通过计算三角网中点要素i关联的所有边的长度，找到最短的长度值作为点要素i的距离特征值d。

图2 根据点集生成的约束delaunay 三角网

（2）邻域特征值n：点要素i的邻域定义为以点要素位置为中心，以一定距离S为半径，生成的圆形缓冲区Ni所覆盖的区域。若没有其他点要素在点要素i的邻域内，则n=0；反之，n=1。

（3）类别特征值t：若点要素j的位置在点要素i的邻域内，且点要素j的距离特征值djmin在点要素i的距离阈值内，则点要素i与j为同一类别t（如图3所示）。

（4）方向特征值a：定义点要素i的方向特征值a的值域为{-1，1}（其中-1 表示方向应为从北到南，1 表示方向应为从西向东），若点要素j是点要素i相距最近的点，当直线段Lij的斜率K大于1 或小于-1 时，a为-1，当直线段Lij的斜率K大于-1 且小于1 时，a为1（如图4所示）。

图3 判定为同一类别的情况

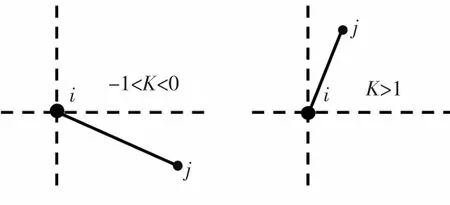
图4 判定方向特征值

1.2 基于要素间距离的聚类实现

根据河流注记配置规律及上述点要素聚类方法，并考虑注记的几种特殊情况后，文中提出的注记聚类方法按如下步骤实现（如图5所示）。

步骤1判断一个注记点要素i的字符数是否等于1。若是点要素i单个字符即字符数为1 （如图6所示），则开始计算其距离特征值，转步骤2；若是点要素i的字符数大于1（如图7所示），则判断为完整的河流名称注记，不做处理。

图5 聚类流程

图6 字符数为1 的四个注记点要素

图7 字符数大于1 的一个注记点要素

步骤2计算点要素i与其所在基本面内其他点要素之间距离的最小值，得到距离特征值dimin（如图8所示），设置距离阈值的范围在（0.67*dimin，1.5*dimin）之间，跳转步骤3。

步骤3根据距离特征值dimin设置点要素i 的邻域，其缓冲区距离S=1.5*dimin（如图9所示设置邻域范围），跳转步骤4。

图8 计算点要素的距离特征值

图9 设置邻域范围

步骤4判断点要素j是否位于点要素i的邻域Ni。若不满足条件，则点要素i与j不属于同一类别；若满足条件，则点要素i的邻域特征值ni=1，跳转步骤5。

步骤5在满足邻域条件下，判断点要素j的距离特征值是否在点要素i的距离阈值内。若不满足条件（如图10所示，左边距离较远的“河”的邻域特征值n=1，但其他注记的距离特征值都不在其距离阈值内），则点要素i与j不属于同一类别；若满足条件，则跳转步骤6。

步骤6按如下方式判断要素i与j最终是否属于同一类别：若点要素i与h属于同一类别tih，且点要素j与h属于同一类别tjh，则点要素i，j，h均属于同一类别。若点要素i存在至少1 个同一类别要素，则跳转步骤7；若不存在，则删除此点要素（如图10所示）。

步骤7计算点要素i的方向特征值ai。根据点要素i的同一类别ti中任意两点连线的斜率K值，计算ai（如图11所示，“京杭运河”方向a值为-1，“仙人大港”方向a值为1），转步骤8。

步骤8按照ai确定的方向，将与点要素i同类别的注记合并成完整的河流名称（如图11所示）。

图10 竖直走向的“京、杭、运、河”属同一类别，左边距离较远的“河”应删除

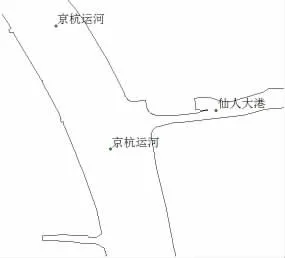
图11 注记合并成河流名称示例

由于FME 软件可以实现多种格式数据的读取、处理和存储等操作，其支持格式包括Autodesk AutoCAD DWG/DXF（dwg 格式）和Esri Geodatabase （File GeodbArcObjects）（gdb 格式）等，数据的处理包括数据量的增加删减、几何图形及属性结构的修改、叠置分析及Delaunay 三角网的生成等。文中采用FME 软件来实现上述各步骤（如图12所示），并将最终数据存储为gdb 格式，以便在地理信息应用和服务中使用。

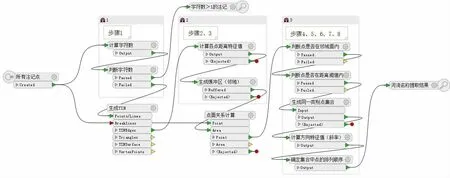
图12 FME 实现上述各步骤

2 利用DLG图中注记提取河流名称

文中选择苏州市部分区域河流DLG 数据进行试验，该区域河流水系集中且丰富。该实验选取了大约4 900 多个注记要素，河流基本面约2 900多个（如图13所示）。

图13 部分选取的注记和河流

依照本聚类方法，最终提取了约1 000多个完整的河流名称，对河流名称提取的正确率约为96%，具体数据见表1。其中出现部分提取错误的原因主要是：DLG图中河流名称标注错误，当计算的方向特征值在45°左右时不能准确判断注记排列方向，河流名称标注的距离不符合文中描述的规律，同一河流面（基本面）内河流名称标注不全。按照文中所述方法提取河流名称完成后，可将判断错误的注记按照正确的河流名称表进行修正。

3 结语

笔者提出了一种基于要素间距离的聚类方法，该方法的主要特点是通过研究DLG图中河流注记的配置规律，利用注记之间的距离关系，准确地提取河流名称。此外，河流名称提取完成后，将提取后的名称与河流面按空间关系关联，仍不能保证完全正确。这是因为在DLG 制图过程中，有同一河流面中配置了多个不同名称注记，特别是在河流分岔处。因此，在整合河流的图形和属性信息时，仍需按实际情况对河流名称、河流的对应关系进行进一步的处理。

表1 河流名称聚类结果