一种非完全标注的文本分类训练方法*

段军红，李晓宇，慕德俊

（西北工业大学深圳研究院, 深圳518057）

1 引 言

对于完全标注的文本，通过深度学习、分布式随机森林、梯度提升决策树等分类方法在标准测试集上能实现较高精度的文本分类[1]。但在当前的分类体系下，对于非完全标注的文本分类器，无法有效识别出某类别与其它类别的边界，甚至这些类别本身就是与其它类别重合的。在标准测试集上性能良好的分类算法，往往在实际数据分类中性能表现不佳。分类器性能低下的原因在于样本分类体系不满足互斥原则[2]。例如，类别名称中既包括“中石油”、“中石化”等以关注对象为分类基准的类别，又包括“国内新闻”、“国外新闻”等以事件地点为基准的类别，以及各种其它栏目划分方法，分类标准非常不统一。在不统一的分类标准下，一篇文档完全可能既属于“中石油”，又属于“国内新闻”，但在信息采编中，出于避免重复的原因，编辑最终要将文章仅划归在一个栏目下。这种由于分类逻辑上的不统一以及文章内容本质上的多样性，最终将导致分类器无法得到与训练数据一致的分类。

总之，由于样本数据类别标示不完备，每个样本仅标识了实际所属分类中的一个，导致机器学习训练出的分类器性能低下，这就是“非完全标注”带来的问题。针对此问题，将原来的分类体系拆分成多个分类体系，使每个分类体系下的类别是互斥的，再在每个拆分出的分类体系下，对数据进行训练，可提高分类器的精度[3]。而多个分类器并联，分别输出样本对应的类别，即可得到样本实际所属的所有类别。

2 基于遗传算法的最优分组

2.1 最优类别分组

将原始分类拆分为多个分类体系的最优组合，是指将原始分类拆分成相互独立的多个分类体系的组合，使得在每个分类体系中，该体系内包含类别的训练样本通过指定的分类器误分数量之和最小[4]。

按照一般监督学习的定义[5-6]，给定包含N 个训练样本的训练集{(x1,y1),(x2,y2),…,(xN,yN)}，其中xi是第i 个样本的特征向量，yi是第i 个样本的类别序号，yi∈{1,2,…,M}，分类学习算法就是在假设空间（Hypothesis Space）中寻找一个函数g：X→Y，其中X 是输入空间，Y 是输出空间，使得对于一个指定的评分函数（Scoring Function）f：X×Y→R，函数g 可以返回使得评分函数取值最大的y，即gg(xx）=。

为了表征函数与训练集的拟合程度，一般均会定义一个损失函数（Loss Function）L：X×Y→R≥0，以及一个风险函数（Risk Function），定义为损失函数的期望值，该期望值可通过训练样本进行估计，即。此外，为了防止过拟合，在训练时还会引入正则化惩罚因子（Regularization Penalty）先验分布C(g)，常见的选择包括L1范数、L2范数等。因此，分类学习算法即是在假设空间中寻找一个函数g 使得结构化风险J(g)=Remp(g)＋λC(g)最小。

而在“非完全标注”问题中，则是要寻找一个输出空间（分类标签）的K 划分，使得对任意的α≠β均有，且通过给定的监督学习算法生成K 个映射gi：X→Yi,i=1,2,…,k，使得J(gi)最小。

机器学习训练过程时间复杂度一般较高。若在优化的每一个迭代过程中均需要对训练后的结构化风险J(gi)进行计算，则计算事件复杂度往往会增大到不可接受的程度。对于分类训练后得到的融合矩阵，由于其表征了经过特定的监督学习算法后的样本标注类别与训练出的分类器预测的类别之间的差异，因此，可直接采用训练数据的融合矩阵作为最优化分组的依据[7-8]。

在分类问题中，希望对于整个训练集而言，错分类的样本数量占所有样本数量的比例尽可能小。在分组后，设置实际优化目标如下：

设融合矩阵SN×N=[si,j]，矩阵中元素si,j为标注为第yi类但经过给定分类算法预测为第yj类的训练样本数量。那么，最优分组是寻找一个类别集合Y 的K划分且YYαα∩IYYββ==Φ∅，可使得误分率ER=最小化。

例如，图1 为A、B、C、D、E 五个类别的融合矩阵，显然，仅有对角线上的元素S1,1,S2,2,…,S5,5为正确分类的样本数量，其它元素均为误分类，那么，整个样本集在该分类器下的误分率即为：

若将所有类别做一个2-划分，例如，{A,C}划分为一组，{B,D,E}划分为一组，那么，在{A,C}组内，s1,1+s3,3仍为正确划分的样本数量，而错误划分的样本数量为s1,3+s3,1。同样，在{B,D,E}组内，s2,2+s4,4+s5,5为正确划分的样本数量，s2,4+s2,5+s4,2+s4,4+s5,2+s5,4则是错误划分的样本数量。故此，在这种划分下，样本的误分率为：

而优化目标，则是找到一个最优的划分，使得误分率达到最小[9-10]。

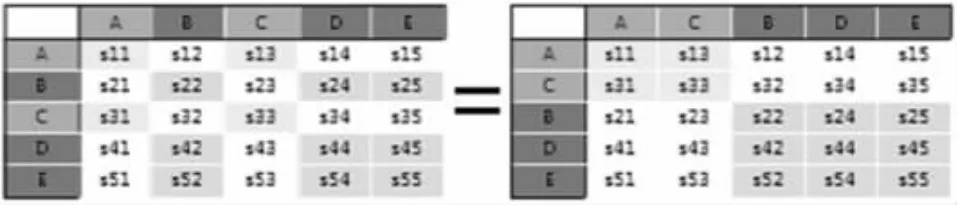
图1 分组优化目标

2.2 遗传算法

在明确最优化目标后，要设法对这一优化过程进行计算。首先，需要评估的是解空间的大小。在确定分组数量K 的前提下，将N 个元素分为K 组，每组至少包括一个元素，其组合数量为第二类Stirling数S（N,K），其递推计算公式为：

以50 个类别分为3 组为例，有：

S(50,3) =4,081,990,278,659,592,354

显然，对此不可能通过穷举遍历的方式进行，需要采用一种优化算法[11-12]。遗传算法是一类借鉴了进化生物学中的一些现象发展出来的最优化方法，是进化算法的一种。在遗传算法中，优化问题的解被称为个体，表示为变量序列，一般称其为染色体（Chrome）。染色体一般表达为简单的字符串或数字串，这一过程称为编码。算法在起始时随机生成一定数量的个体，在每一代中，每一个个体都被评价，并通过计算适应度函数得到一个适应度数值。随后，按照一定的选择策略（一般而言适应度越高被选中的概率越高），选择一定量的个体进入繁殖阶段。在繁殖阶段中一般包括交叉（Crossover）与变异（Mutation）两个算子。交叉是指在一定的交叉概率下（一般范围是0.6~1），两个被选中的个体的染色体在交配点互换，生成两个新的染色体以代替原有个体；而变异则是指按照一定的变异概率（通常小于0.1）在随机位置改变原有染色体。通过多次迭代，新产生的个体一代代向增加适应度的方向发展，直至得到满足条件的解。算法过程如图2 所示。

图2 遗传算法

在最优分组问题中，设遗传算法相关要素如下：

(1) 融合矩阵：采用GBM 算法训练生成的融合矩阵；

(2) 编码方式：采用整数编码，染色体长度为类别数量N，染色体上每条基因的取值范围为{1,2,…,K}，其中K 为分组数量，染色体上取同一个值的类别代表分在同一组内，这样一条染色体就代表一个可行解，并且所有的可行解均可用染色体来表示，任意染色体经过交叉和变异算子处理后，生成的子代仍为可行解；

(3) 适应度函数：由于遗传算法是选择适应度高的个体，因此不直接采用误分率ER 作为适应度，而是采用正确率P=1-ER 作为适应度；

(4) 种群数量：10000 条；

(5) 交叉概率：0.35；

(6) 变异概率：1/12；

(7) 最大迭代次数：100 次；

(8) 样本数量：184415 个（删除了样本个数过少的类别）；

(9) 类别数量：101 个（删除了样本个数过少的类别）；

(10) 分组数量：3 组。

经过遗传算法计算，在第100 代时，适应度达到了0.9343。

按照计算出的分组，对各个分组进行了GBM 分类训练，组内训练结果如表1 所示。

表1 组内分类效果

可以看出，在各个分组内，分类器的分类效果都明显优于未分组前。即组内的类别对于该分类算法而言，具备较好的可区分性，类别独立性较强，重叠性较低。由此可确定，该分组方式可以达到将原始分类拆分成相互独立的多个分类体系组合的作用。将通过三组数据分别训练出的分类器对所有数据进行标注，且若认为任一个分类器给出的标签符合原始标签即认为分类正确，则得到的分类正确率即为1－0.2174＝78.26%，准确度有明显的提升[13]。

以图3 所示的页面作为一个实例，对分类器给出的标签进行主观判断。从抽样结果看，标签的合理性可以得到肯定[14-15]。例如，在原始样本中，《胜利油田高温分布式光纤测温技术成功应用》一文被划归在“石油科技·科技动态·物探测井”栏目下，而经过最优分组后，该文还被识别为“石油科技·科技动态·勘探开发”以及“工程服务·物探测井”等几个额外类别。

图3 分类实例

3 分组数量确定

通过指定分组数量，利用分类算法在测试集上的融合矩阵，即可借助例如遗传算法来获取最优分组，解决由于样本标注不完全带来的分类器性能低下的问题。

随着分组数量的增加，最优分组对应的适应度逐渐增加，但增加趋势逐渐变缓。最优分组需要指定分组数量K，可以通过计算不同分组数量下的适应度，从而得到适当的分组数量。

通过分析可以发现，按照上述方法获得的最优适应度，与二项分布规律高度吻合：在最优K 分组上的适应度，近似等于分类算法在K 次分类实验中至少成功一次的概率。从数据上看，两者非常吻合。

对之前提及的其它分类算法，包括深度学习、分布式随机森林等都进行了基于融合矩阵的最优分组，可得到类似的结论。因此认为，基于融合矩阵的最优化分组，可以解决由非完全标注带来的分类器性能下降的问题，并得到了具备一定通用性的两步分类框架：

(1) 利用分类算法对训练数据进行训练，得到针对训练集的融合矩阵S 以及精确度p;

(3) 以最大化正确率为优化目标，采用优化算法（如遗传算法等）计算最优分组方案；

(4) 按照最优分组，采用与之前相同的分类算法以及算法超参数，分别训练各组数据的分类器；

(5) 并联分类器，对每一个待分类样本进行分类，得到的分类结果均作为该样本的类别标签。

表2 为根据中国石油天然气集团公司（China National Petroleum Corporation, CNPC）语料库选用梯度增强机（Gradient boosting machine, GBM）分类算法获得的融合矩阵，进而通过遗传算法得到的分组数量（第一行）与适应度（第二行）的关系，表中第三行为依据二项分布X~B(K,p)计算出的K 次贝努利实验至少成功一次的概率prob=1- （1- p）K，其中p 为GBM 分类算法对未分组的整个数据集进行训练后得到的分类器的精确度。在其它数据集上也发现了类似的规律。

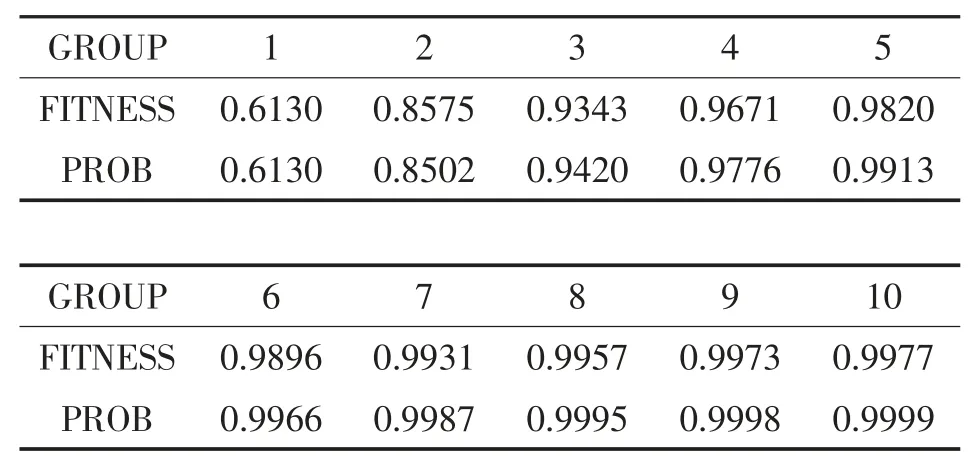
表2 分组数量的经验分布与实际分布

按照上述规律，就可以直接估计达到指定的适应度阈值所需的分组数量，即：

适应度越高，意味着分类器在分组后的训练集上表现越好，同时在验证集上也能表现出较好的性能，例如在对CNPC 语料库进行最优5-划分后，分类器在验证集上的精度提升至88.61%，较3-划分上的精度78.26%又有较大提升。

4 结束语

在当前分类体系下，非完全标注的文本分类器无法有效识别出与其它类别的边界，甚至这些类别本身就是与其它类别重合，造成实际数据中分类性能低下。针对此类问题，通过最优类别分组和遗传算法，尝试建立了一种非完全标注的文本分类训练方法，将原来的分类体系拆分成多个分类体系，使得每个分类体系下的类别彼此互斥，在每个拆分出的分类体系下，对数据进行训练，提高分类器的精度。经过多个分类器并联，分别输出样本对应的类别，就可以得到样本实际所属的所有类别。通过中国石油天然气集团公司语料库选用梯度增强机分类算法获得的融合矩阵，用所提方法进行了仿真，结果表明：适应度越高，分类器在分组后的训练集上表现越好，同时在验证集上也能表现出较好的性能，分类器在验证集上的精度有较大的提升，证实了该方法的有效性。