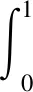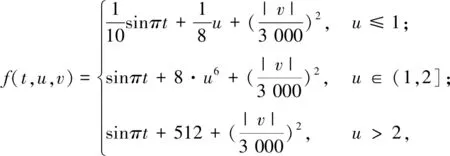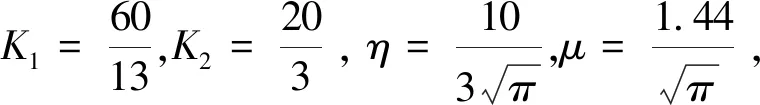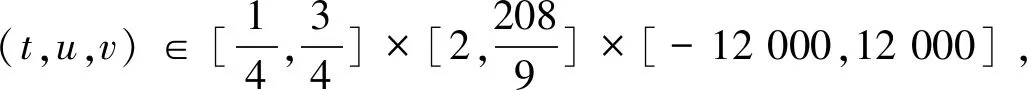带有积分边值条件的分数阶微分方程正解的存在性
,,
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
近年来,分数阶微分方程被广泛应用到各个研究领域,如流体力学、生物数学、控制和工程等。许多学者对分数阶微分方程解的存在性问题做了大量研究,并且已经获得了很多成果[1-17]。其中,不少文献研究带有积分边界条件的分数阶微分方程正解的存在性[1-4,7-8,12-17]。
文献[1]研究了一类具有积分边界条件的分数阶微分方程边值问题正解的存在性,通过利用Guo-Krasnoselskii不动点定理得到了该问题至少有一个正解存在。文献[2]研究了具有非局部项的奇异非线性共轭型分数阶微分方程正解的存在性,通过建立极大值原理、构造上下解并运用Schauder不动点定理得到了至少有一个正解存在的充分条件。文献[3]利用单调迭代方法及与格林函数有关的不等式获得了非线性分数阶边值问题有两个非平凡解的存在性,而文献[2-3]的边界条件里都含有Riemann-Stieltjes积分。文献[4]和[7]中,作者运用Leggett-Williams 不动点定理得到了Caputo型分数阶微分方程多个正解的存在性,且文献[7]运用Guo-Krasnoselskii不动点定理及上下解方法获得了该问题正解的唯一性和存在性。文献[8]中,作者运用上下解方法及Leray-Schauder度理论获得了分数阶微分方程的积分边值问题至少有三个正解的存在性。
从上面的文献分析可以看出,研究带有积分边界条件的分数阶微分方程的相关成果已经有很多。但是,这些工作均建立在非线性项中不显含导数项的前提下。而本研究方程的非线性项中显含一阶导数项,这是与以上所有文献的不同之处。以上文献处理带有积分边界条件的分数阶微分方程所使用的方法不适用于处理非线性项中显含一阶导数项,而本文给出了该问题的处理方法。此外,给出的非线性项条件比文献[4,7]中的更弱,是对现有文献的一个推广,也更具有普遍性。
本文研究如下分数阶微分方程边值问题解的存在性:
(0.1)
u(0)=u(1)=0;
(0.2)
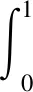
(0.3)
其中f:[0,1]×R+×R→R+,α1>β1>0,γ1>δ1>0,g,h∈C([0,1],R+), 导数。运用推广的 Leggett-Williams 不动点定理,得到了边值问题(0.1)~(0.3)至少存在三正解u1(t),u2(t),u3(t),最后给出数值例子来验证给出结果的正确性和有效性。
1 预备知识
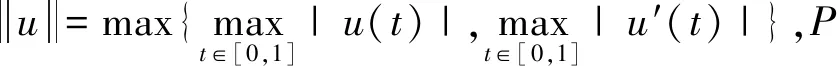
定义1.1设γ:P→[0,∞)是P上的一个非负连续泛函,若对所有x,y∈P,0≤t≤1,有γ(tx+(1-t)y)≥tγ(x)+(1-t)γ(y),则称γ为P上的一个非负连续凹泛函。
定义1.2设α:P→[0,∞)是P上的一个非负连续泛函,若对所有x,y∈P,0≤t≤1,有α(tx+(1-t)y)≤tα(x)+(1-t)α(y),则称α为P上的一个非负连续凸泛函。
设α,β:P→[0,∞)是两个非负连续凸泛函,对给定正常数r,L,M,以及u∈P,有
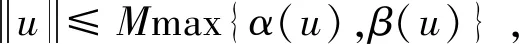
(1.1)
Ω={u∈P|α(u) (1.2) 显然Ω是P上的非空有界子集。 定义1.3[9]给定常数r>a>0,L>0,α,β:P→[0,∞)满足(2.1),(2.2),γ是P上的一个非负连续凹泛函,定义如下有界凸集: P(α,r;β,L)={u∈P|α(u) P(α,r;β,L;γ,a)={u∈P|α(u) 引理1.1[11]微分方程 u″(t)+y(t)=0,0 u(0)=u(1)=0, 且G(t,s)有如下性质: 1)G(t,s)≤G(s,s),0≤t≤1; 本文始终假设如下条件成立: (A0)κ=κ1κ4-κ2κ3>0,κ1≥0,κ4≥0,其中 引理1.2[4]微分方程 引理1.3[4]令 则有: 由引理1.1和1.2易得如下结果。 引理1.4微分方程(0.1)~(0.3)对应的线性方程 u(0)=u(1)=0, 本节将运用推广的 Leggett-Williams 不动点定理来得到问题(0.1)~(0.3)的解。 则问题(0.1)~(0.3)至少有三个正解u1,u2,u3,满足 因此 对于 结合引理1.1,引理1.3及(A3),有 因此(2.1)式满足定理1.1中的条件(iii)。 考虑如下形式的边值问题: (3.1) u(0)=u(1)=0, (3.2) (3.3) 其中,q=3.5,α1=γ1=2,β1=δ1=1,h(t)=t3,g(t)=t2, 经验证: (H1)~(H3) 满足定理2.1的所有条件。因此问题(3.1)~(3.3)至少存在三个正解。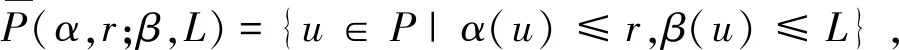
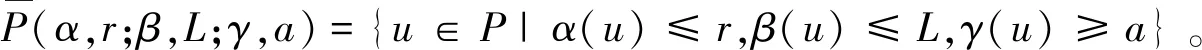
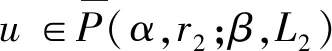
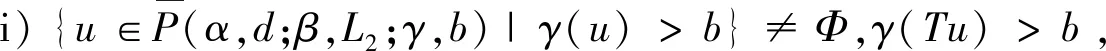
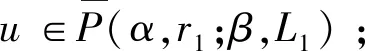
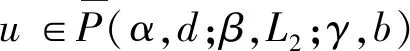
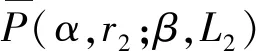
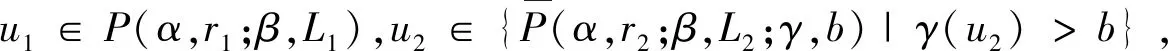
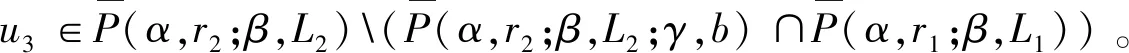
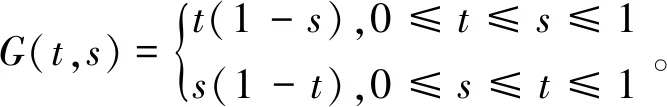
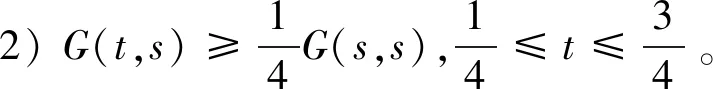

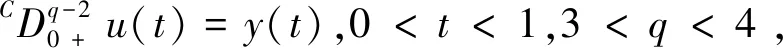
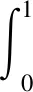
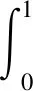
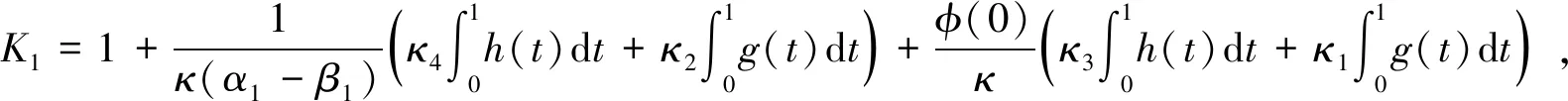
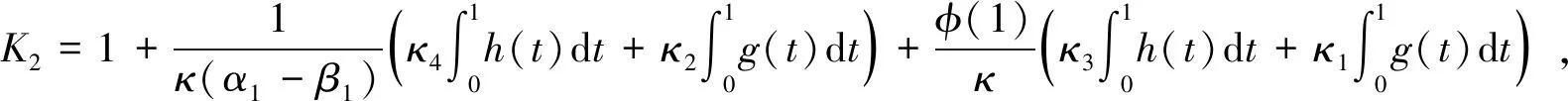
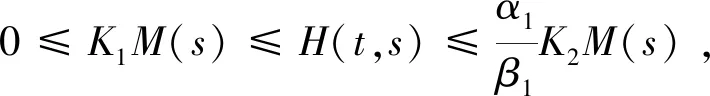
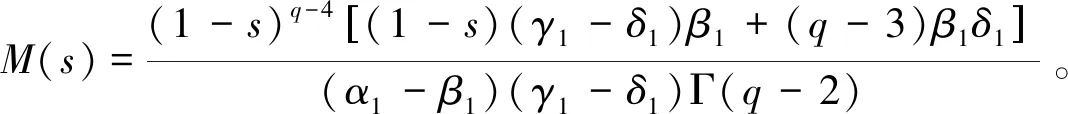
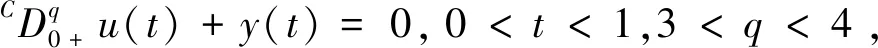
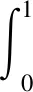
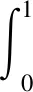
2 主要结果
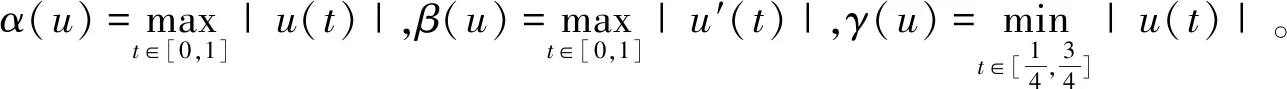
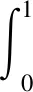
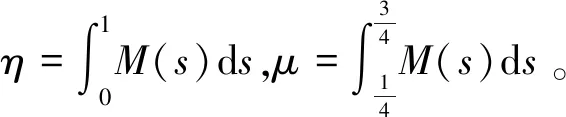

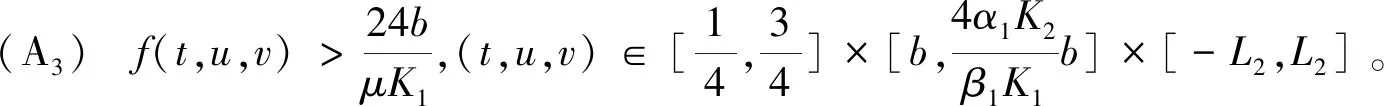
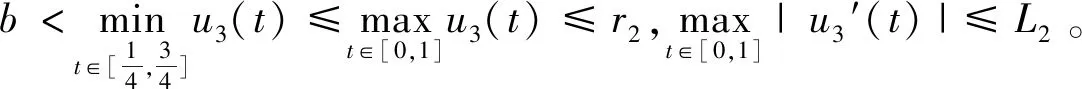
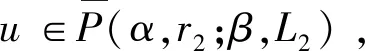
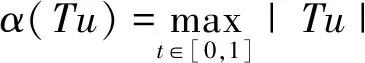

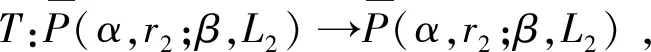
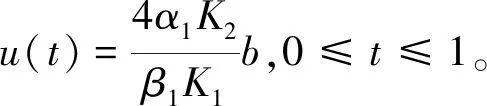
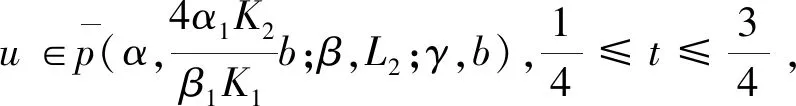
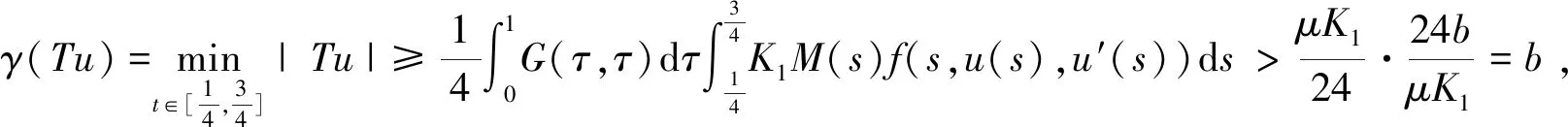
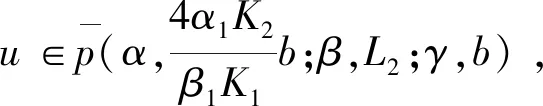
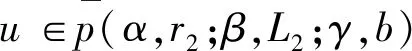
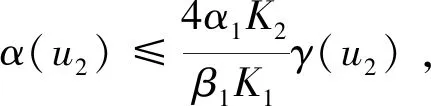
3 例子