一种含转动副间隙多连杆机构非线性动力学行为分析方法
,,
(山东科技大学 机械电子工程学院,山东 青岛 266590)
The planar multi-linkage mechanism is widely used in the mechanical industry for its simple manufacturing and high precision[1-2].However,when there is a clearance between the two components of the revolute joint,it will lead to the uncertainty of the motion of the mechanism,resulting in chaos and accuracy reduction of the mechanism[3].Therefore,it is necessary to study the nonlinear dynamic behavior of the multi-linkage mechanisms with clearance.
So far,many scholars have investigated the dynamic response of the multi-body mechanical systems with clearance.Based on the “contact-separation” model,Miedema et al.[4]divided the relative motion relationship on the revolute joint with clearance into three motion states,i.e.,contact,separation and collision,it analyzed the dynamic responses of the “contact-separation-collision” model.By considering the actual features of mechanism such as clearance,flexibility and friction,Chen et al.[5]developed a rigid-flexible model and studied the influence of the linkages flexibility and size of joint clearance on the dynamic behavior of the mechanism through automatic dynamic analysis of mechanical systems(ADAMS).With experimental platform,Erkaya et al.[6]investigated the effects of joint clearances on vibration and noise characteristics of mechanism and found that when the clearance value increases,the vibration and noise of the mechanism also become larger and exhibit nonlinear characteristics.By taking the influence of joint friction into account,Yaqubi et al.[7]analyzed the response of crank-slider mechanism with multi-clearance,and compared it with single clearance of crank-slider mechanism.Flores[8]conducted a continuous contacted force model based on the elastic Hertz theory,and analyzed the dynamic characteristics of crank-link mechanism.Yan et al.[9]used the classic impact method and the localized contact-deformation method to model contact-impact of clearance joints in the multi-body systems,and considered the effects of the gravity on the dynamic response.Zheng et al.[10]established a dynamic model of flexible multi-linkage mechanism with clearance and lubrication for ultra-precision presses,which considered the effect of revolute and spherical clearance joints,lubrication,and flexibility of crank shaft and linkage.Considering the clearance vector,Zhang et al.[11]built a collision-hinge model based on the dynamics modeling theory and analyzed the nonlinear characteristics of multi-linkage mechanism with clearances at high speed by solving the dynamic model.
Some scholars have studied the nonlinear dynamic behavior of the multi-body mechanical systems with clearance.Tang et al.[12]developed a four-bar linkage model considering clearance,and the effects of clearance value on dynamic responses were verified by Poincare map and bifurcation diagram.Muvengei et al.[13]studied the influence on dynamic behavior of clearance at different joints on the planar slider-crank mechanism without friction,and it has been found that the behavior of the mechanism changes from either periodic to chaotic,or chaotic to periodic depending on which joint has clearance.Rahmanian et al.[14]researched nonlinear dynamic behavior of a slider-crank mechanism with clearance.Bifurcation analysis has been studied with varying clearance sizes corresponding to two different crank angular velocities.Chen et al.[15]analyzed the parallel mechanism and the planar multi-linkage mechanism with clearance,which provided a reference for influence of clearance in different institutions.Wang et al.[16]described the separation process of collision by adapting a nonlinear spring damping model that conforms to the condition of contacting boundary,and discussed the nonlinear characteristics of mechanism with clearance joint.Olyaei et al.[17]studied the chaotic motion by using Poincaré map and fractal dimension of its strange attractor,and presented a control mechanism to control the chaotic motion based on the Pyragas method.From the literature view,it can be seen that there is a great need to investigate the dynamic behavior of multi-body mechanical systems with clearance,but the process of dynamic modeling is becoming more and more complex with the in-depth study of the mechanism with clearance.Therefore,it is imperative to find a simple and accurate analysis method to study the nonlinear dynamic behavior of multi-linkage mechanisms with clearance.
The main goal of this paper is to present a methodology to study the nonlinear dynamics behavior of a planar multi-DOFs complex mechanism with clearance and verify the effectiveness of the method by planar multi-linkage mechanism with clearance in revolute.Thus a method of forecasting the dynamic behavior of multi-linkage mechanism with clearance by analyzing the underactuated mechanism is proposed and the nonlinear dynamic behavior of 2 DOFs nine-bar mechanism with a revolute clearance is studied.The dynamic model of the underactuated mechanism is established and the motion characteristic of slider and driving torque of crank are studied.The chaos phenomenon existing in the mechanism is identified by phase diagrams,Poincaré portraits,and bifurcation diagrams.The effect of different clearance values and driving speeds on chaos are analyzed.
1 Establishment of dynamic model of mechanism with clearance
1.1 Model transformation of planar nine-bar mechanism with a revolute clearance
The mechanism consists of frame,Crank 1,Link 2,Link 3,Crank 4,Rocking-bar 6,Link 7,Link 8 and Slider 9.Link 5 is part of the frame.The model diagram of planar nine-bar mechanism with clearance is shown in Fig.1.In the model,the clearance revolute joint between Link 3 and Crank 4 is replaced by virtual massless link,which is called the clearance barr.The DOF of the mechanism has changed to 3,larger than the number of driving.The model is transformed from the multi-linkage mechanism with clearance to the underactuated mechanism.
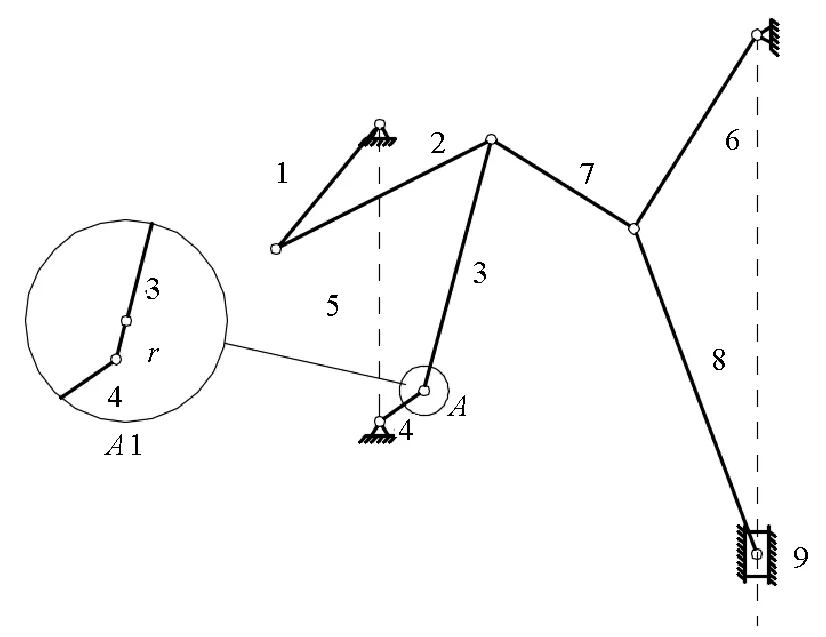
Fig.1 Model diagram of nine-bar linkage mechanism with a revolute clearance
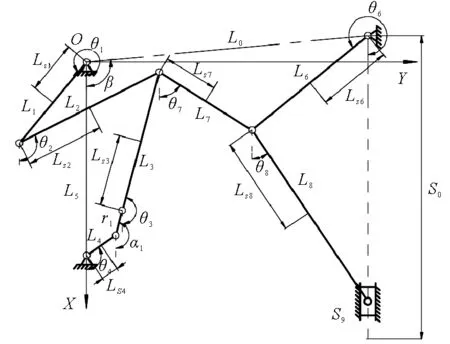
Fig.2 Coordinate system of the mechanism with a revolute clearance
1.2 Establishment of kinematics equation with a revolute clearance

For the transformed mechanism,the closed vector equation can be expressed as
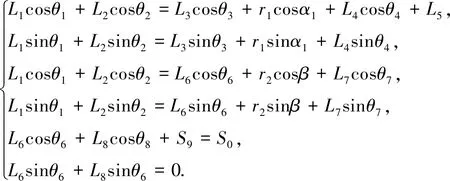
(1)
In the above model,the length of each bar and the motion law of the driving link are known,so six direction anglesθ2,θ3,θ5,θ6,θ7,θ8are unknown,and the clearance angleα1and the position of the sliderS9can be obtained by the above equation.
1.3 Establishment of dynamic equation with a revolute clearance
The dynamic model of the mechanism with clearance established by Lagrange equation is expressed as
(2)
Where,E,V,Qi,qirepresent kinetic energy,potential energy,general force and generalized coordinates respectively,andq1=θ1,q2=θ4,q3=α1.
The equation of the kinetic energy of the mechanism can be written as
(3)

When theOpoint is zero potential energy position and theXdirection is the gravitational direction,the potential energy of the mechanism can be written as
(4)
Considering the principle of virtual work,the relationship between generalized force and virtual displacement can be expressed as
δW=Q1δq1+Q2δq2+Q3δq3.
(5)
WhereQ1,Q2andQ3represent generalized force,respectively.
For the mechanism with clearance,the equation based on the virtual work principle is given by
(6)
According to Eq.(6),the generalized force of the non-conservative system can be written as
(7)
Where,M1andM2represent the driving torques of Crank 1 and Crank 4 respectively,andFris the resistance of slider.
1.4 Solution of the kinematic differential equation of the model
According to Eqs.(2),(3),(4) and (7),the Lagrange equation can be transformed as

(8)
Because the generalized force corresponding to the clearance bar is zero(Q3=0),the second-order nonlinear differential equations is derived forq3.Then
(9)
Eq.(9) can be expressed as
(10)
The fourth order Runge-Kutta is used to solve Eq.(11),and the value of the unknown quantityα1can be obtained.Then,theα1is brought into Eq.(2),and the displacement,velocity and acceleration of the slider can be deduced.
With the value ofα1being known,the expressions of two driving torques can be derived from Eq.(7) and Eq.(8).Then
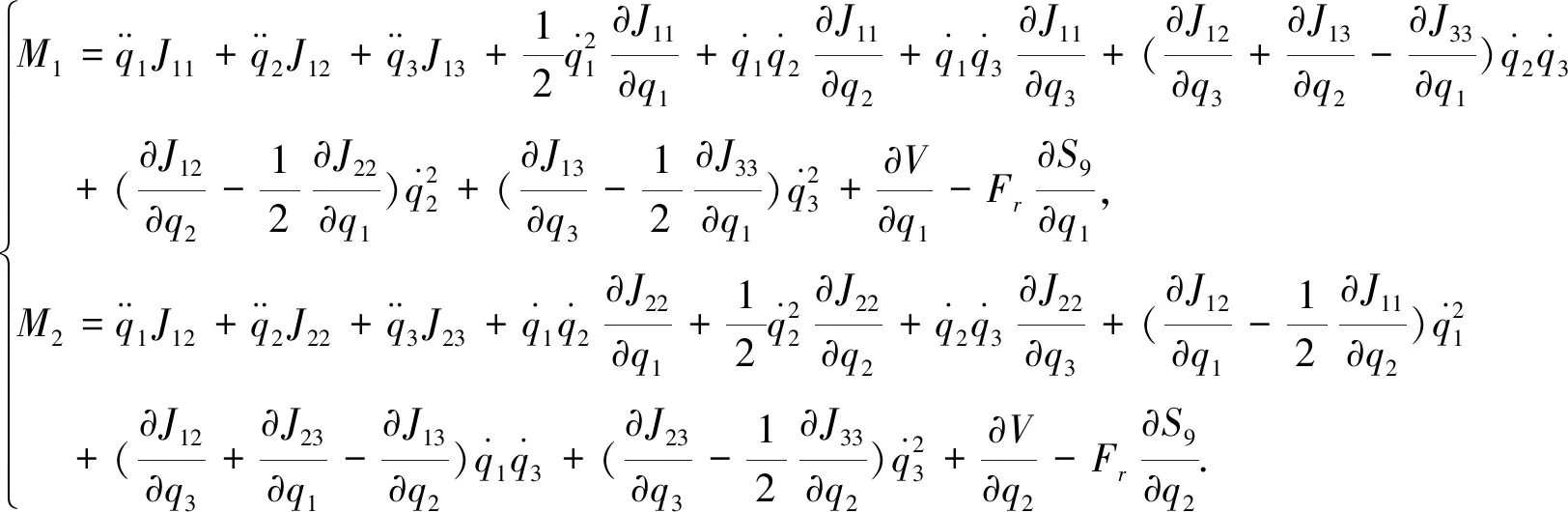
(11)
2 Nonlinear characteristics of planar nine-bar mechanism with a revolute clearance
2.1 Parameter setting of the mechanism with a revolute clearance
System parameters of the mechanism with clearance can be seen in Tab.1.
2.2 Chaos identification of mechanism with a revolute clearance
The speed of Crank 1 and Crank 4 are set to -π rad/s and π rad/s respectively,the length of the clearance bar is 0.15 mm.
The kinematic characteristic of slider are shown from Fig.3 to Fig.8.The displacement and displacement error are shown in Fig.3 and Fig.4 respectively.From Fig.3 and Fig.4,it can be seen that the displacement curve of the slider with a revolute clearance basically conforms to the displacement curve of the slider in the ideal state,and the maximum displacement error of the slider appears in the 1.232 s,and the error value is 7.806×10-5m.

Tab.1 Dimensions and mass properties for the 2 DOFs nine-bar mechanism
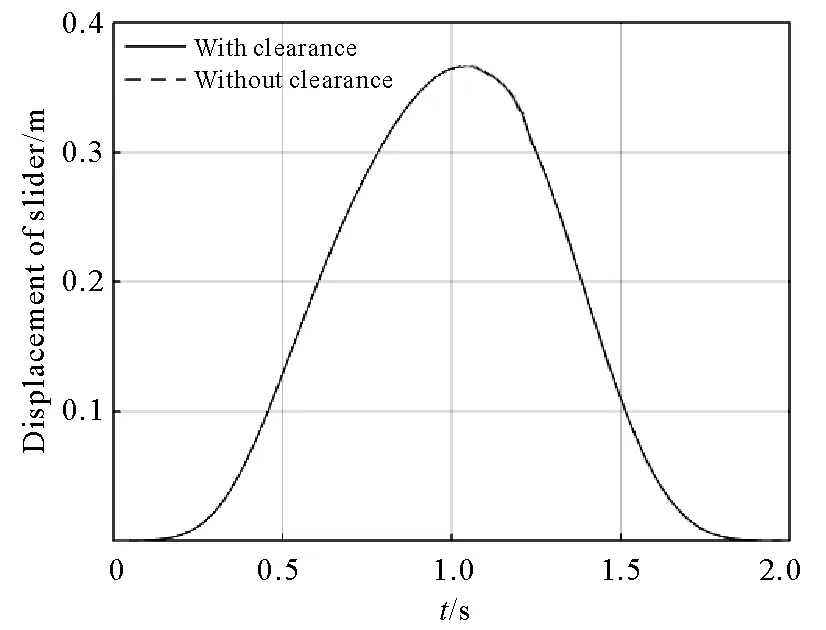
Fig.3 Displacement of slider

Fig.4 Displacement error of slider
The velocity and velocity error of the slider are shown in Fig.5 and Fig.6 respectively,and the results show that the clearance has a definite effect on the speed of the slider.The maximum velocity error of the slider appears in the 1.187 s,and the error value is 0.029 m/s.
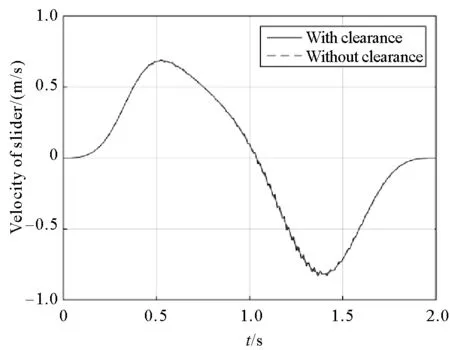
Fig.5 Velocity of slider
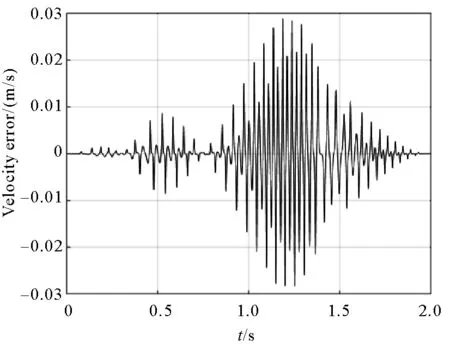
Fig.6 Velocity error of slider
The acceleration and acceleration error of the slider are shown in Fig.7 and Fig.8 respectively.From Fig.7 and Fig.8,it can be seen that the clearance has a more obvious influence on the acceleration,and that the acceleration curve fluctuates violently and a great peak occurs.The maximum acceleration error of the slider appears in the 1.152 s,and the error value is 8.684 m/s2.
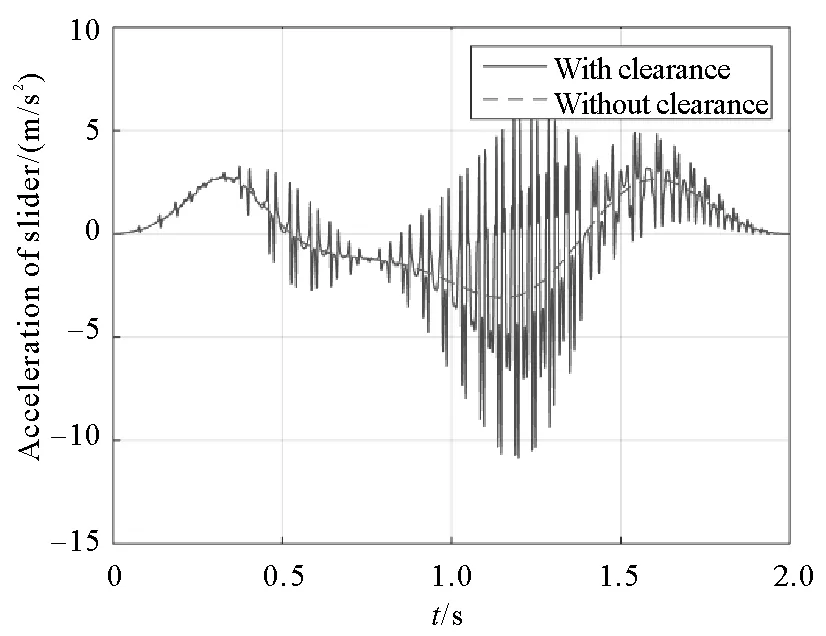
Fig.7 Acceleration of slider
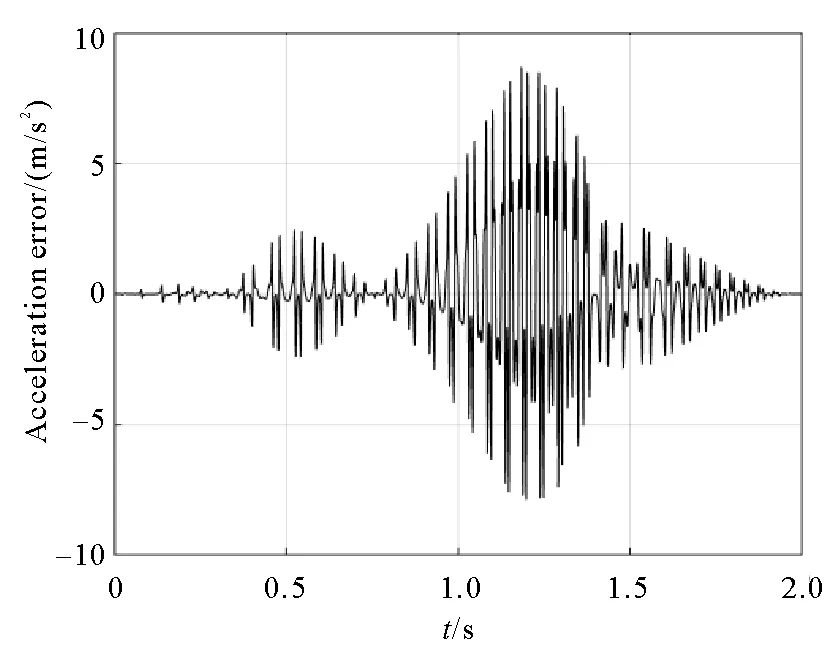
Fig.8 Acceleration error of slider
The driving torque curves of Crank 1 and Crank 4 are shown in Fig.9 (a) and 9 (b) respectively.From Fig.9,it can be seen that the driving torques of Crank 1 and Crank 4 generate peak values that are all at 0.528 s,the peak values are 43.394 N·m and 11.576 N·m respectively.The results show that the existence of clearance has a greater influence on the driving torque of the mechanism,which will cause obvious oscillation of the driving torque.

Fig.9 Driving torque of Crank
By drawing the phase diagrams and Poincaré portraits of the clearance bar,the chaotic phenomena in the motion of the mechanism are identified.
The phase diagram of the mechanism with clearance is shown in Fig.10.It can be seen from Fig.10 that the trajectory of the curve is not closed and in a mess,and the general trend of the phase diagram is more chaos,so the mechanism is in a chaotic state.
The Poincaré portraits is to cross the trajectory of the continuous motion with one plane,then the state of the motion can be judged succinctly according to the condition that the trajectory passes through the cross section.When the Poincaré cross section has only one isolated Poincaré mapping point or very few discrete points,the motion of the system is the periodic motion.When a continuous or discrete closed curve appears on the Poincaré cross section,the system does the quasi-periodic motion.When the Poincaré cross section has some patchy distribution of point set,the system is in chaotic state.
2.2.1 不同处理下基于DM的草地载畜量 不同处理下基于DM的草地载畜量变化与DM产量的变化相似(图1)。除6月施肥对杂类草DM载畜量(4.38羊单位/hm2)有显著促进作用外,其余各月施肥和补播处理对杂类草DM载畜量无促进效果。6月补播对禾本科(13.55羊单位/hm2)、豆科(7.68羊单位/hm2)和莎草科(5.68羊单位/hm2)DM载畜量的促进作用最明显。7月施肥处理下禾本科的DM载畜量(21.34羊单位/hm2)与CK差异显著(P<0.05);补播处理下禾本科(22.88羊单位/hm2)和豆科(11.48羊单位/hm2)DM载畜量显著高于施肥和CK(P<0.05)。
Poincaré portraits of the mechanism with clearance are shown in Fig.11.It can be seen from Fig.11 that the mapping points on the Poincaré cross section are distributed irregularly,indicating that the mechanism is in a chaotic state.

Fig.10 Phase diagram of the underactuated mechanism

Fig.11 Poincaré portraits of the underactuated mechanism
2.3 The effect of main parameters of the mechanism on the chaotic motions
2.3.1 Effect of clearance value on chaotic motion
To study the effect of clearance value on mechanism chaos,The driving speeds of Crank 1 and Crank 4 are fixed value -π rad/s and π rad/s respectively.The changes of the mechanism are observed by changing the length of the clearance bar.
The Poincaré portraits of the mechanism with different clearance values are shown in Fig.12.The Poincaré portraits of Fig.12(a),(b),(c) and (d) correspond to four sets of valuesr1 of 0.05,0.10,0.15 and 0.25 mm respectively.Whenr1 is 0.05 mm,the mapping points in the Poincaré portrait are chaotic and irregular,showing that the mechanism is already in chaos.With the increase of the length of the clearance bar,the distribution of Poincaré mapping points gradually decreases,but it is always in chaos.As shown in this model,even a small clearance will lead to chaos,and the intensity of chaos will decrease with the increase of the length of the clearance bar.
In the study of chaos,bifurcations can clearly reflect the effects of different variables on system behavior.So the bifurcation diagram of relative angular velocity versus clearance values is drawn to better realize the relationship between them.The lengths of the clearance bar ranging from 0.01 to 0.5 mm are selected to research bifurcation phenomena,as shown in Fig.13.According to the bifurcation diagram,the same conclusion can be obtained as the Poincaré portraits.Even a small clearance will lead to chaos,and the intensity of chaos will decrease with the increase of the length of the clearance bar.Through analysis,the reason for this phenomenon may be that the longer the gap bar is,the lower the swing frequency is.
2.3.2 Effect of driving speed of two cranks on chaotic motion
In analyzing the effect of the driving speed of two cranks on chaotic motion,the length of the clearance bar is set to the fixed value of 0.15 mm,and the changes of the mechanism are observed by changing the driving speed of two cranks.The unit of driving speed is ‘rad/s’,and it is omitted in the following text.

Fig.12 Poincaré portrait of the underactuated mechanism for different lengths of the clearance bar

Fig.13 Bifurcation diagram with varying clearance
The Poincaré portraits of the underactuated mechanism with different driving speeds are shown in Fig.14.The Poincaré portraits of Fig.14(a),(b),(c) and (d) correspond to four sets of different driving speedsω1=-0.5π,ω4=0.5π,ω1=-π,ω4=π,ω1=-1.5π,ω4=1.5π andω1=-2.5π,ω4=2.5π.As is shown in Fig.14(a),the mechanism is in a chaotic state.By comparing with other Poincaré portraits,it can be seen that the chaos is more obvious with the increase of the driving speed.
Bifurcation diagram with varying driving speeds is shown in Fig.15.The variation range of driving speeds of Crank 1 and Crank 4 are [-0.05π,-5π] and [0.05π,5π] respectively.From Fig.15,when the driving speed is small,the chaos of the mechanism is not so obvious.With the increase of the driving speed,the bifurcation diagram presents a divergence trend,and the chaotic phenomenon is more obvious.The main reason is that with the increase of the driving speed,the vibration of the mechanism becomes more intense.On the whole,the driving speed has great influence on the motion state of the mechanism.

Fig.14 Poincaré portrait of the mechanism with clearance for different driving speeds

Fig.15 Bifurcation diagram with varying driving speeds of two Cranks
3 Conclusions
In this paper,the nonlinear dynamic behavior of a planar 2 DOFs nine-bar mechanism with clearance is analyzed,the following conclusions can be drawn:
1) A method of forecasting the dynamic behavior of multi-linkage mechanism with clearance by analyzing the underactuated mechanism is proposed.And the dynamic equation of the mechanism with clearance is established according to the Lagrange equation.
2) The solution of the nonlinear dynamic model of the mechanism with clearance is realized by Runge-Kutta method.The kinematic characteristics of slider and the driving torque of the crank are analyzed.The nonlinear characteristics of the mechanism are obtained by the phase diagram and Poincaré portraits,and it is found that the clearance has an obvious effect on the stability of the mechanism and will cause chaos.
3) The effects of different clearance values and different driving speeds on the nonlinear characteristics of clearance mechanism are studied.Bifurcation diagrams with varying clearance values and driving speeds are drawn.The results show that with the increase of the length of the clearance bar,the chaos of the mechanism decreases gradually,and the chaotic phenomenon of the mechanism becomes more obvious,as the driving speed increases.
4) Through the above steps,the feasibility of the proposed method for analyzing the nonlinear characteristics of the multi-linkage mechanism with clearance is verified.

