结合重心坐标的泊松网格编辑算法

武 帅，黄庆学，李宏杰 ，王安红

(1.太原科技大学电子信息工程学院，太原 030024;2.太原理工大学，太原 030024)

在计算机动画中，网格变形日益完善，根据用户的需求对原始网格进行变形，比如给人物加上表情、给怪兽加上一系列动作等等，以此来达到用户的设计要求。网格变形最早采用自由变形技术，通过对原模型的顶点操作进行变形，但由于方法简单，变形时导致一些细节点丢失。基于多分辨率技术的网格编辑，通过对低分辨率网格进行编辑，还原到高分辨率的原模型上来实现变形，但只能有条件的保留模型细节点，变形时要对模型表面进行分离，使变形难度增加。基于微分域的网格编辑，将对顶点的操作转变为对微分属性的操作，通过点的映射关系，将绝对坐标转为相对应的微分坐标，较好的保留模型的局部细节特征，但模型的部分法向量并没有改变，从而导致变形后的模型看起来有点失真。重心坐标可用于将三角形内任意点表示为由三角形顶点组成的凸包组合，并用一种方便的方式无条件插在三角形顶点处。近年来重心坐标的思想已经扩展到平面中任意多边形和高维度的多面体，使网格的参数化、网格变形等应用有了新的解决方案。

2014年Niklas K, Matthias N, Konrad P[1]提出用于3D形状和纹理贴图的交互式建模框架，在微分变形的基础上结合几何画笔的思想，实现了局部缩放，但没有考虑梯度场方向的改变；2013年Chen C H, Tsai M H, Lin C I[2]提出的骨架驱动网格表面变形进行实时角色动画，通过构造包含输入表面网格的立方体单元格子，自动传播骨头平滑皮肤的重量，以驱动表面进行变形，但只能进行正数的加权计算；2011年Manson J, Li K, Schaefer S[3]提出的Gordon-Wixom坐标，在二维中引入任意闭合的重心坐标新结构，使用与边界曲线相切的距离定义正和平滑的权重函数来实现，采用多边形闭合解只能近似边界光滑；2010年S Sun, B Chen[4]提出的基于重心坐标的移动网格变形方法，首先计算要移动网格点的重心坐标，然后根据重心坐标插值边界点的位移来计算网格点的位移，计算量较大；2009年Xian C H, Lin H W, Gao S M[5]提出采用一种全自动的方法来生成一个包围网格模型的粗笼，自动生成的粗边界笼可以保持原网格模型的拓扑结构和主要几何特征，便于进行变形、细分、融合等操作，但对原始网格的要求较高；2016年杜正君、张慧[6]提出的体积图控制的近似刚性变形算法，采用体积图的近似刚性约束变形中的体积变化，克服了传统变形过程中不合理的体积变化，但算法需要多次迭代，并行计算的求解速度较慢；2015年张辉鑫[7]提出的基于广义重心坐标的三角网格变形方法，将原模型封闭到控制网格中，通过操作控制网格的变形带动原模型的变形，生成的是均匀的控制网格，没有考虑模型的简化与光滑处理；2015年张湘玉、李明、马希青[8]提出的基于细分的网格模型骨架驱动变形技术，通过建立骨架与控制网格、控制网格对应的细分曲面与变形区域间的关系，将对应细分曲面变化信息转化为网格模型泊松梯度场的改变，从而得到重建的网格模型，但由于模型表面拓扑结构的复杂，控制网格有时不能很好地贴合原模型形状，出现误差；2013年许斌、李忠科、吕培军[9]等提出的保持细节的网格曲面局部变形算法，依据用户对控制顶点的移动和网格表面几何特征，自动判断变形区域，将用户对控制顶点的编辑操作转为对模型泊松梯度场的操作，重建得到变形后的网格，但只考虑局部区域的变形，变形区域受限制。

通过以上比较，提出将自由变形技术与微分坐标结合起来，以重心坐标构造变形控制曲面，根据对重心坐标的编辑进行局部变换，通过局部变换得到变形后的梯度场方向，以此达到网格变形结果。该方法可以预先计算原网格模型的重心坐标，加快了并行计算，有效地克服了模型在变形过程中的变形问题，且能很好的保证变形的光滑。

1 重心坐标

重心坐标是指将原模型用一个空间网格包围，通过操作空间网格来实现变形，是用来描述原模型与空间网格间的几何关系。重心坐标常用的有均值坐标、调和坐标和格林坐标等。由于空间网格相对原模型有很少的顶点，通过对空间网格中的点进行操作，原网格上的对应位置就会发生改变。

Lipman[10]提出的格林坐标，利用偏微分方程理论与格林第三公式对拉普拉斯方程进行变化得到格林坐标。在三角网格中，包围网格P内P=(V,T)，V表示顶点集合，T表示三角形面集合，η表示点，Φi、Φj表示坐标函数，n(tj)表示面的外法线，则重心坐标为：

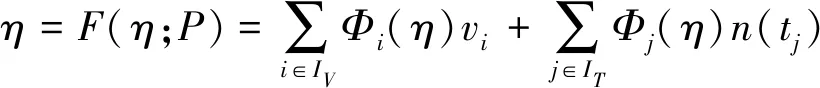
(1)

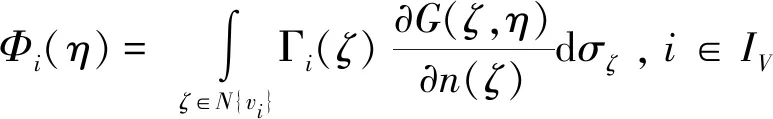
以重心坐标来构造待变形模型的控制网格，通过对控制网格的操纵实现原模型的任意变形。由于重心坐标具有自由变形技术的特点，因而本文提出的方法也具有自由变形技术的优势。

2 网格模型的泊松方程

泊松方程是一个偏微分方程

Δf=·wf|∂Ω=f*|∂Ω

(2)

2.1 三角网格梯度场

网格曲面上的分段线性标量场为f(η)=fi·Φi(η).

其中，fi是标量场在网格顶点η上的函数值，Φi是分段线性基函数。对于三角网格上的任意三角形Δvivjvk，任意一点η都可由其所在三角形的三个顶点线性插值得到：

f(η)=fi·Φi+fj·Φj+fk·Φk

(3)

则梯度为：

(4)

2.2 梯度场的散度

对梯度场求偏导得到三角网格梯度场的散度：

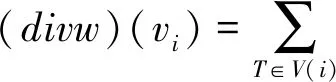
(5)

其中，V是顶点vi的一组三角形集，Bik表示定义在vi点的分段线性函数在三角形T上的梯度，A是三角形T的面积。

2.3 拉普拉斯算子

通过梯度场和散度算子，得到标量场f在顶点Vi的拉普拉斯算子，如图1所示，拉普拉斯算子为：

图1 拉普拉斯算子
Fig.1 Laplacian operator

对整个三角网格的拉普拉斯算子为

(7)

2.4 泊松方程求解

(8)

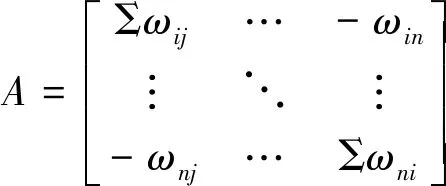
2.5 边界约束条件

泊松方程是一个微分方程，要求解微分方程，就需要有边界条件，如果一个顶点在网格中被确定，那么该顶点是约束顶点，也就是泊松方程的边界约束条件，如果一个顶点在网格中不被确定，那么该顶点是自由顶点。

对网格中的三个顶点不全是约束顶点的三角形集合进行局部旋转和缩放等操作，以三角网格的顶点(x,y,z)中每一维作为一个标量场，对不受约束的网格变形区域内每个三角形进行局部变换得到新的梯度场，然后计算散度，最后通过泊松方程重建网格模型，实现网格变形。

3 网格变形

三维模型的网格变形技术是在几何造型的框架下，通过引入一些权重来建立坐标之间的线性映射关系，从而根据用户的需求得到网格变形新模型。结合重心坐标的泊松网格编辑算法具体流程如图2所示，首先以原模型包围网格所确定的重心坐标生成控制网格，由于均值坐标的均值向量与三角面表面法向相同时，坐标值可能出现负数，不能满足局部特性；调和坐标包围网格的的复杂程度直接与计算过程的复杂性连接，进一步的发展较难；格林坐标是拉普拉斯方程的解，变形的光滑性高达C，这里主要采用格林坐标，一方面保证模型变形后的光滑自然，另一方面由于格林坐标中引入了法向信息，能很好的保持模型的细节特征，在大规模变形后使变形结果相对比较自然。然后任意改变包围网格，将对应重心坐标变化的信息转换为对应的标量场，估算网格模型每个顶点变形前后的局部旋转变换矩阵，求得每个顶点变形后的梯度场方向，对梯度场方向求导得到散度，最后通过求解系数矩阵进行网格重构得到变形模型。

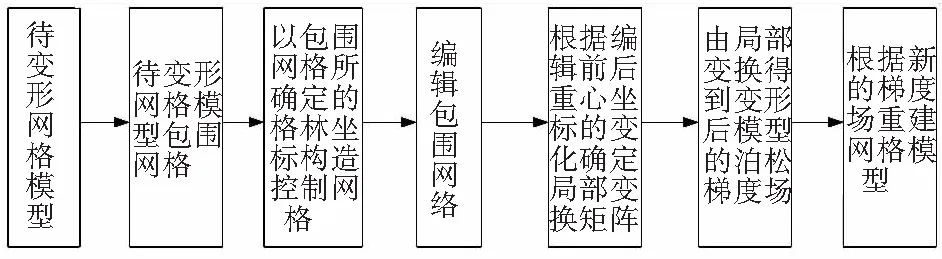
图2 流程示意图
Fig.2 Flow chart

3.1 确定重心坐标

构建包围网格是结合重心坐标进行泊松网格编辑的基础，采用简化模型来构造包围网格，然后对包围网格按照2.1节所示方法求取重心坐标得到控制网格，求出原网格模型每个顶点在包围网格上所对应的重心坐标位置。

3.2 确定局部变换矩阵

由于微分变形具有平移不变性，因而只考虑旋转变换和缩放变换。在原模型新顶点处定义局部标架，局部标架其中一个方向是边界点的法矢方向，另外两个方向在过边界点且以法矢方向为面法向量的切平面内，计算出变形前后控制网格顶点处的局部标架，从而确定唯一的旋转变换矩阵。得到三角形中心点变形前后的局部标架，根据局部标架法矢方向叉乘得到第一旋转轴，点乘得到第一旋转角度，局部标架以编辑前的位置为旋转中心，绕第一旋转轴和第一旋转角度得到中间标架，将中间标架与编辑后控制网格位置在切平面上投影向量叉乘得到第二旋转轴，点乘得到第二旋转角度。

根据编辑前后控制网格上三角面的周长确定缩放变换矩阵，三角网格中所有顶点的三个位置坐标分量构成三个标量场，按照2.2节所示方法求出每个标量场对应的梯度场。

如图3所示，任意的变形区域内，变形前后两关联位置vd和vd′，得到两个局部正交标架，其中的一个方向即为nd和nd′，另外的两个方向即为e1、e2和e1′、e2′.

图3 局部标架
Fig.3 Local frame

3.3 实现泊松变形

用户根据需求确定待变形区域的包围网格，以包围网格所确定的重心坐标生成控制网格，通过对包围网格的操作，将对应重心坐标变化的信息作为局部原点进行局部变换得到新的梯度场，代入泊松方程求最小二乘解得到变形的网格模型。

4 实验结果与分析

结合重心坐标的泊松网格编辑算法在Microsoft Visual Studio 2013平台上，编写基于MFC的图形界面，配有2.60GHz CPU，4.00GB内存，Windows 7系统的个人笔记本电脑。图4、图5和图6展示了采用本文算法对不同模型的变形效果。

a b

c

图4 立方体模型及变形
Fig.4 Cube model and deformation

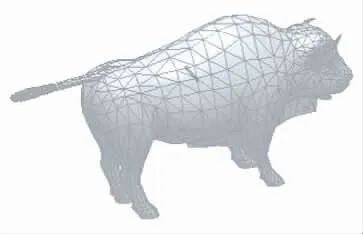
图4a是变形前立方体模型，图4b是本文算法进行扭曲变形的结果，图4c是本文算法进行弯曲变形的结果。图5a是变形前牛模型，图5b是本文算法对后腿进行变形的结果，图6a是变形前bunny模型，图6b是采用本文算法对bunny耳朵进行变形的结果。

a

b

图5 牛模型及变形
Fig.5 Cattle model and deformation

a

b

图6 bunny模型及变形
Fig.6 Bunny model and deformation

通过上述变形实验结果可以看出，本文算法充分体现了重心坐标作为变形控制网格进行任意拓扑的优势，无论对模型哪个部位进行变形，变形结果都保留很好的连续性，而且对模型的大尺度形变也能得到理想的编辑效果。图中的红色部分是编辑前后重心坐标构成的控制网格，白色部分是设置的固定区域。从变形结果可以看出，模型的细节特征在变形后都得到了很好的保持。

图7 传统泊松网格变形
Fig.7 Traditional Poisson mesh deformation

与传统的泊松网格变形算法相比较，针对图4b扭转变形结果，图7给出扭转变形的对比实验结果。可以看出，使用传统的泊松网格变形算法，扭转模型变形结果出现失真，有明显的棱角，而使用本文算法，模型扭转变形更自然，有很好的连续性。

5 结 论

要实现网格模型的保特征变形，不能直接用原网格的梯度场方向来重建变形后的网格模型，因而采用与重心坐标结合的泊松网格编辑方法，以包围网格来确定重心坐标进而得到控制网格，达到重新设置微分坐标方向的效果，对梯度场方向进行调整，最后重建出变形模型。该方法能够较好地保持网格模型的局部细节，使得变形后的模型更加光顺自然。尚有的缺陷是在网格进行局部旋转时，泊松变形将原来的非线性能量优化为线性融合，直观性不强。