最小二乘支持向量机的浓度读数模型及实现

范昌胜，刘泽照，郭 强，陈新庄

(1.陕西工商职业学院工程与建筑学院，西安 710119；2.西北工业大学理学院应用数学系，西安 710072)

近年来，随着工业化和城市化水平的提高，工业和生活污水中通常含有可溶酸性硫化物质。作为水污染控制工作中的基础性工作，硫化物含量的检测是水体环境监测的一个重要指标，其意义和作用也变得更加重要。现代数码照相技术的发展，使得采用仪器分析方法作为检测手段，溶液色度量化表示成为可能。这不仅可以大大改观以往以化学反应为显色原理的检测方法，而且避免了出现颜色的主观性判断、背景光线的影响以及不能用于定量及实现分析自动化等弊端。

根据朗伯-比耳定律(Beer-Lambert Law)可知，图像比色分析方法的原理：有色溶液的颜色深度(即有色溶液的色度)并不是简单的正比例于溶液的浓度关系，有色溶液的浓度与红(R)、绿(G)、蓝(B)三个颜色值和色调(H)和饱和度(S)值之间更多情况下呈现的是复杂的非线性关系[1,2]。由于图像色彩质量由R值、G值、B值3个数值有极大关系，于是讨论如何组合3个色彩值与浓度读数之间关系，建立相应的数学模型就显得尤为重要。现有文献使用比色法预测浓度使用的方法主要有偏最小二乘法、曲线拟合、多元线性拟合和支持向量回归等方法[3-5,13]。目前很多成熟的线性模型的数据拟合方法和理论，但对于实际问题的系统描述，这些方法往往会忽略数据本身固有的噪声，非稳定性和无序性等因素。支持向量机(Support Vector Machine, SVM)不仅在解决小样本、非线性及高维模式识别中表现出许多特有的优势，而且还可以克服局部最优问题[6]。最小二乘支持向量机(Least squares support vector machines ，LS-SVM)是在标准支持向量机基础上的扩展，它在保留支持向量机优秀特性的前提下，将支持向量机优化模型中的损失函数设定为最小二乘损失函数，并将不等式约束转化为等式约束．这样最小二乘支持向量机就将支持向量机的二次寻优问题转化成线性方程组的求解，极大地降低了求解的复杂性[7]。当前，最小二乘支持向量机方法比较成熟，被广泛应用于回归预测模型中[8，9]。

本文对溶液中二氧化硫的比色法测浓度问题，建立对应的浓度和读数拟合模型，采用最小二乘支持向量机(LSSVM)算法进行回归预测，改进图像比色法测定有色溶液浓度。文中针对比色法测试溶液浓度的问题，对于已有的颜色和浓度关系，建立支持向量机回归拟合模型，并用网格对其中所用参数进行寻优，通过实验数据进行了验证并简要说明了原理。当前，最小二乘支持向量机的研究比较成熟，已经形成了一套快速有效的实现算法。由于模型中有两个预置参数，文中给出了用网格法寻找最优参数的方法。同时对预测结果引入评价指标，并对给定的数据进行了实际验证，计算结果显示，LSSVM拟合结果与真实值比较吻合，与传统的线性拟合方法比较误差分析优势明显，是可以作为比色法使用的测量算法。同时对预测结果引入评价指标，并对给定的数据进行了实际验证。

1 构造最小二乘支持向量机(LSSVM)回归模型

假设样本集S={(xi,yi)|i=1,...,n}，其中xi∈Rp,p是解释变量个数，解释变量X∈Rp预测变量Y∈R.

支持向量机(SVM)模型思想为：如果训练样本在自身空间里是线性不可分的，那么就将输入空间X∈Rp.通过一个非线性映射φ(.)映射到一个特征空间φ(X)=φ(X1,X2,...,Xn)，然后在这个高维空间里进行线性拟合，即用一个超平面拟合样本点[9]。

本文采用函数f(x)=ωTφ(x)+b拟合数据点集，使拟合得到的值f(xi)与样本点值yi差值的平方最小，即求如下的优化问题：

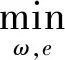
(1)

其中，γ为正规化参数，ek为误差，b为偏置。针对此优化问题构造拉格朗日函数进行优化求解，然后求出问题的对偶问题，由对偶理论的最优解满足KKT条件，得到矩阵方程(详细推导参考文献[10])：

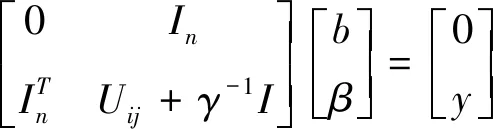
(2)

(3)

其中K(xi,xj)为核函数，本文采用径向基函数：

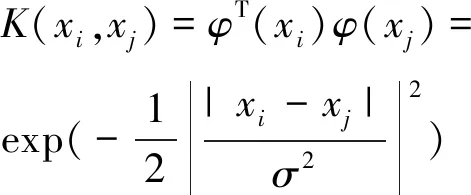
(4)

其中σ为尺度参数，它的取值决定了拟合函数的支持度和平滑性，σ的大小与待拟合的散乱数据点分布有关。

2 LSSVM回归模型求解

2.1 溶液的浓度、颜色读数及多次记录结果的原始数据关系

由于照片色彩易受外界因素影响的关系，选择一种能够排除外界因素影响照片色彩的拍照方式获取数据尤为重要。

1)在实验箱内拍照、采集溶液图像：将二氧化硫标准溶液依次加入到比色皿中，光照均匀，依次拍照采集溶液的图像并保存。这样获取得溶液图像RGB值稳定，能够量化表示溶液颜色。

2)数据组合统计方式：试验中使用上述方式，获取了7组25个不同浓度的二氧化硫溶液的颜色RGB值采样，经过取均值加工处理，见列表1.

表1 二氧化硫溶液浓度值与图像RGB均值表(N=25)
Tab.1 Potassium aluminum sulfate oncentration and image RGB mean value table(N=25)

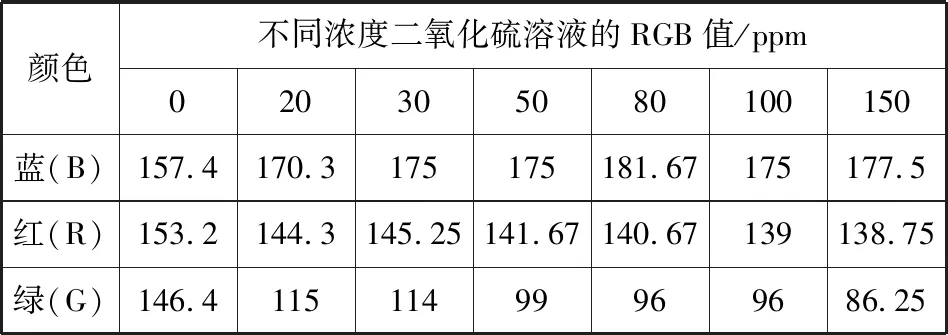
颜色不同浓度二氧化硫溶液的RGB值/ppm020305080100150蓝(B)157.4170.3175175181.67175177.5红(R)153.2144.3145.25141.67140.67139138.75绿(G)146.411511499969686.25

其中，ppm浓度(parts per million)表示用溶质质量占全部溶液质量的百万分比来表示的浓度，也称百万分比浓度，经常用于浓度非常小的场合下。如某溶液浓度为50 ppm，相当于是50 mg/L.

表2提供了简单的7种浓度的25个样本数据区间分布状况，每组浓度值对应的数据记录数为该组颜色采样的数据个数。

表2 溶液对应浓度值的数据记录数
Tab.2 The number of data records corresponding to the concentration value of the solution

浓度值/ppm020305080100150记录数5343334

2.2 LSSVM模型的拟合参数求解

针对最小二乘支持向量机回归模型的资料也非常多，如参考文献资料[11-14]。在提前给定正规化参数γ和尺度参数σ的情况下，将样本点、浓度显示数的表1数据带入优化模型，通过求解矩阵方程(2)可得到此模型的参数b和β，此过程称之为训练。然后上述LSSVM回归模型可以用来预测，对给定的待测值x=(X1,X2,...,Xt)，代入回归模型即可得到对应的预测值y(x)=(Y1,Y2,...,Yt).

根据经验，选择大约2/3进行训练是比较合理的，剩余的1/3用来验证回归结果。按照分层数据抽样和典型抽样结合的办法，每个浓度水平下留一条记录作为验证测试样本。对给定的25个样本按循序标号(1,2，…，25)，选取标号是(2，6，11，13，19，24)作为测试验证样本，其余的作为训练样本。

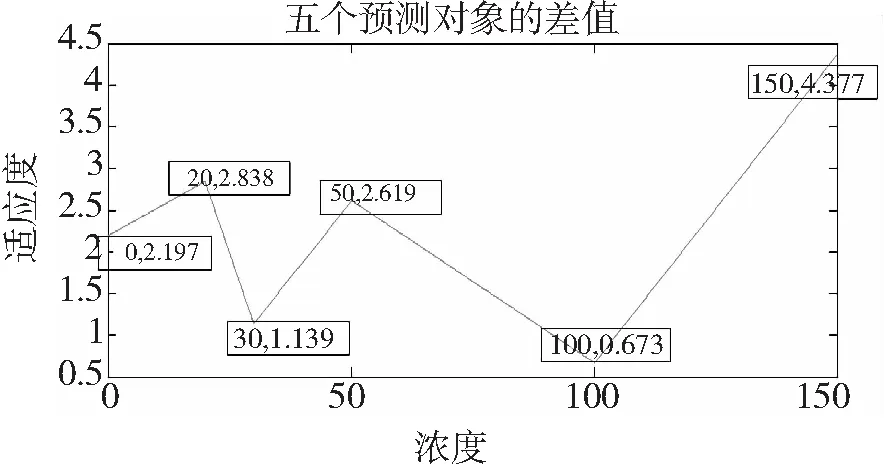
图1 在γ=10和σ2=0.5的预测结果
Fig.1 The results of the forecastγ=10andσ2=0.5

2.3 参数的优化

从上面的验证结果发现，设置不同的γ和σ的值，会得到不同的参数b和β值，预测的精准度会不同。实际上，不同的样本特征，最优的正规化参数γ和尺度参数σ的值是不同的。

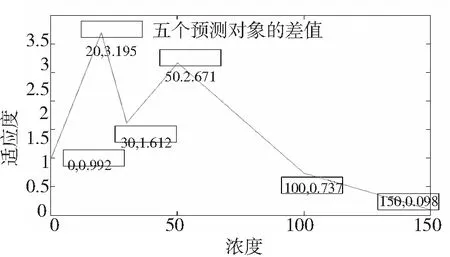
图2 是在γ=15和σ2=0.8的预测结果
Fig.2 The results of the forecastγ=15andσ2=0.8

本文采用网格法来选择最优的γ和σ：设γ∈[a,b]，σ∈[c,d]，这两个变量的可行域构成一个矩形区域，然后对此矩形区域进行网格划分，网格的每一个交点对应一组γ、σ值。

对给定的一组γ、σ值,使用LSSVM方法对待测试集中数据进行预测，将预测值与真实值的方差的倒数作为此组γ、σ的适应度。即：

(5)

网格上适应度最大的点，就是最优参数点。

为了减少搜索过程中的计算，可以先在大范围用大网格寻优，从结果中发现最优点所在的较小范围，然后再在网格划分重新寻优。多次这个操作，直到找到满意的最优点。

以上述表1数据为例，首先选择γ∈[1,20]，σ2∈[0.3,1.1]，构造网格meshgrid(1:1:20, 0.3:0.5:1.1)，然后使用LSSVM算法预测，网格每个点都会得到一个表示该值，如下图3所示：

图3中，发现在γ∈[10,12]，σ2∈[0.5,0.8]之间可能存在最大适应度的点。于是再次构造图4，网格meshgrid (10:0.2:12, 0.5:0.02:0.8)，找到最小适应度的点γ=10.4、σ2=0.6.

在这组值下，用LSSVM方法预测，依然选择序号是(2，6，11，13，19，24)的记录作为测试对象，结果如下：

图3γ∈[1,20]，σ2∈[0.3,1.1]，网格meshgrid(1:1:20, 0.3:0.5:1.1)
Fig.3γ∈[1,20]，σ2∈[0.3,1.1]，meshgrid(1:1:20, 0.3:0.5:1.1)

图4γ∈[10,12]，σ2∈[0.5,0.8]，网格meshgrid (10:0.2:12, 0.5:0.02:0.8)
Fig.4γ∈[10,12]，σ2∈[0.5,0.8], meshgrid (10:0.2:12, 0.5:0.02:0.8)

图5 序号是(2，6，11，13，19，24)的记录作为测试结果
Fig.5 The test results of serial records number 2,6,11,13,19,24

3 模型预测误差分析及评价

通常采用平均相对误差MRE、平均绝对误差MAE和均方根误差RMSE 三个性能指标评价预测模型，各自定义如下:

(6)

(7)

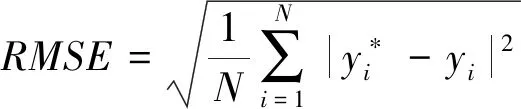
(8)

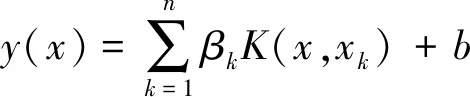
表3给出了所有的样本点(N=25)在三个性能指标评价下的预测值、差值、误差情况分析情况。

表3 所有的样本点(N=25)预测值、差值、误差情况分析表
Tab.3 All the sample points (N=25)prediction, difference, error analysis table

样本序号真实浓度值预测值差值平均相对误差MRE(单个贡献)平均绝对误差MAE(单个贡献)均方根误差RMSE(单个贡献)101.3221.3221.3221.3221.748201.0931.0931.0931.0931.195301.0371.0371.0371.0371.075401.0371.0371.0371.0371.075502.8232.8232.8232.8237.97262023.3413.3410.1673.34111.16272019.624-0.3760.0190.3760.14182024.2634.2630.2134.26318.17393026.564-3.4370.1153.43711.810103030.2770.2770.0090.2770.077113028.360-1.6400.0551.6402.688123029.510-0.4900.0160.4900.240135047.726-2.2740.0452.2745.173145053.9533.9530.0793.95315.623155054.3434.3430.0874.34318.860168078.861-1.1390.0141.1391.298178077.799-2.2010.0282.2014.843188082.2062.2060.0282.2064.8671910094.441-5.5590.0565.55930.9062010099.177-0.8230.0080.8230.67821100103.2653.2650.0333.26510.66022150145.859-4.1410.0284.14117.15123150144.670-5.3300.0365.33028.40724150148.147-1.8540.0121.8543.43525150149.537-0.4630.0030.4630.214

注释：上表中，测试验证样本数据用底纹深色进行标记。

最终得到LSSVM回归模型对应误差指标值，如表3.

对表3原始数据，论文所用方法与最小二乘线性拟合法等进行实验对比，给出对比数据和分析结果；在显著性水平为0.05的情况下，假设预测变量:三种颜色B,R,G值；因变量为浓度值，使用SPSS统计软件给出了表5误差分析表和表6 三元线性回归方程系数及标准误差。

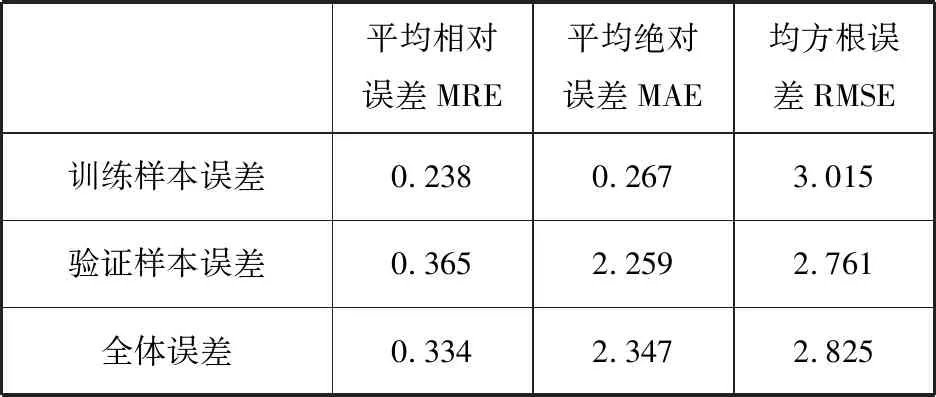
表4 LSSVM回归模型对应误差指标值
Tab.4 Index value of LSSVM regression model corresponding error

平均相对误差MRE平均绝对误差MAE均方根误差RMSE训练样本误差0.2380.2673.015验证样本误差0.3652.2592.761全体误差0.3342.3472.825

表5 所有的样本点(N=25)线性回归的方差分析
Tab.5 ANOVA analysis of linear regression for all sample points (N=25)

模型平方和df均方FSig.回归13 409.41434 469.8054.662.119残差2876.3003958.767总计16 285.7146

表6 所有的样本点(N=25)的线性回归系数及误差分析
Tab.6 Linear regression coefficients and error analysis of all sample points (N= 25)

模型非标准化系数标准系数B标准误差试用版tSig.常量492.2081 952.158.252.817R7.53016.230.727.464.674G-5.8884.551-2.261-1.294.286B-5.0634.147-.750-1.221.309

显然，样本的回归方差分析检验显著性并不明显，在浓度值与三种颜色B,R,G值的回归方程中， R、G、B三色系数分别是7.53、-5.888、-5.063，常数为492.208.经过计算，该线性回归模型的预测值与实际值的标准误差为4.165.于最小二乘的线性回归模型的标准误差明显大于本文给出的预测回归方法。计算结果表明，LSSVM在三种误差指标下都有很好的表现，是一种可靠有效的预测回归方法。

4 结束语

本文针对比色法测试二氧化硫溶液浓度的问题，对于已有的颜色和浓度关系，建立最小二乘支持向量机LSSVM回归拟合模型，并简要说明了原理。由于模型中有两个预置参数，本文给出了用网格法寻找最优参数的方法。同时对预测结果引入评价指标，并对给定的数据进行了实际验证，计算结果显示LSSVM拟合结果与真实值比较吻合，是可以作为比色法使用的测量算法。同时对预测误差分析，LSSVM在三种误差指标下都有很好的表现，是一种可靠有效的预测回归方法。与传统的线性拟合方法比较误差分析优势明显，是可以作为比色法使用的测量算法。由于LSSVM具有良好的推广特性，目前已成功地应用于函数逼近、信息融合、数据挖掘、金融预测等领域。