基于流固耦合方法的刷式密封刷丝变形及接触力特性的数值研究

刘璐园，张元桥，李 军

(西安交通大学 叶轮机械研究所， 西安 710049)

密封技术是提高透平机械性能的一项关键技术，不仅能够降低工质的泄漏损失、控制冷却气流的流动，还有利于提高整个系统的转子动力学稳定性[1]。刷式密封作为一种接触式动密封，其封严性能优良，泄漏量可以降低至传统非接触式密封的1/10[2]，因此在透平机械领域获得广泛应用。在设计安装过程中，刷丝束与转子面通常具有一定的干涉量，因此，在刷丝与转子表面间存在接触力。刷丝与转子表面的接触力直接影响着刷丝的变形程度、磨损速率以及刷丝束与转子表面的摩擦热效应。刷丝的变形量和磨损率决定了刷式密封的封严性能和使用寿命，而刷丝束与转子表面的摩擦热效应又会进一步加剧刷丝的磨损，同时在转子表面产生局部高温区，不利于转子的稳定运行。由此可见，对刷丝束与转子表面接触力的分析研究是提高刷式密封封严性能以及延长密封使用寿命的关键。

Modi[3]采用悬臂梁模型对单根刷丝底部与转子面的接触力进行计算，但模型中并未考虑刷丝与刷丝之间、刷丝与前后夹板之间的相互作用。Hendricks等[4]建立了一种更为全面的接触力分析模型，充分考虑了干涉量、气动力和压力载荷对刷丝底部接触力的影响，但模型中忽略了刷丝间的摩擦耦合。Crugington等[5]采用实验和数值两种方法研究了刷丝倾斜角对刷丝与转子面接触力的影响规律，但未考虑刷丝其他几何参数对接触力的影响。陈新春[6]等人采用线性悬臂梁和增强的拉格朗日法建立了单根刷丝与转子的接触力模型，分析了刷丝安装角、流体气动力以及刷丝与转子面干涉量对刷丝底部接触力的影响规律，但该模型仅考虑了单根刷丝，并未考虑刷丝之间、刷丝与前后夹板之间的相互耦合。李军等[7]采用悬臂梁理论分析研究了刷丝倾斜角、干涉量、转子偏心运动等因素对整圈刷丝与转子间接触力的影响，但该模型忽略了气动力以及刷丝内部的相互作用。

虽然很多学者对刷丝与转子表面接触力进行研究，但大多未考虑刷丝之间和刷丝与前后夹板之间的相互作用，关于流动与刷丝变形的耦合数值研究更是鲜有发表。因此，本文采用基于非线性Darcian多孔介质模型的三维Reynolds-Averaged Navier-Stokes (RANS)方程耦合Finite Element Method(FEM)的接触模型，建立了预测刷丝束与转子表面接触力以及刷丝变形的数值模型和计算方法，考虑了流体气动力、刷丝间摩擦力和刷丝与前后夹板间的相互作用。对比分析了单级刷式密封和两级刷式密封的刷丝变形量及其与转子面的法向接触力和摩擦力随压比的变化特性，探究了刷丝直径、刷丝倾斜角和干涉量对刷丝与转子表面接触力的影响规律。

1 数值方法

1.1 计算流程

图1给出了所提出的刷式密封刷丝变形和接触力特性的数值预测方法计算流程。采用基于非线性Darcian多孔介质模型的三维RANS方程耦合FEM的接触模型的方法，研究泄漏气流经过刷式密封时刷丝的变形及其与转子面的接触力。首先根据刷式密封的实际几何参数建立相应的刷式密封泄漏气流气动力的CFD模型和刷丝接触的FEM模型并生成初始网格，采用商用软件ANSYS CFX数值计算刷丝变形前气流对刷丝的气动力，然后将气动力作为载荷输入到FEM模型中并利用Mechanical APDL求解刷丝变形量及刷丝与转子的接触力，最后根据刷丝变形量生成新的网格并求解新的气动力、刷丝变形量和接触力。当刷丝变形量及刷丝与转子面的接触力变化小于0.1%时，则认为整个计算过程收敛。

1.2 刷式密封计算流体动力学模型

采用多孔介质模型模拟气流在刷丝束内部的泄漏流动，实质上就是在动量方程中增加粘性损失项和惯性损失项：

(1)

式中：Ai和Bi分别表示刷丝束多孔介质模型的粘性阻力系数矩阵和惯性阻力系数矩阵，μ是粘性系数，ρ是泄漏流体的密度，ui是流体速度。

根据Ergun方程[8-9]可以得到刷丝束多孔介质区域的粘性和惯性阻力系数：

Az=An=66.67(1-ε)2/(d2ε3)

(2)

As=0.4εAn

(3)

Bz=Bn=2.33(1-ε)/(dε3)

(4)

Bs=0

(5)

式中：Az和An为垂直于刷丝方向的粘性阻力系数，Bz和Bn为垂直于刷丝方向的惯性阻力系数，As和Bs分别为沿刷丝方向的粘性阻力系数和惯性阻力系数，d为刷丝直径，ε为刷丝束平均孔隙率。

以Bayley等[10]的实验测量单级刷式密封为研究对象，验证所采用的多孔介质模型对于计算刷丝束内部压力分布的有效性，从而间接证明该模型对于计算刷丝所受气动力的有效性。表1给出了密封结构的几何尺寸。由于刷式密封具有轴对称性，因此在转子圆周方向上选取1°弧段进行建模，采用ANSYS ICEM CFD软件生成密封的多块结构化网格，对壁面网格加密，当网格数目达到47万时可以获得网格无关解。图2给出了实验测量的单级刷式密封和作者设计的两级刷式密封的初始计算网格。

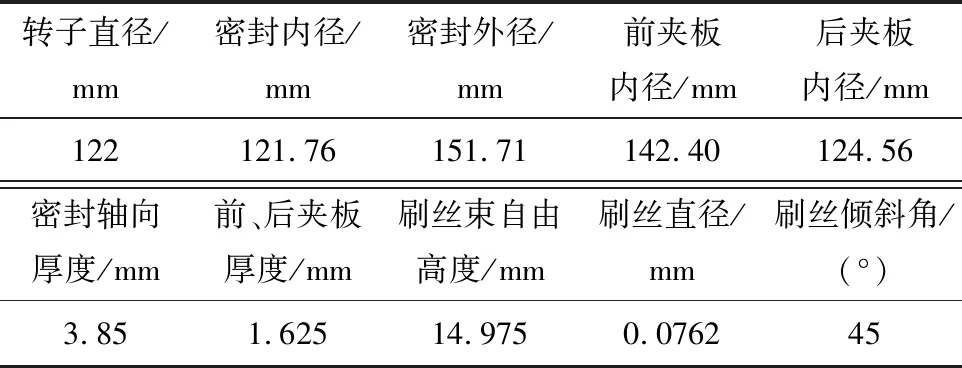
表1 刷式密封几何参数[10]

由于气流在刷丝束内部受到的流动阻力大，流速相对较低，因此在刷丝束以外和刷丝束内部区域分别采用SST两方程模型和层流模型模拟气流的泄漏流动。计算边界条件与实验工况保持一致，进出口压比为1.0～4.0，进口温度为20 ℃，出口静压为97 kPa，转子转速为0 r/min。

图3给出了实验测量的单级刷式密封在压比为2.0时，压力沿刷丝束顶端分布的实验和数值结果，可以看出，采用多孔介质模型计算得到的结果与实验值吻合良好，因此，采用多孔介质模型数值计算气流作用在刷丝束上的气动力是可行的。

1.3 刷式密封有限元接触模型

图4和图5分别为刷丝排布示意图和刷式密封有限元接触模型，将刷丝简化为交错排列的圆柱体，刷丝与转子面的接触处理为点面接触，刷丝与前后夹板的接触处理为线面接触，刷丝间的接触处理为平行梁接触。由于刷式密封具有轴对称性，在建立有限元接触模型时，可以在转子圆周方向上选取三列刷丝，在转子轴向则根据刷丝束厚度确定刷丝排数。

(6)

式中：w为刷丝束厚度，d为刷丝直径，δ为刷丝间隙，Nrow为刷丝束沿转子轴向的排数。

以Demiroglu等[11]接触力实验中的刷式密封作为研究对象，验证所采用的有限元接触模型对于计算刷丝与转子表面接触力的有效性。图6为刷丝束接触力随干涉量变化的实验和数值结果，由图可知，数值预测的接触力与实验值吻合良好，验证了所建立的刷式密封有限元接触模型的准确性和有效性。

以Bayley等[10]实验测量刷式密封建立有限元接触模型时，根据相应的材料特性，选取刷丝的弹性模量为206 GPa，泊松比为0.3，刷丝与转子之间、刷丝与前后夹板之间、刷丝与刷丝之间的摩擦系数分别为0.24、0.28、0.20[12]。采用所发展的考虑了泄漏流体气动力、刷丝间摩擦力和刷丝与前后夹板间的相互作用的刷式密封刷丝变形及接触力特性的预测模型开展刷丝束力学特性及其影响因素的研究。

2 计算结果分析

2.1 刷丝变形量

图7和图8分别给出了单级刷式密封和两级刷式密封各级在压比为2.0和4.0时的刷丝变形量。从图中可以看出，单级刷式密封和两级刷式密封中的上游级和下游级在泄漏工质气动力、刷丝束与转子面干涉量和前后夹板支撑力的共同作用下，围栏高度以下区域的刷丝排布更加紧密并向下游方向弯曲，末排刷丝与后夹板之间形成一个间隙。随着压比的升高，刷丝向下游的弯曲程度越大，末排刷丝与后夹板之间的间隙也越大。

对比单级刷式密封和两级刷式密封各级刷丝束的变形量可以看出，在相同压比条件下，单级刷式密封的刷丝变形量明显高于两级刷式密封中的上游级和下游级刷丝变形量，并且下游级的刷丝变形程度高于上游级刷丝变形程度。这是由于在相同压比条件下，单级刷式密封刷丝束承担总压降，而两级刷式密封中上游级和下游级分担了总压降，并且上游级压比分配小于下游级的压比分配，如图9所示。图10给出了作用在单级刷式密封刷丝束和两级刷式密封各级刷丝束上的轴向气动力随压比的变化情况，可以看出，作用在各级刷丝束上的轴向气动力随压比的升高而升高，并且作用在单级刷式密封刷丝束上的轴向作用力高于作用在两级刷式密封刷丝束上的作用力，作用在下游级刷丝束上的轴向作用力高于作用在上游级刷丝束上的轴向作用力，因此，在相同压比条件下，单级刷式密封的刷丝变形量高于两级刷式密封中上游级和下游级刷丝变形量，并且下游级的刷丝变形程度高于上游级刷丝变形程度。

2.2 刷丝束静压及流线分布

图11给出了刷丝变形前后单级刷式密封和两级刷式密封工质泄漏量随压比的变化情况，从图中可以看出，不论是刷丝变形前还是变形后，单级刷式密封和两级刷式密封的泄漏量均随压比的增大而增大。当刷丝束发生变形后，单级刷式密封和两级刷式密封的泄漏量均有所下降，并且单级刷式密封中泄漏量的减少程度大于两级刷式密封泄漏量的减少程度。这是由于单级刷式密封和两级刷式密封中的上游级和下游级在泄漏工质气动力、刷丝束与转子面干涉量和前后夹板支撑力的共同作用下被压紧，刷丝束厚度减小，孔隙率降低，刷丝束对泄漏工质的流动阻力增大，因此发生刷丝变形后两种刷式密封的泄漏量均有所下降，如图12(b)和图13所示，单级刷式密封刷丝变形后的刷丝束厚度小于两级刷式密封上游级和下游级刷丝变形后的刷丝束厚度。

图12为压比2.0时单级刷式密封刷丝变形前后静压等值线云图及流场分布情况，图12(b)中的白色虚线表示刷丝束初始位置。从图中可以看出，在泄漏工质气动力、刷丝束与转子面干涉量和前后夹板支撑力的共同作用下，单级刷式密封刷丝束变形明显，刷丝束整体被压紧，刷丝束厚度减小，孔隙率降低，对泄漏工质的流动阻力增大，最终导致密封的泄漏量降低。刷丝变形对刷丝束内部的静压分布几乎没有影响，变形前后静压下降均集中在围栏高度附近，在刷丝束内部存在径向及轴向压差；刷丝变形对刷丝束内部的流场分布有一定的影响，刷丝变形后末排刷丝与后夹板之间形成一个微小间隙，一部分泄漏气流流入末排刷丝与后夹板之间的间隙并沿着后夹板向转子径向流动，最终在围栏高度以下区域沿转子轴向偏转并流向下游区域。

2.3 刷丝与转子面接触力

图14给出了单级和两级刷式密封所受气动力随压比的变化情况。各级刷丝束所受沿转子轴向的气动力远高于沿转子径向和周向的气动力，三个方向上的气动力均随压比的增大而增大。此外，两级刷式密封各级刷丝束所受的三个方向的气动力都明显低于单级刷式密封，并且在两级刷式密封中，上游级所受的三个方向上的气动力明显低于下游级。

图15给出了单级刷式密封和两级刷式密封刷丝与转子面法向接触力和摩擦力随压比的变化情况。从图中可以看出，在单级刷式密封和两级刷式密封中，刷丝与转子的法向接触力和摩擦力均随压比的增大而近似呈线性增大。这一现象可以解释为当压比增大时，泄漏流体作用在各级刷丝上的沿转子径向的气动力增大，导致刷丝与转子面间的接触增强，接触力增大；另一方面是当压比增大时，作用在各级刷丝上的沿转子轴向的气动力增大，刷丝束发生轴向弯曲的同时排列更加紧密，刷丝与刷丝之间、刷丝与后夹板之间的接触增强，导致刷丝束的径向刚度增大，接触力增大。此外，两级刷式密封的各级刷丝与转子面的法向接触力和摩擦力都小于单级刷式密封，并且在两级刷式密封中，上游级刷丝与转子面的法向接触力和摩擦力要低于下游级刷丝与转子面的法向接触力和摩擦力。这是由于在两级刷式密封中，两级刷丝束分担了整个密封的压降，各级刷丝束承受的压降减小，气动力也相应减小，可以有效降低刷丝与转子面的接触力，减缓刷丝磨损和摩擦热效应。

2.4 刷丝束几何参数对接触力的影响

刷丝与转子面的接触力受刷丝直径、倾斜角和干涉量的影响，本节研究了刷丝直径、倾斜角和干涉量对刷丝接触力的影响规律。

在进行计算时，密封进出口压比均为2.0。图16至18分别给出了刷丝与转子面的法向接触力和摩擦力随刷丝直径、倾斜角和干涉量的变化情况。在数值模拟选取的参数范围内，刷丝与转子表面的法向接触力和摩擦力均随刷丝直径、倾斜角和干涉量的增大而增大，其中刷丝倾斜角为刷丝中心线与转子面的切向夹角。因此，为降低刷丝与转子面的接触力，减缓刷丝磨损速率，削弱刷丝和转子面的摩擦热效应，在进行刷式密封设计时，应充分考虑刷式密封几何参数对刷丝与转子面接触力的影响规律。对于典型的金属刷式密封，刷丝直径一般在0.06 mm到0.12 mm之间，刷丝倾斜角在30°到60°之间，刷丝束与转子面的干涉量一般小于0.3 mm。根据本文的计算结果，在上述范围内选取设计参数时，应尽量选取较小的刷丝直径、刷丝倾斜角和干涉量。

3 结论

采用CFD模型和FEM模型流固耦合的方法数值研究了单级和两级刷式密封在不同进出口压比下的刷丝变形量及刷丝束内部静压和流场分布，得到了刷丝与转子面的法向接触力和摩擦力随压比的变化规律。在此基础上，研究分析了刷丝直径、刷丝倾斜角和刷丝束与转子面干涉量对刷丝与转子表面接触力的影响。结论如下：

(1) 在单级和两级刷式密封中，刷丝变形量、刷丝与转子面的法向接触力和摩擦力均随压比的增大而增大。在压比较高时，刷式密封的磨损更加剧烈。

(2) 在相同压比条件下，两级刷式密封的刷丝变形量、刷丝与转子面的接触力明显低于单级刷式密封，并且上游级的刷丝变形量和接触力低于下游级。在相同压比条件下，两级刷式密封上游级和下游级刷丝与转子面的法向接触力较单级刷式密封分别可降低55%和32%。因此，采用多级刷式密封可以有效降低刷丝接触力，减缓刷丝磨损，延长刷式密封的使用寿命。

(3) 刷丝与转子表面的接触力随刷丝直径、刷丝倾斜角和刷丝与转子干涉量的增大而增大，为避免刷丝和转子面摩擦损伤以及摩擦热效应，在设计刷式密封时，应充分考虑刷丝束几何参数对刷丝与转子面接触力的影响。当刷丝直径小于0.08mm，干涉量小于0.1mm，刷丝倾斜角在30°～45°之间时，可有效降低刷丝与转子间的法向接触力和摩擦力。