铝合金焊接结构塑性变形及断裂失效预测方法

胡朝辉，杜 鹏，段利斌，周 聪,3，杜展鹏

（1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082；2.江苏大学 汽车与交通工程学院，江苏，镇江 212013；3.湖南大学 高性能复杂制造国家重点实验室，长沙 410082）

近年来，高质量的铝合金焊接结构件作为汽车上的关键零部件得到越来越广泛的应用。汽车前部铝合金焊接薄壁结构在碰撞过程中的变形和开裂失效关系到汽车碰撞能量的吸收和结构的完整性，进而影响汽车乘员区的生存空间和乘客安全。在汽车设计阶段需对性能进行准确、可靠的分析和评定，并对其变形和开裂力学行为有清楚的认识，从而为铝合金焊接结构的合理设计提供理论依据。

受焊接工艺的影响，铝合金焊接接头处材料的组织和成分变得与母材大不相同，焊缝和热影响区材料的力学性能发生了不均匀变化[1]。焊接接头力学性能的不均匀性会对焊接结构强度、耐撞性等性能产生很大的影响，同时也加大了焊接结构变形力学分析的复杂性。准确地获取焊缝、热影响区的材料性能数据，并在对焊接结构的性能进行有限元分析和评定时加以考虑，对分析得到真实可靠的结果至关重要。

关于焊接接头局部材料性能的获取，许多学者做了研究。NÈGRE等[2]直接截取微型尺寸平板样件进行拉伸试验，获得了不同子区材料的应力-应变关系。但焊接接头焊缝、热影响区等子区的几何尺寸太小，样件制作十分复杂。朱亮等[3]根据已有材料硬度与强度的关系，进行力学推导，利用X70管线钢焊接接头的硬度值分布，得到了其各子区的局部材料性能。该方法是以钢材硬度与强度的经验公式为基础，随着材料种类的不同会存在较大的误差。付磊等[4]结合数字图像相关技术（DIC）和硬度试验提出了一种识别接头子区材料幂指数硬化模型参数K、n的方法。ZHENG等[5]提出一种利用焊接接头拉伸试验结合有限元模拟迭代反求各子区材料性能的方法。该方法充分利用了焊接接头拉伸塑性变形集中的特点，通过拉伸试验获得的力-位移曲线提取出接头单个子区的材料性能数据，为焊接接头局部材料性能的获取提供了新的思路。

此外，铝合金材料的伸长率低于传统钢材，在变形过程中有较大的开裂倾向。铝合金薄壁结构的开裂属于典型的韧性断裂，汽车设计领域常用的极限塑性应变失效准则、成形极限图（FLD）等应用于铝合金薄壁结构的开裂预测具有很多局限[6]。断裂韧性J积分、裂纹阻力曲线等常被用作韧性材料宏观断裂准则，但它们与结构的几何形状和尺寸相关[7]。实际上，金属材料的韧性断裂行为与内部损伤的形核、生长及聚合存在紧密的联系。Gurson从细观损伤力学观点出发，提出了描述金属材料变形时内部损伤演化产生断裂的损伤力学模型。Tvergaard和Needleman对初始的Gurson损伤模型进行修正，进一步形成了GTN损伤模型。损伤力学模型以累积损伤变量临界值作为预测韧性裂纹生长的准则，更便于与有限元计算方法相结合。NEGRE等[2]采用GTN损伤模型对初始裂纹分别位于母材、焊缝、热影响区的3种铝合金激光焊接样件紧凑拉伸试验进行了有限元模拟，结果表明GTN损伤模型能够很好地模拟韧性裂纹的生长行为。但其模型中，只考虑了塑性变形早期材料较大夹杂粒子初始形核机制。

基于上述研究现状，采用GTN损伤模型模拟预测铝合金焊接接头的变形、损伤、断裂行为； 通过特殊样件进行单向拉伸试验，并结合有限元反求方法，获得铝合金焊接接头焊缝、热影响区局部的材料性能数据；建立铝合金焊接薄壁梁结构轴向压缩有限元模型，考虑焊接接头材料性能的不均匀性，预测铝合金焊接薄壁梁轴向压缩的变形开裂失效行为，最后通过试验对有限元模型进行了验证。

1 GTN损伤模型

GTN损伤模型描述了微观孔洞对材料塑性变形和断裂的影响。其屈服方程表达式为：

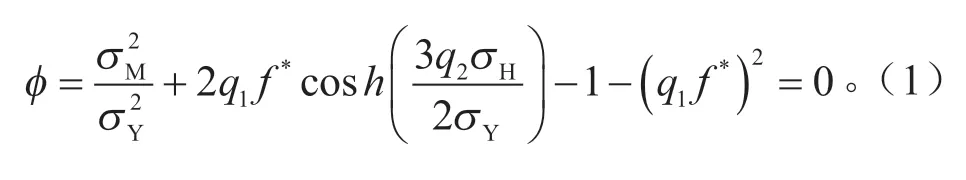
式中：σM为Mises等效应力；σY为孔洞周围基体材料流动应力；q1、q2为孔洞间的相互作用；σH为平均静水应力；f*为有效孔洞体积分数。当q1=q2=1时，GTN损伤模型退化为初始的Gurson损伤模型；f*=0时，材料没有损伤，GTN损伤模型退化为标准的Mises屈服函数。

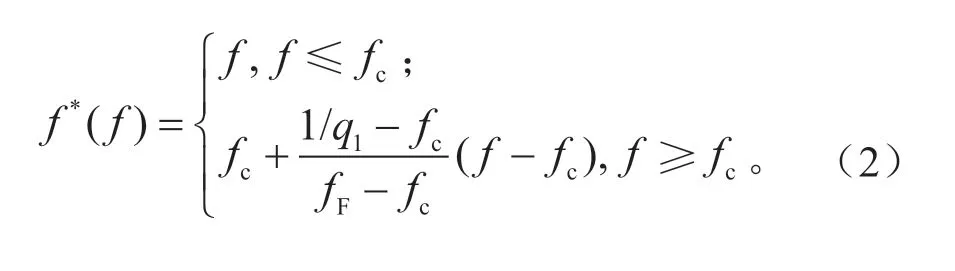
有效孔洞体积分数定义为：式中：f为孔洞体积分数；fc为临界孔洞体积分数，达到此值时，孔洞开始发生聚合；fF为断裂孔洞体积分数。

孔洞体积分数的演变包括孔洞形核和孔洞生长两部分。

孔洞生长建立在塑性变形基体材料不可压缩的基础上，其形式为：

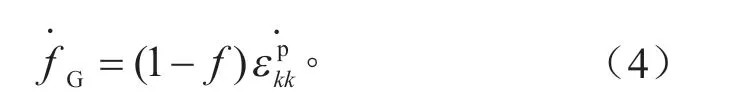
孔洞初始形核以初始孔洞体积分数f0表示。第二相粒子孔洞形核规律服从正态分布[17]，其形式为：

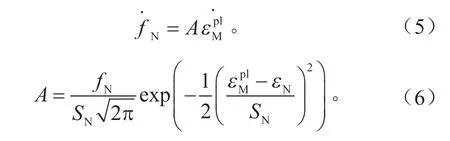
式中：fN为发生孔洞形核的第二相粒子体积分数；为孔洞形核平均塑性应变；SN为形核应变标准偏差1；ε为基体材料等效塑性应变。

2 铝合金焊接接头不均匀变形及材料性能

2.1 铝合金薄壁梁MIG焊接及拉伸样件制备

试验所用材料为6063-T5铝合金挤压型材。截面为长方形，尺寸为100 mm ×60 mm×1.8 mm。采用MIG焊接工艺进行对接拼焊，焊接设备为Lorch S5 RoboMIG XT焊机。使用Ar作为保护气体，焊丝牌号为ER5356，直径φ=1.2 mm。铝合金对接拼焊梁结构及焊缝外观形貌如图1所示，拼焊梁以焊缝为中心分为两段，每段长度为210 mm。

图1 焊缝表面形貌质量示意图

6063-T5铝合金母材拉伸样件从拼焊梁上部远离焊缝处，沿挤压方向截取，形状为标准“哑铃形”，尺寸依据GB/T 228.1—2010的规定。铝合金焊接接头截取3种不同类型样件，第1种为标准样件，尺寸依据GB/T 2651—2008的规定，第2种和第3种为特殊拉伸样件，并在焊缝中心和热影响区开设U形诱导槽，U形槽均位于长度方向中心线上，槽宽2 mm，槽深5 mm，槽末端圆角半径1 mm，具体如图2所示。加工好的4种不同类型拉伸试验样件如图3所示。

图2 两种特殊样件形状及尺寸示意图

图3 加工好的4种不同类型拉伸试验样件

2.2 母材材料性能

2.2.1 母材单向拉伸试验及结果

在30 kN的MTS万能材料试验机上对6063-T5铝合金母材标准样件进行准静态单向拉伸试验，拉伸速度为2 mm/min，拉伸直至样件断裂。得到母材力学性能见表1。

表16063-T5铝合金母材力学性能

母材样件拉伸断裂位置如图4所示，从图中可以很明显地看出样件在拉伸断裂前发生了一定程度的颈缩。

图4 母材拉伸试验样件宏观断口

2.2.2 母材损伤参数

建立拉伸试验有限元模型，使用16号全积分壳单元，网格尺寸为1 mm。为了模拟材料损伤断裂行为，使用材料模型为120号*MAT_GURSoN，材料输入参数为：弹性模量E=69 GPa，泊松比v=0.33，材料硬化行为以真实应力-塑性应变关系曲线模拟。

首先只调试GTN损伤模型中q1、q2和初始参数的值，以反映损伤导致材料的软化，直至仿真和试验得到力-位移曲线在断裂之前吻合。最后调试临界参数的值，以仿真和试验样件断裂起始时刻位移、断裂力大小一致为目标，对参数进行调试，最终得到合适的损伤参数。

适合6063-T5铝合金断裂模拟的GTN损伤参数见表2。本文统一取值q1=1.5，q2=1。

仿真和试验得到的力-位移曲线对比如图5所示。由图可知，承载力达到一定程度后迅速下降，说明样件在此时发生了断裂失效。试验样件刚发生断裂时对应的位移约为6.99 mm，对应的拉伸试验力大小约为4.7 kN。仿真样件刚发生断裂时对应的位移为6.70 mm，对应的拉伸力为4.81 kN，与试验值吻合得很好，验证了材料模型与损伤参数的正确性。

2.2.3 母材内部损伤演变过程分析

在断裂起始位置选取一网格单元，仿真得到总的孔洞体积分数、孔洞生长体积分数、孔洞形核体积分数演变过程如图6所示。

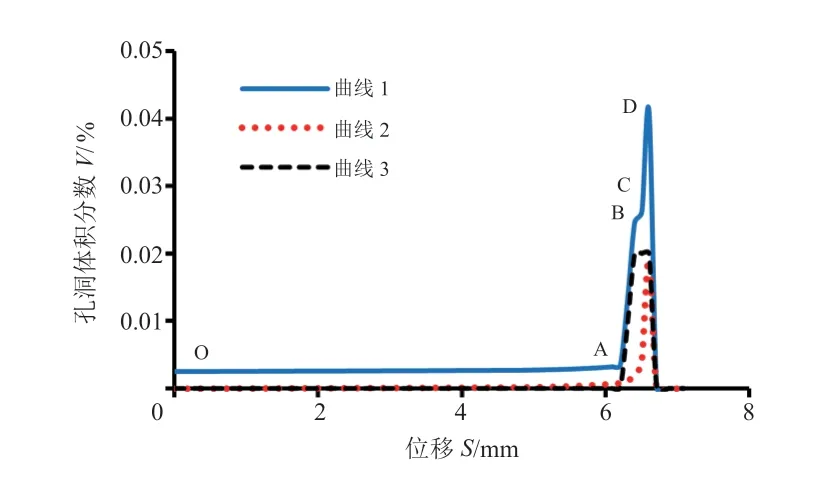
图6 孔洞体积分数随拉伸位移演变过程

曲线1上，oA段主要是初始孔洞体积分数，此时变形均匀，应力三轴度很小，孔洞几乎不生长；AB段等效塑性应变接近平均形核应变，第二相粒子形核，并且此时应力三轴度增大，孔洞开始生长；BC段第二相粒子形核完毕，应力三轴度继续增大，孔洞加速生长；CD段应力三轴度达到较高水平，孔洞高速生长。

孔洞生长随应力三轴度增大而加快。第二相粒子孔洞形核在等效塑性应变接近平均形核应变εN处发生，孔洞形核体积分数在总的孔洞体积分数中占大比重。在模拟材料颈缩之后快速断裂失效时，考虑第二相粒子的孔洞形核是十分必要的。

2.3 焊接接头局部材料性能

2.3.1 焊接接头拉伸不均匀变形行为

为了深入理解铝合金焊接接头的不均匀变形行为，对焊接接头标准样件进行拉伸试验。采用DH3817动静态应变测试系统及电阻应变计测量拉伸过程中焊接接头焊缝、热影响区及母材的变形量，同时，试验机记录拉伸力-位移曲线。焊接接头“哑铃形”样件应变计粘贴位置及测试过程如图7所示。

图7 焊接接头“哑铃形”样件应变计粘贴位置及测试过程

焊接接头“哑铃形”样件宏观断裂位置如图8所示。样件在距离焊缝约4 mm处的热影响区断裂，断口发生了明显的颈缩。

图8 焊接接头“哑铃形”样件宏观断裂位置

绘制焊接接头各子区小变形范围内应力-应变曲线，如图9所示。图中代号BM表示母材，WM表示焊缝，HAZ1和HAZ2表示距离焊缝较近处和较远处的热影响区，分别对应图7中应变计所粘贴测量的位置。

图9 应变计测得的各子区小变形应力-应变曲线

由图9可知，相同应力条件下，焊接接头各子区应变大小不同。拉伸变形过程中，HAZ1区塑性变形程度最大，最终颈缩和断裂也发生在此处，WM产生了一定塑性变形；HAZ2区产生塑性变形非常小，BM仅发生了弹性变形。

以产生0.2%塑性变形时的应力为材料屈服强度σ0.2，各子区材料屈服强度见表3。

表3 焊接接头子区材料屈服强度

WM、HAZ1、HAZ2屈服强度分别为母材屈服强度的65.7%、57.4%和79.2%。焊接接头拉伸变形不均匀与强度不均匀有很大关系，屈服强度小的子区塑性变形程度大。

采用Ramberg-osgood law公式对小变形范围应力-应变数据进行拟合。

Ramberg-osgood公式表达式为：

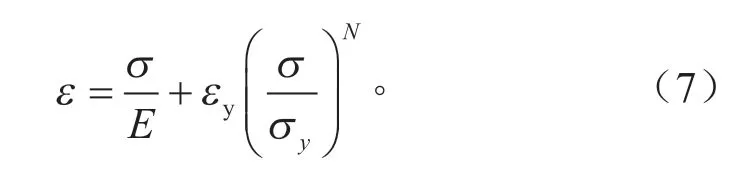
式中：σy、εy分别为初始屈服应力和屈服应变。拟合参数见表4。

表4 各子区小变形应力-应变拟合参数

2.3.2 焊缝及热影响区材料参数

为分别获得焊缝区、热影响区大变形范围真应力-应变曲线，对两种特殊焊接接头样件进行拉伸试验。

建立HAZ1区开U形槽样件拉伸试验有限元模型，网格模型根据实际划分为4个子区，单元尺寸为1 mm。

将HAZ1、HAZ2、焊缝小变形应力-应变拟合曲线作为对应子区材料性能初始输入，母材则输入3.2节中得到的材料参数。以仿真和试验得到力-位移响应一致为目标，单独修正HAZ1区大变形应力-应变曲线；以断裂起始时刻位移、断裂力一致为目标，调试得到HAZ1区GTN损伤模型参数。

HAZ1区开U形槽样件仿真与试验断裂位置对比如图10所示。仿真和试验断裂位置吻合一致，裂纹起始于U形槽，然后向样件中间扩展。仿真结果显示塑性应变集中在开U形槽一侧HAZ1区，焊缝对称侧未开槽HAZ1区有少量塑性变形。焊缝、母材、HAZ2区均处于弹性变形阶段。

图10 HAZ1区开U形槽样件仿真与试验断裂位置对比

HAZ1开槽样件仿真与试验力-位移曲线对比如图11所示。拉伸直到断裂起始位置仿真和试验力-位移曲线吻合很好，说明了HAZ1区材料应力-应变曲线和损伤参数的准确性。断裂起始之后，仿真拉伸力高于试验值，这是因为在仿真中将HAZ1材料视为均匀一致，而实际材料分布不均匀，裂纹沿着材料性能最弱的路径扩展。

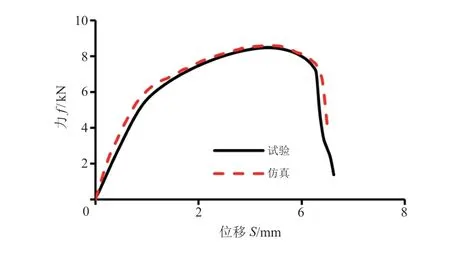
图11 HAZ1开槽样件仿真与试验力-位移曲线对比

采用相同的方法对焊缝区材料应力-应变曲线进行修正，并对焊缝区GTN损伤模型参数进行调试。

焊缝开U形槽样件，诱导槽使焊缝产生较大的塑性变形，试验初始裂纹首先出现在焊缝，如图12a所示，但焊接余高的存在阻止了裂纹在焊缝区的扩展；同时因为HAZ1区材料性能较弱，也发生了较大塑性变形，随后HAZ1区开始出现裂纹，如图12b所示；HAZ1区裂纹扩展，有与焊缝处裂纹汇合的趋势，如图12c所示。

焊缝开槽样件仿真与试验力-位移曲线对比如图13所示。拉伸直到断裂起始位置仿真和试验力-位移曲线吻合很好，断裂起始之后，仿真力高于试验值。焊缝区开槽样件，HAZ1区也产生了较大的塑性变形，相比HAZ1区开槽样件具有较大的断裂位移。

图12 焊缝开U形槽样件宏观断裂图

图13 焊缝开槽样件仿真与试验力-位移曲线对比

焊缝开U形槽样件仿真断裂起始位置如图14所示。仿真中裂纹在焊缝区起始和扩展，而实际样件裂纹起始于焊缝区，受到焊接余高的阻挡后又在材料性能较弱的HAZ1区形成裂纹。

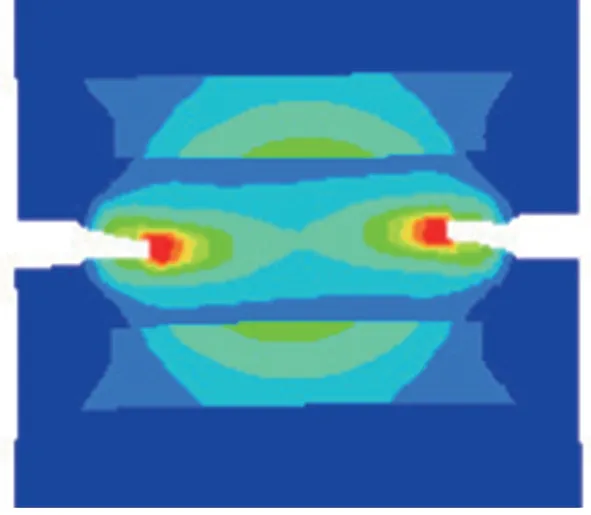
图14 焊缝开U形槽样件断裂起始位置

焊缝及热影响区修正后真实应力-应变关系曲线如图15所示。

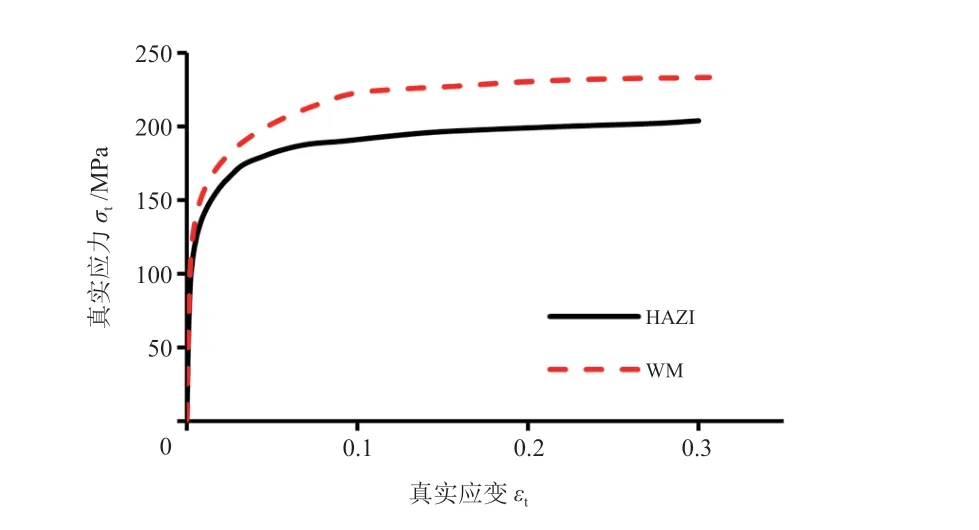
图15 焊缝及热影响区修正后真实应力-应变关系曲线

焊缝区及热影响区合适的GTN损伤模型参数见表5。

表5 焊缝及热影响区合适的GTN损伤模型参数

3 铝合金拼焊薄壁梁压缩变形有限元模拟及试验验证

铝合金拼焊薄壁梁轴向压缩试验在100 kN的型号为Instron 1346万能材料试验机上进行，如图16所示，压缩速度为5 mm/min。

图16 铝合金拼焊薄壁梁轴向压缩试验

建立铝合金拼焊薄壁梁结构轴向圧缩试验有限元模型，焊接接头每个子区划分到不同的组件，接头处网格尺寸为1 mm，如图17所示。

图17 铝合金拼焊薄壁梁结构轴向压缩试验有限元模型

薄壁梁上下两端面采用刚性盖板模拟压缩试验机对薄壁梁的压缩作用，下端保持固定，上端施加恒定的速度边界条件。母材、焊缝、热影响区材料输入修正的应力-应变曲线和损伤参数。

仿真和试验得到的压缩初始屈曲变形形态对比如图18所示。由图可知，屈曲失稳首先在焊接接头处热影响区发生，焊缝上下两侧热影响区都发生了失稳。由仿真和试验结果对比可知，仿真模型准确地预测了拼焊薄壁梁屈曲失稳发生的位置和变形形态。

图18 仿真和试验压缩初始屈曲变形形态对比

仿真和试验裂纹起始位置对比如图19所示。由图可知，试验中开裂现象起始于热影响区，然后向薄壁梁棱角处扩展，随后沿棱角纵向撕裂。仿真也很好地再现了这一过程，说明仿真模型能够准确预测拼焊薄壁梁的变形和开裂行为。

图19 仿真和试验裂纹起始位置对比

4 结论

本文通过特殊样件拉伸试验，结合有限元反求方法，详细表征了铝合金焊接接头局部材料性能，构建了从细观损伤力学角度预测焊接接头变形开裂现象的GTN损伤模型，对铝合金拼焊薄壁梁结构轴向压缩变形开裂进行了预测，并通过试验进行了验证，研究结果表明：

（1）利用焊接接头变形不均匀的特点，通过设置诱导结构进一步加剧塑性变形的集中性，然后通过简单拉伸试验结合有限元反求方法能够逐个获取焊接接头局部子区的材料参数。

（2）应用细观损伤力学模型，同时考虑初始粒子孔洞形核机制及第二相粒子孔洞形核机制，能够较好地预测铝合金焊接结构的损伤开裂行为。