基于拓扑优化的扭力梁式轿车后桥结构轻量化设计

汪 彬，陈光权，施卓奇，董卫平，Gaurav Kesireddy，张洪延

（1.浙江师范大学，浙江，金华 321004；2.托莱多大学，美国，托莱多 OH 43606）

随着汽车产业的发展，汽车工业在节能与环保方面面临巨大的挑战。日益严格的排放法规及汽车厂商之间激烈的竞争推动着汽车技术不断向更节能、环保、安全的方向发展[1-4]。大力发展汽车轻量化技术，在保障汽车安全性和其它基本性能的前提下，通过减轻汽车自身质量来实现节能减排一直是汽车生产厂商追求的目标[5-6]。

在轿车的新车型开发及轻量化设计过程中，后桥设计一直占据重要地位，其固有的特性直接影响着车辆的性能。新的后桥设计一般要求在有较高强度和刚度的基础上减轻质量[7-11]。

传统的后桥设计方法只是被动地重复分析产品结构性能，而不能主动地设计产品的结构形状和参数[12-15]。拓扑优化设计是在给定材料力学性能参数和指定的设计域内，得到满足约束条件又使目标函数最优的结构布局形式[16]。拓扑优化设计不需要知道具体的结构拓扑形态，是一种创新性的设计方法[17]。本研究在结构设计开始阶段采用拓扑优化设计，以获得较合理的初始结构方案，再对拓扑形态进行参数化设计，设计满足后桥强度和刚度要求的易成形的板材结构，不仅加快了后桥结构设计周期，节省了材料，而且在满足静、动态特性的前提下，达到轻量化的目的，对于车身后桥设计有很大的现实意义。

1 试验方法

本研究采用的具体研究方案如图1所示。首先将原后桥进行有限元建模及网格划分，分析加载载荷并加载，计算并分析原有后桥的模态及各种不同受力状态下的应力状态。然后设计出原后桥的拓扑域，加载原有后桥的工况进行拓扑结构优化计算，用所得拓扑结果导出CAD模型，并在CAD软件中进行重构。将重新设计好的后桥结构在有限元软件中再进行受力分析，和原有后桥的模态和应力应变情况进行对比分析，在满足各种工况并达到轻量化目的的条件下，获得最优的后桥结构。

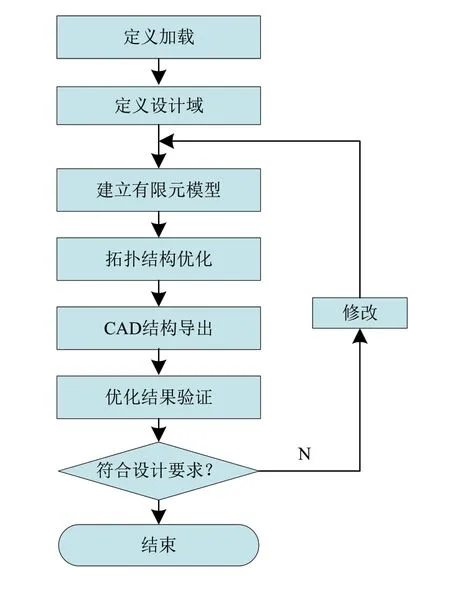
图1 后桥拓扑结构优化流程图

通过对原后桥进行模态及结构受力分析，分别计算了三阶模态及静载、启动或制动、侧翻状态下后桥的受力情况。在簧下空间的基础上，设定后桥拓扑优化模型，以后桥自重最小化为优化目标，以原后桥的受载情况为约束条件，建立设计域和非设计域，通过OptiStruct进行拓扑优化。利用OSSmooth工具进行了拓扑优化结果导出，在Solidworks三维软件中采用板材结构并在保持后桥安装部位不变的条件下进行重构。最后在有限元软件中进行应力分析以确认最终的优化结构受力是否满足要求，如不符合要求则返回重新进行拓扑结构优化，直至满足要求。

2 有限元模型的建立

2.1 几何模型及网格划分

扭力梁悬架作为汽车后桥的重要总成，既起承力作用又起导向作用。扭力梁悬架的强度能否满足实际汽车行驶中所遇各种工况的要求，将直接影响车辆的行驶安全性。原车的扭力梁结构及划分好的网格如图2所示，主要包括中间的横梁、纵臂、弹簧安装支座、减振器安装支座及轮毂安装支座。

在不干涉后桥周围构件的情况下，构建好的新后桥拓扑设计域及非设计域如图3所示，其中纵臂套筒、弹簧安装位置、减振器安装位置及轮毂安装位置为非设计域，其余部分为设计域。

图2 后桥结构有限元模型

图3 新后桥的拓扑设计域及非设计域

2.2 模态及各工况加载情况

模态分析不需要进行具体的加载，但需要定义边界条件。后桥结构和车身连接的部位主要是如图4所示的4个位置，即纵臂套筒1、弹簧安装位置2、减振器安装位置3及轮毂轴承安装法兰盘位置4。模态分析中原后桥及新设计的后桥约束定义了纵臂套筒1和弹簧安装位置2的全部6个自由度。

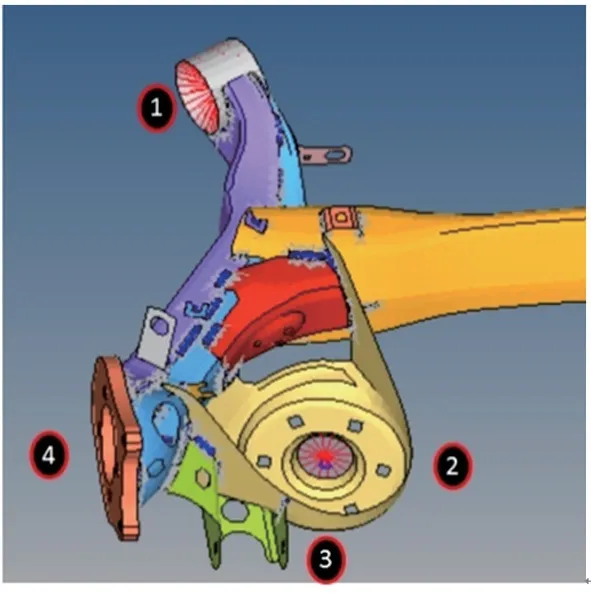
图4 后桥受力点位置示意图

对于扭力梁悬架强度问题，本研究主要考虑车辆在几种典型工况下极限载荷行驶时的结构强度，后桥结构受力简图如图5所示，FG、Fx、Fy、Fz分别为垂直下压力、纵向力、侧向力及垂向向上支撑力。扭力梁悬架的加载及约束形式较为复杂，特别是纵臂前端与车身相连的地方，该位置约束条件的不同将直接影响整个模型的仿真精确性。考虑到汽车行驶过程中，轮心处会存在垂直方向的轮跳输入和地面支持力输入，在仿真过程中也在轮心处加载。由于扭力梁悬架和车身相比，后者刚度更大，因此在仿真时采取对该连接点3个平动自由度全部约束住的边界条件，同样在扭力梁悬架与螺旋弹簧连接处也施加3个平动方向的约束。

图5 扭力梁后桥结构受力简图

对扭力梁后悬架进行受力分析，在静载、启动或制动及侧翻工况下的受力结果如下：在静载工况下，纵向力Fx为0，侧向力Fy为0，两侧垂直下压力最大值FG为0.5kG，k为动载系数取1.75，G为后桥最大静载荷，取6000 N，FG和Fz计算结果均为5100 N；在启动或制动工况下，侧向力Fy为0，纵向力Fx为0.5φFz，φ为纵滑附着系数，取0.8，垂向支撑力Fz为0.5mG，m取1.2，根据公式计算出垂向力Fz和纵向力Fx分别为3600 N和3456 N。当汽车发生侧翻时，纵向力Fx=0，侧向力Fy最大，外轮上的垂向支撑力Fz1和内轮上的垂向支撑力Fz2分别为：1920 N。式中，h为汽车质心高度486 mm，B为轮距2700 mm。内、外轮上的总侧向力Fy+μFz为6000 N，μ为侧滑附着系数，取1.0。

将分析所得的3种不同工况载荷加载到后桥上，通过分析计算后桥整体应力状况，并将最大应力与材料的屈服极限进行比较，对扭力梁悬架强度进行分析和评价。由于不同的载荷工况将得到不同的拓扑结构，本研究采用线性加权法，将静载、启动或制动及侧翻3种工况按照1∶1∶1进行加权，将多目标问题转化为单目标以获得各工况兼顾的拓扑结构。

3 结果分析

3.1 拓扑优化结果

通过对汽车后桥进行拓扑优化迭代计算，采用变密度方法，将连续体离散为有限元模型后，将每个单元内的密度指定为相同，以每个单元的密度为设计变量，以结构的体积百分比最小化为目标，考虑3种不同工况下的约束，使拓扑优化得到的结构质量最轻。最优的拓扑结构如图6所示。

图6 拓扑优化后的扭力梁悬架空间构架

通过OSSmooth工具将图6所示的拓扑优化结果导出，在考虑可加工性的基础上，采用板材结构，在Solidworks三维软件中进行CAD参数化设计，设计好的后桥结构如图7所示。将CAD重构的拓扑结构优化后桥在有限元软件中再次进行应力分析，以确认最终的优化结构受力是否满足要求。

图7 CAD重构的拓扑结构优化后桥

3.2 模态与减重分析

对 Hypermesh 中已建好的扭力梁总成有限元模型，施加纵臂套筒和弹簧安装位置的固定约束，不添加任何载荷。创建相应约束条件计算其模态，设置输出频率范围为 0～300 Hz。各阶频率及模态云图如图8所示。

图8 扭力梁后桥前三阶模态

由图可知，原车后桥的一阶模态为129.11 Hz，而拓扑优化后的后桥一阶模态为109.63 Hz，大幅小于原车的模态值，同时二阶及三阶模态值也均小于原车值。

同时，在保证受力部件不变的情况下，即套筒、弹簧安装位置、减振器安装位置及轮毂安装位置和尺寸保持不变，在保证与原车车身装配的前提下，拓扑优化后的结构采用板材重构后桥。结果显示，原后桥质量由19.06 kg减少到拓扑结构优化后的17.67 kg，减重7.29%。

3.3 各工况下的结构强度分析

图9为不同工况下原后桥和优化后的后桥应力应变云图。由图可知，3种工况下，原后桥及优化后的后桥出现最大应力值的部位都位于横梁与纵臂连接处，且弹簧和减振器安装位置所受应力较大。

将原后桥和重构后的板材结构后桥在Hyperworks软件中进行应力分析，得到的原后桥和优化后的后桥各工况下最大米塞斯应力对比结果见表1。由表1可知，在静载工况下，优化后的后桥最大米塞斯应力较原后桥稍大，但启动或制动工况、侧翻工况下的应力值都比原后桥小。新设计的后桥在各工况的极限下均未达到材料的许用应力值，满足要求。

图9 不同工况下原后桥及优化后的后桥应力应变云图

表1 原后桥和优化后的后桥各工况下最大米塞斯应力

4 结论

通过拓扑结构优化设计不但使后桥结构的设计时间缩短，节约了材料，同时在符合静、动态特性要求的前提下，实现了轻量化的目标，对改良后桥结构的设计方面具有指导意义。主要研究结果如下：

（1）根据原后桥的技术指标和参数要求，设定拓扑优化模型，以后桥自重最小化为优化目标，以原后桥的受载情况为约束条件，在簧下空间的基础上，建立了优化设计域和非设计域，通过OptiStruct进行拓扑优化。

（2）利用OSSmooth工具进行了拓扑优化结果导出，在Solidworks三维软件中进行了CAD图纸的修正处理以适合批量化生产，并在有限元软件中进行了应力分析以确认最终的优化结构受力满足要求。根据尺寸优化的最终结果，获得了最佳的拓扑结构优化后桥。