延性剪切薄板钢支撑的简化滞回分析模型

王枭迪，孙国华,2，包 成

（1.苏州科技大学 土木工程学院，江苏 苏州 215011；2.苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

Giannuzzi博士[1]提出了一种新型延性剪切板支撑（Braced Ductile Shear Panel，BDSP），这种抗侧力构件滞回曲线饱满、耗能优良，但震后塑性残余变形较大，不利于震后修复。本文在该支撑的基础上，将延性剪切厚板替换为易屈曲的薄钢板，形成延性剪切薄板（Ductile Thin Shear Panel，DTSP）钢支撑。其目的是充分利用剪切薄板的屈曲特性，期望DTSP支撑在低周往复荷载作用下的滞回曲线趋于捏缩。本文所提出的DTSP钢支撑具有水平承载力高、抗侧刚度大、变形能力优良、滞回曲线捏缩等特点。将该支撑用于自复位抗侧力构件的耗能装置时，能有效降低构件所需的复位力。DTSP支撑作为一种新型抗侧力构件，在未来自复位结构的抗震设计中具有广泛的前景。目前，虽然采用实体单元能较好地模拟DTSP支撑的滞回性能，但因单元量过多、建模过程复杂、剪切薄板易屈曲等原因，均会导致模拟计算过程中耗时过长及不易收敛。基于此，提出DTSP钢支撑构件的宏观简化模型，它可用于工程分析及设计，在工程应用中显得尤为必要。

目前，大量学者对钢板剪力墙的简化分析进行了大量研究[2-7]，但尚未有学者对DTSP钢支撑的简化模型开展研究工作。本文对不同高厚比、不同剪切板尺寸的DTSP钢支撑进行了系统研究，在明晰其力学性能的基础上，提出了一种适用于DTSP钢支撑的交叉杆简化模型（Cross-Braced Simplified Model，CBSM），并从滞回曲线、累积滞回耗能等方面验证了CBSM的精确性。

1 有限元模型的建立和验证

文献[8]进行了8个1∶3缩尺的BDSP支撑的低周往复加载试验。为验证有限元模拟的准确性，对试件BDSP-1进行有限元模拟验证，试件BDSP-1的几何尺寸见图1。采用ANSYS程序建立BDSP-1试件的有限元模型，其周边加载装置、板铰、斜撑、边缘构件均选用Solid185单元模拟，屈服应力取312 MPa，弹性模量取2.06×105MPa。中间部位的剪切钢板采用Shell181单元，屈服应力取290.5 MPa，弹性模量取2.04×105MPa，引入一阶屈曲模态作为剪切钢板的初始缺陷，缺陷幅值取剪切钢板高度的1/1 000。有限元模型见图2。

图3所示为试件BDSP-1的试验结果与有限元分析的滞回曲线对比。由图3可知，试件BDSP-1有限元模拟的滞回曲线与试验结果吻合良好，误差较小。这充分说明ANSYS有限元程序能较好地模拟BDSP支撑的滞回性能。

图1 试件BDSP-1的几何尺寸

图2 试件BDSP-1的有限元模型

图3 滞回曲线对比

2 DTSP钢支撑的滞回性能

2.1 DTSP钢支撑的试件设计

由于DTSP钢支撑的跨度、高度、剪切钢板厚度、剪切钢板尺寸等参数均对其滞回性能有显著影响。考虑上述参数设计了12个DTSP钢支撑的试件，见表1所列。为明晰延性剪切薄板支撑的滞回性能，消除钢梁、钢柱的影响，钢梁、钢柱与斜撑之间均采用铰接销轴连接。DTSP试件的几何尺寸见图4。其中，试件层高为3 600 mm，钢梁跨度为 6 000 mm，剪切板厚 tw，剪切板长 l，剪切板高 h，高厚比 λ=h/tw，剪切板尺寸系数α=l/L。所有试件的钢梁、钢柱截面均为□300 mm×20 mm，斜撑截面为H294 mm×200 mm×8 mm×12 mm，剪切薄板与斜撑刚接，且剪切钢板周边的翼缘采用尺寸为200 mm×12 mm的钢板约束。

图4 DTSP钢支撑的几何尺寸

表1 试件参数

采用ANSYS程序建立了DTSP钢支撑的微观有限元模型。试件SN1的有限元模型见图5。其中，钢梁、钢柱、斜撑及边缘钢板均采用Solid185单元模拟，剪切薄板采用Shell181单元模拟。钢材选择理想弹塑性模型（见图6），采用Mises屈服准则考虑钢材的包辛格效应。钢材的初始弹性模量E=2.06×105MPa，屈服强度fy=235 MPa，泊松比ν=0.3。采用一阶屈曲模态的1/1 000作为剪切钢板的初始缺陷。下部钢梁底部施加固接约束，钢梁、钢柱与斜撑均施加面外约束，销轴部分采用接触模拟。

全程采用位移控制加载，水平位移施加于上部钢梁，每级荷载循环1次，加载制度见图7。

2.2 DTSP钢支撑的滞回性能

图5 试件SN1的有限元模型

图6 钢材的本构模型

图7 加载制度

对DTSP钢支撑试件进行了滞回性能分析，以试件SN1为例。图8所示为试件SN1基于精细化有限元模型分析的滞回曲线。由图8可知，试件SN1的滞回曲线呈明显的捏缩特征，与Giannuzzi博士提出的延性剪切板试件的滞回曲线差异巨大。总体上，通过优化剪切钢板厚度可获得更为捏缩的滞回曲线，能实现最初设计目标，即当将其用于自复位构件中的耗能部件时可提供较大承载力和刚度，降低用于实现复位所需的回复力。SN1试件经历了弹性、弹塑性、塑性三个阶段。在层间位移角达到0.5%时，试件SN1显著屈服，其水平承载力为518 kN。

为确保DTSP钢支撑简化模型提出的合理性，分别提取了其微观有限元模型中支撑的轴力，其提取位置见图5。图9中给出试件SN1在层间位移角达到0.5%时的应力云图。由图9可知，在层间位移角达到0.5%时，斜撑截面一、截面二的水平内力分别为444.4 kN和61.7 kN，两者之和为506.1 kN。截面一与截面二所对应的水平内力存在显著差异，截面一的斜撑受拉，截面二的斜撑受压，受压斜撑的承载力远低于受拉斜撑。这充分说明延性剪切薄板在受剪屈曲后，其主拉方向提供较大水平承载力；其主压方向由于屈曲导致水平承载力贡献程度有限。两个截面水平内力之和与试件SN1所施加的总水平承载力518 kN误差不超过3%。此外，从试件SN1的Mises应力云图可知，该支撑的主应力方向与斜撑对角方向重合，剪切薄板并非全部屈服，剪切钢板角部区域应力水平较低，仍处于弹性阶段。这说明剪切薄板并未完全得到充分利用，其原因是剪切薄板的边缘钢板约束不足。为便于简化模型的推导，现引入有效宽度“S”的概念，用于反映仅在有效宽度范围内的剪切薄板为整个结构提供水平承载力、刚度和耗能等。

图8 SN1试件的滞回曲线

图9 SN1试件显著屈服时的Mises应力分布

3 DTSP钢支撑简化模型的理论推导

3.1 DTSP钢支撑的简化几何模型

在进行多层结构的滞回性能分析时，精细化有限元模型不易实现。因此，提出了一种合理的简化滞回模型来分析DTSP钢支撑的滞回性能。DTSP钢支撑主要由钢梁、钢柱、斜撑、边缘约束钢板及剪切薄板等部分组成。简化后，钢梁、钢柱采用相同截面的杆系单元模拟。斜撑、边缘约束钢板和剪切薄板则需综合考虑三者的承载力、刚度等性能，采用两根拉压不同性的交叉杆模拟，见图10。其中，钢梁、钢柱、交叉杆与地面间均采用铰接。

3.2 DTSP钢支撑的简化物理模型

图10 DTSP钢支撑的CBSM模型

3.2.1 DTSP等效交叉杆σ＇t、σ＇c应力的确定 由DTSP钢支撑滞回性能可知，两根交叉斜撑一根受拉、一根受压，并且受拉斜撑的水平承载力远高于受压斜撑的水平承载力。因此，简化模型的交叉等效杆应采用拉压不同性杆，且钢板等效杆的受拉水平承载力Ft＇应等于精细化模型中受拉斜撑的水平承载力Ft，钢板等效杆的受压水平承载力Fc＇应等于精细化模型中受压斜撑的水平承载力Fc。通过在延性剪切钢板中引入有效宽度概念，用于计算精细化有限元模型剪切薄板的受拉水平承载力Ft按公式（1）计算

式中，tw为延性剪切钢板的厚度；θ为支撑与水平方向的夹角；fy为延性剪切钢板的钢材屈服强度；S为延性剪切钢板的有效宽度。

精细化有限元模型中剪切薄板的受压水平承载力Fc可按公式（2）计算

式中，fc为延性剪切钢板屈曲时的受压应力；其他参数同前。

交叉杆简化模型中钢板等效杆的拉、压水平承载力可按公式（3）、（4）计算

式中，Ft＇为CBSM模型中斜撑的受拉水平力；Fc＇为CBSM模型中斜撑的受压水平力；σt'为CBSM模型中斜撑受拉应力；σc'为CBSP模型中斜撑受压应力；Ap为钢板等效杆的截面积。

因为 Ft=Ft＇、Fc=Fc＇，由此可得

因此，可根据水平承载力相等原则，建立CBSM模型中拉压异性杆的恢复力模型。

3.2.2 DTSP等效交叉杆E'的确定 在保证精细化模型与交叉杆简化模型水平承载力相等的情况下，还需

确保两者刚度相等。DTSP钢支撑的精细化模型中斜撑的轴向刚度（K）为

DTSP钢支撑的交叉杆简化模型中钢板等效杆的轴向刚度为

式中，K'为CBSM模型中斜撑的等效轴向刚度；E'为CBSM模型中斜撑的等效弹性模量；其他参数同前。

当两者刚度相等时，则

3.2.3 DTSP等效交叉杆模型参数η、β的确定 为确保所提出来的等效交叉杆简化模型更具普适性，现基于精细化有限元模型对12个DTSP算例进行了分析，主要用于合理确定延性剪切钢板的等效宽度及等效交叉杆受压屈曲力。表2给出了层间位移角为0.5%时，精细化模型受拉斜撑和受压斜撑的水平轴力Ft、Fc。

表2 DTSP算例的斜撑轴力

为更合理地描述延性剪切钢板的参与贡献，使所提公式更为简便，对等效宽度S进行了无量纲化，引入有效宽度系数η，定义为有效宽度与总宽度的比值，按公式（10）计算

根据12个DTSP试件的数据分析结果，有效宽度系数η可按拟合公式（11）计算

此外，还需合理确定钢板等效拉压异性杆的受压屈曲应力。同样，为使公式简便，引入受压屈服应力系数β：定义为受压屈曲应力与受拉屈服应力的比值，按公式（12）计算

根据12个DTSP试件的数据分析结果，受压屈服应力系数β可按拟合公式（13）计算

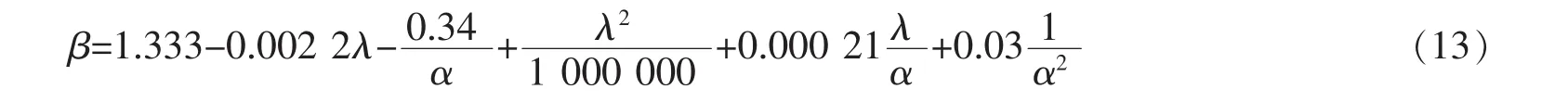
将公式（11）～（13）代入至公式（5）、（6）即可获得 CBSM 模型中拉压异性杆的循环应力-应变关系，见图11；通过上述公式再确定CBSM模型中等效拉压异性杆的滞回应力-应变关系曲线，见图11。

图11 等效拉压杆的滞回本构关系

4 DTSP钢支撑简化模型验证

4.1 DTSP钢支撑的宏观有限元模型

基于OpenSEES程序建立了SN1-SB4共计12个DTSP试件的交叉杆简化模型。其中，交叉杆简化模型的高跨比与精细化模型保持一致，钢板等效杆呈对角布置。钢梁、钢柱、等效交叉杆均为铰接，钢梁底端施加铰接约束。钢梁、钢柱截面与精细化模型保持一致，钢板等效杆截面积Ap按S·tw计算。

钢梁与钢柱采用Force Beam Column单元模拟，材料选择Steel01，采用Mises屈服准则考虑材料的包辛格效应。钢材初始弹性模量E取为2.06×105MPa，切线模量取0.02E倍，钢材屈服强度（fy）取为235 MPa。因周边钢梁与钢柱截面较大，故视为刚性杆。钢板等效杆采用Force Beam Column单元模拟，选择Hysteristic材料，该材料能模拟交叉杆的拉压异性特征。加载制度与微观有限元模型一致。

4.2 DTSP钢支撑的滞回曲线对比

图12所示为SN1-SB4共12个DTSP试件分别采用精细化模型和交叉杆简化模型分析得出的水平荷载-层间侧移角（P-δ）滞回曲线。

图12 滞回曲线对比

由图12可知，随着剪切薄板高厚比λ的增大及剪切薄板尺寸系数α的减小，DTSP钢支撑的水平承载力逐渐下降。随着荷载的增加，精细化模型的水平承载力略微增加，交叉杆简化模型的水平承载力略有下降，两者之间略有差异。此外，交叉杆简化模型分析的滞回曲线在二、四象限与精细化模型结果略有差异，在一定程度上交叉杆模型计算的二、四象限对应的残余承载力略低，但总体上能模拟DTSP支撑捏缩的滞回特性。虽然交叉杆简化模型获得的水平承载力比精细化模型分析结果略低，但出于偏安全考虑，该误差仍处于可接受范围内。在初始刚度方面，交叉杆简化模型分析的结果比精细化模型结果略低。对于卸载刚度交叉杆简化模型分析结果与精细化模型的吻合良好。综上所述，本文所提出的交叉杆简化模型可较好地模拟DTSP钢支撑的滞回性能。

4.3 DTSP钢支撑的累积滞回耗能对比

图13给出了试件SN1至SB4分别采用交叉杆简化模型和精细化模型分析所得的累积滞回耗能对比。其中，Etotal为试件的累积滞回耗能。

图13 累积滞回耗能对比

由图13可知，随着剪切薄板高厚比λ的增加和尺寸α的减小，DTSP钢支撑的累积滞回耗能逐渐减小。各试件的第一级荷载的耗能，简化模型小于精细化模型，这是因为交叉杆简化模型的初始刚度小于精细化模型，导致包络面积过小，耗能过小。在加载后期，尺寸系数为1/4和1/5的8个试件，交叉杆简化模型的累积滞回耗能略小于精细化模型，这说明当使用尺寸系数为1/4和1/5的DTSP钢支撑交叉杆简化模型设计时，设计结果偏保守；尺寸系数为1/3的4个试件，简化模型的累积滞回耗能比精细化模型的略高。总体上，DTSP钢支撑的交叉杆简化模型与精细化模型的累积滞回耗能拟合较好，说明交叉杆简化模型能较好地模拟DTSP钢支撑的累积滞回耗能。

5 结论

（1）基于DTSP钢支撑在循环荷载作用下的滞回特征，提出了此类结构可用于工程设计及工程分析的交叉杆简化模型。

（2）加载初期，交叉杆简化模型分析的DTSP钢支撑的水平承载力较精细化有限元模型分析结果略高；加载后期，交叉杆简化模型分析的DTSP钢支撑的水平承载力较精细化模型分析结果略低。

（3）交叉杆简化模型分析的DTSP钢支撑的初始刚度较精细化模型的分析结果略低；在卸载刚度方面，交叉杆简化模型分析结果与精细化模型的分析结果吻合较好。

（4）采用交叉杆简化模型分析的DTSP钢支撑的累积滞回耗能与精细化模型的分析结果相差较小，可较好地模拟DTSP钢支撑的滞回性能和耗能能力。