一种基于ILCD融合与多重分形去趋势波动分析的退化特征提取方法

王浩天， 段修生， 单甘霖， 孙 健， 王 兴

(1. 61716部队，福州 350000; 2. 陆军工程大学，石家庄 050003; 3. 石家庄铁道大学，石家庄 050003; 4.中国洛阳电子装备试验中心，河南 洛阳 471003)

液压泵在性能退化过程中，其振动信号呈现明显的非线性、非平稳性[1-2]。内部摩擦副间的相互作用，会以振动的形式沿多个方向传递到液压泵外表壳体[3]。为了提取完整的退化特征信息，需要采用合适的信息融合方法对多方向振动信号进行处理。

局部特征尺度分解法(Local Characteristic-scale Decomposition, LCD)能够将特征信息细化到不同的内禀尺度分量(Intrinsic Scale Component,ISCs)上，在迭代速度、分解能力和抑制模态混叠等方面较传统方法具有明显的优势[4-5]。郑近德等[6]提出了改良型局部特征尺度分解(Improved Local Characteristic-scale Decomposition,ILCD)方法，其采用分段多项式代替直线连接，有效减少了失真现象。但是，一些噪声及干扰分量仍然随机分布在部分ISC分量中，影响了特征信息的准确提取，且目前的ILCD方法只能处理单通道信号，无法实现多个信号的融合处理。为此，本文将高频谐波算法引入ILCD分解，并通过构建敏感因子和筛选准则，探索一种ILCD融合方法，改善重构信号中的特征信息。

此外，目前国内外对于性能退化特征提取的研究较少，导致现有特征无法有效反映退化过程，继而影响了故障预测的准确度[7]。多重分形去趋势波动分析[8-9](Multi-fractal Detrended Fluctuation Analysis,MF-DFA)是一种近年来提出的复杂度分析方法，相对其他复杂度分析方法，它更侧重于揭示隐藏在序列中内部的细节信息以及局部波动信息。采用MF-DFA可以获取液压泵振动信号序列的分形特征，从多重分形奇异谱角度对退化过程进行更佳的描述，且多重分形谱参数种类较多，有利于从不同层面不同角度描述液压泵退化过程。

为此，本文提出一种基于ILCD融合与MF-DFA的退化特征提取方法。首先，利用高频谐波与ILCD相结合，对多通道信号进行分解，并定义敏感因子，对ISC分量进行筛选并进行融合；在此基础上，利用MF-DFA方法对融合信号进行分析，提取多重分形谱敏感参数作为退化特征；最后，利用液压泵实测数据对本文所提方法进行验证。

1 基于ILCD的多通道信号融合方法

1.1 敏感分量的选取

考虑到ILCD对信号分解的特点，可以将高频谐波[10]算法与郑近德等的ILCD算法相结合，构造高频谐波信号

H(t)=Ucos(2πf)

(1)

x1(t)=x(t)+H(t)

(2)

式中：x(t)为原始信号;H(t)为高频谐波分量;U为幅值，通常取U=max(x(t));f为频率，通常取f=fs/2。

通过x1(t)的ILCD分解，获取ISC分量，这样可以将异常分量尽可能集中在第一个ISC分量中，便于敏感分量的选取。

一般来讲，互信息可以揭示变量间的非线性关系[11-12]。本文采用依据香农熵的公式

(3)

以互信息为基础，构建敏感因子λ作为筛选指标。设采样参数设置相同，所采集的正常信号为ynor，故障信号为yf，故障信号通过ILCD分解得到的第i个ISC分量为ISCi，则ISCi的敏感因子λi可定义为

λi=I1i-I2i

(4)

式中：I1i为ISCi与yf的互信息；I2i为ISCi与ynor的互信息。敏感因子λ最大值所对应的ISC分量，即为敏感分量。通过分析可知，通过对ICS分量的筛选，能够有效地减少噪声分量和干扰分量，更好地抓取敏感信息，提高特征的敏感度，从而改善对退化状态的表征能力。

在实际应用中，无法事先知晓被测信号是正常的还是故障的。但是，对于同一批次同样型号的样本，其在正常状态下的振动信号数据是可以测量和存储的，即式(4)中的ynor是可以得到的。因此，对于某样本当前状态下所测量到的信号，若其为正常信号，则经过ILCD分解后，根据式(4)可知，I1i与I2i是完全相同的，即所有ISC分量的敏感因子均为0，这也就表示不存在包含故障敏感信息的ISC分量；与之相对应的是，对于正常信号而言，其能量均匀分布在各个频带， ILCD分解所得的ISC分量中并不含有故障敏感特征信息的；对于故障信号而言，其能量集中在少数几个故障特征频带，在经过ILCD分解后，一些ISC分量中能够包含故障敏感信息，因此，通过分析可知，采用互信息的方法对ISC分量进行选取，能够有效地去除噪声分量和干扰分量，更好地抓取敏感信息，从而改善对退化状态的描述能力。

1.2 基于ILCD的信号融合

本文以三方向振动信号为例，对算法进行具体说明。根据上一节所定义的敏感因子λ，可以计算筛选出的ISC分量融合权值。设ISCi-j为第i个信号所选筛选出的敏感分量，λi为相应的敏感因子，i=1,2,3, 则可以得到其融合权值ki。加权融合重构的信号xFinal可描述为

(5)

因此，基于ILCD的多通道信号融合方法可描述为：①采集正常条件以及故障条件下液压泵三方向振动信号Xxnor,Xynor,Xznor和Xx,Xy,Xz，利用带有高频谐波的ILCD算法，分别对Xx,Xy,Xz进行分解，得到相应的ISC分量集；②利用式(4)计算Xx各ISC分量的敏感因子λ，选取出最大λ所对应的分量ISC，作为Xx信号的敏感分量，分别计算Xy和Xz各ISC分量的敏感因子λ，得到相应的敏感分量ISC以及相应的λ；③根据各敏感分量所对应的λ，利用ki进行加权融合，得到重构后的信号xFinal，即为液压泵振动信号的预处理结果。

通过分析可知，由于对信号的ILCD分解以及ISC分量的筛选，各方向原始信号中的噪声以及干扰分量得以有效减少，所选择的敏感分量中包含了非常重要的特征信息，继而通过后续的加权融合，对这些信息进行综合利用，得到重构信号，能够有效地提取隐藏在原始信号中的特征，改善信息的完整性。

2 基于MF-DFA的退化特征提取

MF-DFA方法的基本思想是通过对时间序列的去趋势处理，估计出描述时间序列分形特性的多重分形谱，揭示隐藏在序列内部的动力学行为信息[13]。文献[14]指出，原MF-DFA方法中对于数据分割的逆序处理，会一定程度地增加广义Hurst指数h(q)的误差。通过进一步分析可知，原MF-DFA方法存在多项式拟合过程的数据区间不连续问题，这也会产生一些新的伪波动误差。上述缺陷问题会导致最终的多重分形谱无法准确地刻画原始信号的多重分形特性信息。为此，可以采用加窗的方法来解决此问题，利用窗口相互重叠的连续区间，取代原方法中的不重叠区间。具体为：

步骤1设xi(i=1,2,…，N)为一非平稳时间序列，计算xi对其均值的累计离差，构建新序列X(k)；

步骤2设滑动窗口长度为u，每次步进为1，利用加窗法对新序列X(k)进行分割，可得到N-u+1段数据；

步骤3利用最小二乘法对每段数据进行多项式拟合，计算相应的方差均值

β=1,2,…,N-u+1

(6)

步骤4确定全序列的q阶波动函数

(7)

步骤5计算第q阶波动函数Fq(s)与时间尺度s间的幂律关系，得到广义Hurst指数h(q)

Fq(s)∝sh(q)

(8)

步骤6计算奇异指数α和多重分形谱f(α)

α=h(q)+qh′(q)

(9)

f(α)=q[α-h(q)]+1

(10)

根据上述计算过程可知，本文引入加窗方法，解决了数据区间分割的不连续性(步骤2～步骤4)，避免了为补足尾部数据所进行的反向分割操作所造成的数据混乱问题，提高了对信号多重分形特性的刻画效果，改善了对内部动力学行为特性的揭示能力。

多重分形奇异谱f(α)能够精细刻画时间序列的内部动力学特性，其主要特征参数[15]有f(α)的左右端点和极值点的横坐标α+∞，α-∞和α0，谱宽Δα以及端点差值Δf。α+∞和α-∞表示最大波动和最小波动所对应的奇异指数，能够从一定程度反映信号的波动性，但是对能量变化的敏感性较差；Δf刻画了振动信号大小峰值所占比例，能够从一定程度描述信号的多重分形特性，但是其稳定性较差，对退化过程的区分度较低；α0描述了振动信号不规则性和波动程度，具有良好的稳定性；Δα表征了信号多重分形特性的强弱，对退化过程具有较高的敏感性[16-17]。因此，本文选取α0和Δα为敏感参数，构成退化特征向量。

3 实验数据验证

为进一步验证本文所提方法的有效性与实用性，将其应用于液压泵的实测信号中。以松靴故障为例，随着退化程度的加剧，柱塞球头与滑靴的间隙不断增加，因此，可以利用间隙距离来描述退化程度。分别选用正常、松靴间隙0.15 mm，0.24 mm，0.38 mm和0.57 mm五种柱塞分别进行实验，描述松靴退化的不同阶段(正常以及F1～F4松靴故障状态)，如图1所示。

图1 实验柱塞Fig.1 Experimental pistons

实验用液压泵型号为SY-10MCY14-1EL，共有7个柱塞(每次选用实验柱塞更换其中1个柱塞)，额定转速为1 480 r/min，周期为0.041 s。将加速度传感器S1,S2和S3分别安装在泵端盖正面和侧面，采集双通道振动信号，如图2所示。采样频率为12 kHz，采样时间为1 s，将采集到的振动信号存入电脑。

图2 振动传感器的安装Fig.2 Installation of vibration sensors on hydraulic pump

以松靴0.24 mm为例(F2状态)，设传感器S1，S2，S3所采集的信号分别为X1，X2，X3。利用带有高频谐波的ILCD对X1进行处理，得到8个ISC分量以及1个趋势项u(t)。利用S1按相同参数采集正常条件下振动信号X1nor，分别计算每个ISC分量的敏感因子λ，结果分别为-51.26，0.315，0.963，2.621，4.836，2.881，2.138，0.792。因此，将ISC1-5作为X1的敏感分量，其对应的最大敏感因子为λ1=4.836。ISC1-1，ISC1-4和ISC1-53个分量的频域情况，如图3所示。

图3 ISC分量频域图Fig.3 Frequency domain graph of ISC

通过分析可知，泵实际转速为1 480 r/min，转轴频率为1 480/60=24.6 Hz，共有7个柱塞，因此，液压泵振动信号固有冲击频率为24.6×7=172.2 Hz；而对于单松靴故障，其特征频率理论上应该等于或接近转轴频率24.6 Hz。图3中的主要峰值为转轴固有频率(24.6 Hz)和固有振动冲击频率(172.2 Hz)及其倍频。从图3(a)可以发现，通过高频谐波以及ILCD相结合，原始信号X1中的噪声以及干扰分量大多集中在了第一个分量ISC1-1中，该分量几乎不包含任何故障相关信息，因此，其敏感因子远远小于其它分量；从图3(b)可以看出，ISC1-4中已经能体现一部分特征信息，即固有频率信息172.2 Hz及其倍频，但松靴故障信息仍相对微弱；从图3(c)可以很清楚的看到，无论是松靴信息24.6 Hz，还是固有频率信息172.2 Hz都得到一定程度的体现，因此ISC1-5的敏感因子最高，表明其对特征信息的贡献值相对其它分量而言也是最大的，这与前面的分析是一致的。

采用相同的方法分别对信号X2和X3进行处理，筛选出的敏感因子分别为ISC2-4和ISC3-5，如图4所示，对应的敏感因子分别为λ2=3.021和λ3=2.892。

图4 敏感分量频域图Fig.4 Frequency domain graph of sensitive components

从图4可以看出，X2和X3信号筛选出的敏感分量ISC2-4和ISC3-5也均包含了相对清晰的松靴信息以及固有信息，与X1信号筛选出的ISC1-5相比，其特征信息比重相对较低，因此λ2和λ3的值均小于λ1。根据式(5)得到3个敏感分量融合权值为：k1=0.450，k2=0.281，k3=0.269，进行加权融合，重构信号为

xFinal=0.450ISC1-5+0.281ISC2-4+0.269ISC3-5

其频域情况如图5所示。为了对比ILCD融合方法较LCD融合方法的优势，以传统LCD方法为基础，与本文第一部分的敏感因子以及筛选重构准则结合，构建基于传统LCD的融合方法，对原始信号进行处理，最终结果如图6所示。

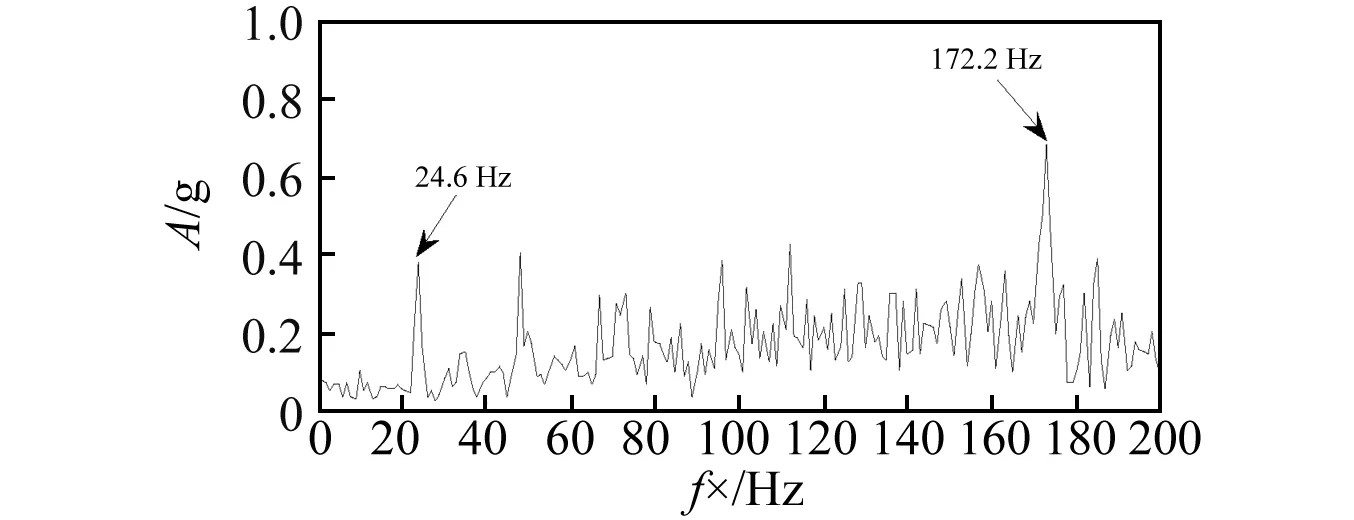
图5 基于ILCD的信号融合方法效果Fig.5 The processing effect by the ILCD signals fusion algorithm

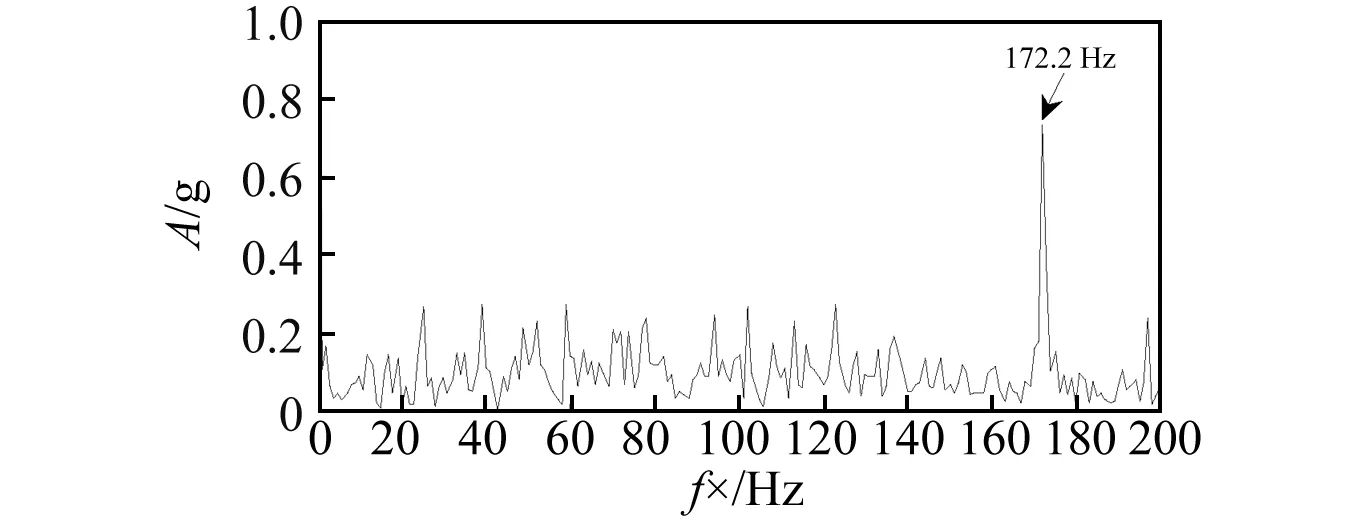
图6 基于传统LCD的信号融合融合方法效果Fig.6 The processing effect by the traditional LCD signals fusion algorithm

从图5可知，采用基于ILCD的多通道信号融合方法进行预处理，初步提取了所需的故障特征信息，可以清晰地看到松靴故障特征频率24.6 Hz以及固有振动频率172.2 Hz。通过图6与图5的对比分析可知，采用传统的LCD作为信号处理方法，由于直线连接模式存在与数据点交汇情况，造成部分分量的失真，影响了对关键故障特征频率信息24.6 Hz的获取，仅仅能够获得172.2 Hz的固有频率信息，这会一定程度地影响后续所提取退化特征的表征能力。

在此基础上，为了进一步对比ILCD融合方法较ILCD单通道处理效果的优势，利用ILCD方法对X1信号进行处理，结果如图7所示。

图7 基于ILCD的单通道信号处理效果Fig.7 The processing effect of single signal by the ILCD

通过分析图7可知，由于液压泵自身特点，其特征信息比较微弱，单通道包含的特征信息有限，因此，利用ILCD方法仅对单通道信号进行处理效果不佳，干扰成分较多，无论是特征频率信息24.6 Hz还是固有频率172.2 Hz，均不显著。通过对比图5与图7可以很清楚地看到，采用ILCD融合方法能够充分利用各个通道所包含的关键信息，剔除无用的干扰分量和噪声分量，有效地获取所需的频率分量，满足后续退化提取需求。

采用同样的参数设置，分别对F1～F4每个阶段各采集10组数据，共50组。通过ILCD融合处理后，分别利用第2部分的MF-DFA方法计算α0和Δα，如图8和图9所示。

图8 F1～F4阶段的α0Fig.8 α0 of F1—F4

图9 F1～F4阶段的ΔαFig.9 Δα of F1—F4

图8描述了F1～F4阶段α0的取值情况，随着退化程度的加深，α0的取值呈现下降趋势，而对于每一条曲线而言，高组别的α0值也基本小于低组别的α0值，这符合性能退化的变化规律；各条曲线虽然存在一定的波动，但是幅度比较小，表明α0具有较好的稳定性；曲线间的交叉比较少，主要存在于F1和F2两条曲线间，而F1和F2为松靴故障退化的初始阶段，振动信号不规则程度较高，且故障信息比较微弱，影响了α0的敏感度；对于F3和F4阶段，可以发现各条曲线间不存在交叉，且间距较大，表明α0对松靴故障退化的中后期具有较高的敏感性和识别能力。

图9为F1～F4阶段Δα的变化情况，由于振动信号的多重分形特性随着退化程度的加剧而不断增强，因此，Δα的整体取值呈现上升趋势；F1～F3状态所对应的曲线波动并不是很明显，而F4所对应的曲线出现了比较明显的波动振荡现象，这是因为在松靴退化后期，振动信号随机性与复杂性发生了很大改变，导致Δα无法准确地提取局部波动信息，影响了其稳定性，这与图6所反映的情况是一致的；各条曲线间的交叉比较少，相互存在比较明显的间距，表明Δα对性能退化前期和中期具有较好地表征能力。

为了验证本文所提方法的优势，仍采用前面所提的基于传统LCD的融合方法对同样的50组数据分别进行处理，经MF-DFA方法分别计算α0和Δα，结果如图10和图11所示。

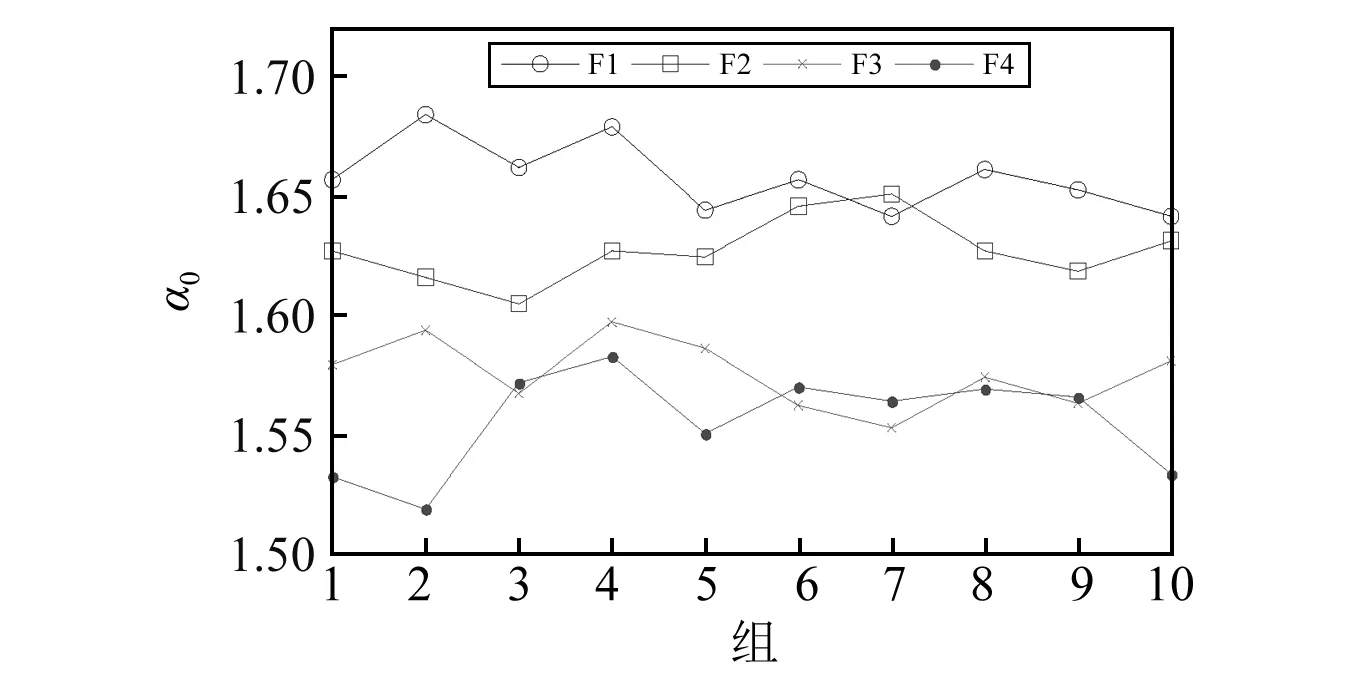
图10 基于传统LCD融合处理得到的F1～F4阶段的α0Fig.10 α0 of F1—F4 by traditional LCD fusion

图11 基于传统LCD融合处理得到的F1～F4阶段的ΔαFig.11 Δα of F1—F4 by traditional LCD fusion

图10和图11分别描述了采用基于传统LCD融合方法所得到的F1～F5阶段α0和Δα的变化情况，与图8和图9相比，图10中F1～F4对应的α0曲线波动有一定程度地增加，且存在较明显的交叉现象，对局部退化过程的表征能力有所下降；图11中F1,F2,F3和F4对应的Δα曲线间距较近，且部分曲线变化呈现带有明显波动的无规律趋势。造成上述现象的原因在于LCD算法的固有缺陷，使得信号分解所得的部分内禀尺度分量失真，造成部分关键信息的遗失，影响了多重分形谱特征性能。

在上述定性分析的基础上，接下来采用双样本Z值检验法，进行定量评价。Z值越大，该特征对不同故障程度的区分能力越强，敏感度越高，计算公式为[18]

(11)

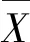
表1 各特征量对松靴退化过程的敏感度Tab.1 Sensitivity of features to degradation of loose slipper

由表1可知，小波融合-MFDFA方法所提取的多重分形特征参数的敏感度均值最低，对各个状态的区分能力也非常有限；LCD融合-MFDFA方法提高了对故障信息的挖掘能力，敏感度得到了一定提升，但由于受到LCD分解失真问题，影响了其对退化状态的敏感度；本文所提方法采用ILCD解决了分量失真问题，且对敏感信息进行了深入、准确地挖掘，因此所提取的多重分形谱参数特征，无论是对单个双样本的区分能力，还是整体平均敏感度，都具有比较明显的优势，这与前面定性分析的结论是一致。

4 结 论

本文提出了一种基于ILCD融合与MF-DFA的退化特征提取方法，并利用实测信号进行了验证，主要结论如下：

(1)提出一种基于ILCD的多通道信号融合方法，将高频谐波与ILCD结合，通过定义敏感因子对ISC分量进行筛选，实现多通道信号的融合重构，有效减少了干扰成分的影响。

(2)采用加窗区间分割改进MF-DFA方法，解决数据分割不连续所产生的伪波动误差，避免了关键特征信息遗漏，改善了特征对性能退化过程的表征能力。

(3)实验结果表明，本文方法所提取的退化特征，能够较好地反映液压泵性能退化过程，对于视情维修的开展具有重要意义。