弹性支座对简支箱梁桥振动特性的影响及隔振效果研究

罗 锟, 汪振国, 雷晓燕, 欧开宽, 张新亚

(华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌 330013)

高架桥梁结构的振动与噪声问题一直都是丞待解决的重要课题。混凝土桥梁结构振动会向四周辐射低频噪声(20～200 Hz)，该频段噪声对人的注意力、反应时间及语言辨识能力等有诸多负面影响[1-2]。振动为噪声之源，因此，对桥梁结构的振动特性开展研究，寻求减少桥梁结构振动的合理措施，对降低桥梁结构低频噪声、保障人体身心健康和促进桥梁行业的发展都具有重要意义。

桥梁支座是连接桥梁上部结构与桥墩的重要结构部件，也是桥梁结构振动传递的必经途径，目前，国内外针对减(隔)振支座的研究相对成熟，其在混凝土结构的振动控制中已得到初步应用。文献[3]实测了某公路桥梁支座上下部节点的加速度响应，发现支座下部节点的加速度响应小于上部节点的加速度响应；文献[4-5]利用实时混合模拟方法，对设有隔震支座的土工结构开展研究，探讨了土工系统整体抗震性能；文献[6-7]建立了车桥耦合模型，通过仿真分析了支座刚度变化对耦合系统振动的影响，并定量研究了弹性支座的隔振效果；文献[8]以三跨混凝土连续梁桥为对象，对摩擦摆支座应用后的隔振效果进行了研究；文献[9]介绍了一种新型滑移支座，并研究了该种支座的摩擦性能与隔振效果；文献[10]介绍了减振支座在实际桥梁中的隔振应用；文献[11]设计了一种三维隔振支座，并介绍了其在房屋结构上的减振应用。

可以发现，以往研究多关注减(隔)振支座的设计、应用以及对车桥耦合系统整体动力响应的影响，然而，桥梁结构噪声辐射与桥梁中高频(20～200 Hz)局部振动特性相关，且桥梁各板件的振动是结构噪声产生的根源[12]，弹性支座在中高频段(20～200 Hz)内对桥梁各板件振动特性的影响却鲜有文献报道。

本文便以32 m简支箱梁桥为原型，以10∶1为几何缩尺比，设计制作了研究桥梁结构振动特性的简支箱梁相似模型，并推导了原型桥与模型桥间的相似关系，进而对原型桥与模型桥有限元模型进行模态分析，以及开展相似模型的模态试验，通过模态数据对比来验证相似模型的可靠性。在此基础上，通过锤击试验，研究不同竖向刚度的弹性支座在20～200 Hz频带内对桥梁各板件振动特性的影响，并探讨了弹性支座在箱梁桥上部结构与桥墩间的隔振效果。

1 模型试验相似理论

1.1 相似条件

模型与原型之间保持严格的动力、静力相似，有四个必要和充分的相似条件：

(1)几何相似。模型和原型的几何尺寸需保持一定的比例，即

L/Lm=λ

(1)

式中：L为原型的几何尺寸；Lm为模型的几何尺寸(下标“m”代表模型中的物理量，下同)；λ为几何比尺。

(2)物理性能相似。两者的质量与材料密度需保持一定的比例，即

(2)

式中：M为质量；ρ为材料密度；λρ为密度比尺。

(3)运动相似。模型与原型相应质点的速度和加速度应保持一定比例，这就相当于两者在动力过程中所经历的相应时段保持一定的比例，即

(3)

f/fm=tm/t=1/λt=λf

(4)

式中：v为速度；a为加速度；t为时间；f为频率；λv,λa,λt,λf分别为速度比尺、加速度比尺、时间比尺和频率比尺。

(4)动力相似。在动力过程中，无论由什么原因所产生的作用力，其比尺应保持一致，即

F/Fm=λF

(5)

式中：F为作用力；λF为作用力比尺。

在动力作用过程中，对结构的动力性质产生影响的有重力、惯性力、弹性恢复力及其他外作用力，它们相应的作用力比尺为

重力：F/Fm=(ρ/ρm)·λ3

(6)

(7)

弹性恢复力：F/Fm=(E/Em)·λ2

(8)

式中：E为材料弹性模量。

其他作用力，令其比尺为P/Pm，则

F/Fm=P/Pm

(9)

由式(5)～式(9)得

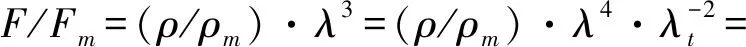
(10)

可以发现：相似条件(1)、条件(2)、条件(3)分别为我们提供了三个相互独立的比尺λ,λρ,及λt，而相似条件(4)则限制了这三个比尺的关系。在相似模型设计时，要使原型与模型间各比尺满足式(10)几乎是不可能的，我们只能根据试验目的及要求，近似或部分地满足式(10)的要求。林皋等[13-14]曾根据不同的试验目的及要求，指出结构动力模型试验有3种基本换算关系：弹性力相似律、重力相似律及弹性力-重力相似律。其中，以研究结构振动特性以及弹性阶段结构动力响应为试验目的时适用弹性力相似律。

1.2 弹性力相似律

弹性结构振动方程如下

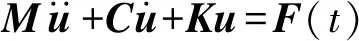
(11)

式(11)表明，影响结构振动的主要作用力为惯性力、阻尼力与弹性恢复力。在研究结构振动特性时，可主要保持惯性力与弹性恢复力相似，据式(7)、式(8)、式(10)可推出

(12)

整理得

糖尿病是一种慢性代谢疾病，患者体内的胰岛素分泌不足，导致血糖异常升高。糖尿病患者通常会合并其他的疾病（肝胆结石或是胰腺肿瘤等）。在肝胆胰疾病患者合并糖尿病之后，会增加手术的难度，在手术中容易出现异常情况，引发各种并发症，手术效果旺旺达不到预期值，或是更差[5-7]。而对患者进行围手术期护理，不仅能够降低手术风险，还能够改善患者预后。

(13)

当研究结构在弹性阶段的动力响应时，还应保持作用力F的相似，由式(10)得

λF=F/Fm=(E/Em)·λ2

(14)

此外，支座刚度比尺λK可由作用力比尺λF与位移比尺λu表示，即

λK=(F/u)/(Fm/um)=λF/λu

(15)

式中：u为位移，其量纲与几何尺寸量纲相同，故其比尺λu与几何比尺λ相同。

由此可见，当以弹性力相似律指导相似模型设计时，材料的弹模比尺λE、密度比尺λρ和几何比尺λ是相互独立的，可供我们选择，在此基础上可导出其他各相关物理量的比尺。由于不用考虑模型的材料问题，这将使得相似模型的制作更加便携，并降低试验成本。

2 箱梁相似模型设计与制作

2.1 简支箱梁原型桥参数

简支箱梁原型桥长32 m，采用C50混凝土材料浇筑，其计算跨径31.40 m，桥面宽12.00 m，梁高3.05 m，箱梁横截面尺寸如图1所示。C50混凝土材料弹性模量E=34.5 GPa，密度ρ=2 500 kg/m3。

2.2 简支箱梁相似模型桥参数

模型桥梁各几何尺寸均为原型桥梁的1/10，浇筑材料采用H60-Ⅲ型灌浆料，采用应变片法测灌浆料的弹性模量，万能压力机对3组灌浆料试块施加压力，

应变信号采集仪采集应变值，依据胡克定律得到比例极限内应力应变关系，材料的弹性模量即可依据此关系得出。试验得到该灌浆料平均弹性模量Em=30 GPa。对12组灌浆料试块进行称重，并测量试块体积，再确定各试块的密度值，最终得到该灌浆料平均密度ρm=2 203 kg/m3。制作的箱梁相似模型桥如图2所示。

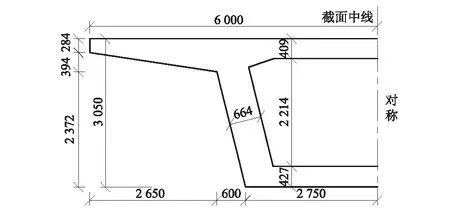
图1 箱梁横截面几何尺寸(mm)Fig.1 The geometry dimension of box girder cross section

图2 简支箱梁桥相似模型Fig.2 The similarity model of box girder bridge

依据弹性力相似律，在已知原型与模型材料的弹模比尺λE、密度比尺λρ和几何比尺λ后，可导出其他各相关物理量的相似比尺，模型试验各比尺如表1所示。

表1 模型试验相似比尺

2.3 弹性支座的制作及刚度测定

为得到不同刚度的模型支座，针对同种橡胶材料，设计了3种不同几何尺寸的弹性支座，如图3所示。利用刚度测定装置分别测量3类支座的压缩刚度，如图4所示。

图3 弹性支座Fig.3 Elastic supports

1-千斤顶; 2-位移传感器; 3-夹板1;4-压力传感器; 5-橡胶支座; 6-夹板2图4 弹性支座刚度测定装置Fig.4 The stiffness measuring device of elastic support

表2 支座刚度测定结果

3 箱梁相似模型校验

3.1 相似比尺校验

利用ANSYS软件分别建立箱梁相似模型桥与原型桥的有限元模型，两者梁体均采用solid45单元模拟，材料参数于上文给出，并在有限元模型支座处施加固定约束，模拟支座刚度为刚性时的约束状态。之后对两者进行模态分析，通过对比两者的模态频率是否满足上文推导的频率比尺来初步校验相似比尺推导的正确性。表3给出两箱梁有限元模型前5阶模态频率比尺的对比结果。

表3 原型梁与模型梁各阶频率比尺校验

从表3可以看出，模态分析得到的模态频率比尺和推导得到的频率比尺相差极为微小，表明频率比尺计算结果正确，初步校验了相似比尺的正确性。

3.2 相似模型模态测试

对浇筑的箱梁相似模型进行模态测试，将测试结果与有限元模态分析结果进行对比，以此校验相似模型的正确性。为保证制作的相似模型与有限元相似模型具有相同的约束方式，在支座处将分别固定在箱梁体及桥墩上的钢板焊接在一起，如图5所示。

采用LMS Test. Lab软件的MIMO FRF Testing模块测定相似模型的模态，该模块内置多种信号源，测试

图5 支座处的约束方式Fig.5 The restraint mode at the support

时输出猝发随机信号，信号经功率放大器放大，再输出至激振器，激振器将信号以力的形式作用在结构上形成激励，信号采集仪通过传感器采集结构的振动信号与力信号，再经软件实时处理形成频响函数，借助软件内置的PolyMAX模态参数估计算法，对频响函数进行分析处理即可确定结构的模态，模态测试流程如图6所示。信号采集仪使用比利时LMS公司310数据采集系统(24通道数据采集系统，A/D 24位)；振动传感器采用PCB356A16型三向加速度传感器(灵敏度：100 mv/g；量程±50g；频响范围：0.3～6 kHz)；力传感器型号为PCB208C02，灵敏度10.91 mv/N，动态范围为±450 N。

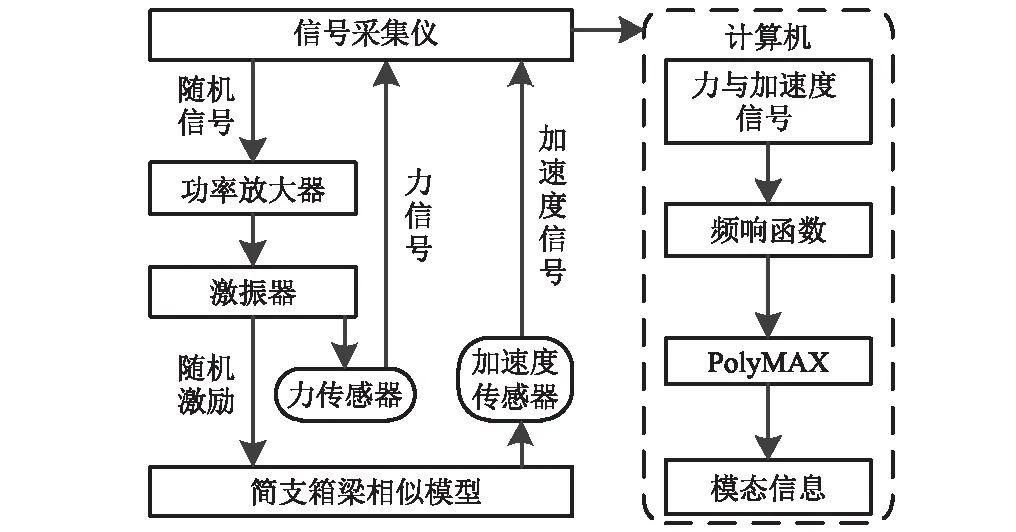
图6 模态测试流程Fig.6 The flow chart of modal testing

沿箱梁长度方向每隔0.4 m选取一个断面，每个断面布置8个拾振点，全梁共计72个拾振点；激振点布置在第一个断面翼板处，以箱梁第一个断面为例，其拾振点与激振点布置如图7所示。

图7 拾振点与激振点布置Fig.7 The layout of receiver points and exciting point

所有测点采集的加速度信号经过处理形成频响函数，模态参数估计算法对这些频响函数进行处理与模态识别，在0～150 Hz的频率范围内共识别5阶模态，其模态置信度矩阵如图8所示。

图8 模态置信度矩阵柱状图Fig.8 The histogram of modal assurance criterion

由图8可知：模态置信度矩阵非对角元最大值为9.184%，其余均小于7%；矩阵对角元值均为100%。这表明所识别的各阶模态具有较好的独立性。选取前5阶实测模态频率与有限元模态分析频率进行对比，列于表4，图9给出前5阶振型对比，其中左侧为实测模态振型，右侧为有限元模态分析振型。

表4 模态频率对比

图9 模态振型对比Fig.9 The comparison of modal shapes

由表4及图9可知：前5阶模态频率与振型的对比结果吻合较好；第2阶实测模态频率与有限元模态频率的误差相对较大，为5.44%，但两者在该阶次的振型相近，误差相对较大的原因可能是激振点或拾振点的设置不足导致的；可从整体来看，箱梁桥实际相似模型与有限元模型还是具有较好的一致性，表明箱梁桥相似模型制作正确。

4 箱梁导纳特性试验

4.1 试验原理

导纳是傅里叶变换后的输出响应和输入激励信号的比值，其反映的是结构自身的固有振动特性，和输入的激励无关。锤击试验，即给结构施加一个脉冲激励，同时采集输入激励信号和输出响应信号。锤击激励一次相当于在所要研究的频率范围内都进行了一次试验，这一过程又称扫频[15]。锤击激励作用下，结构振动方程为式(11)，其中外作用力F(t)在此处为锤击力。将加速度和锤击力的时域信号进行傅里叶变换，则加速度导纳HAF(ω)可表示为

(16)

本文采用锤击试验获取模型桥上关注测点的加速度导纳，再将其按需要分析的频率范围反演到箱梁原型桥上，以此分析箱梁桥的振动特性。锤击试验所用加速度传感器和信号采集仪与上文模态测试所用设备相同，力锤采用PCB086D05型力锤(灵敏度为0.23 mv/N；量程为22 kN；谐振频率≥22 kHz)。

原型箱梁桥需分析20～200 Hz内的频率，由频率比尺λf可知，相似模型就需分析198～1 987 Hz内的频率，图10为锤击力的时程与功率谱密度(Power Spectral Density, PSD)曲线，可以看出锤击力在0～2 000 Hz频段内均具有较大的锤击能量，可激起较大的振动，表明锤击试验是可行的。

(a)时程曲线

(b)功率谱密度曲线图10 锤击力时程和功率谱密度曲线Fig.10 The hammer force time historyand power spectral density curve

4.2 支座刚度对箱梁振动特性的影响

选择跨中截面作为分析截面，在该截面的顶板、翼板、腹板与底板处设置观测点，锤击点与顶板观测点相同，如图11所示。

图11 跨中截面观测点布置Fig. 11 The arrangement of observation points at mid-span

考虑不同支座刚度(刚性、A号、B号及C号支座)对跨中截面各观测点振动的影响，分析各观测点的加速度导纳特性。图12为各观测点在不同类型下的加

速度导纳曲线。

从图12可以看出：在20～110 Hz的频率范围内，除极个别的频率外，各观测点在不同支座刚度下的加速度导纳曲线近乎重合，这表明在该频段内，支座刚度变化对箱梁跨中的振动影响很小；在110～200 Hz的频带内，各导纳曲线开始出现偏差，但偏差较小，这表明在20～200 Hz的中高频段范围内，支座刚度变化会对箱梁跨中的结构振动产生一定的影响，但影响很小。此外，通过对比图12中相同支座条件下跨中各测点的加速度导纳曲线可以发现：顶板加速度导纳最大，翼板次之，再者腹板，底板加速度导纳最小，这说明振动由顶板传递至翼板的过程中衰减慢，其次是腹板，振动由顶板传递至底板的过程中衰减最快。通过观测跨中腹板的加速度导纳曲线可以发现：其峰值频率主要集中在30～80 Hz的频段内，其它频率下的幅值相对较小，这表明箱梁腹板在该频段内会出现密集的局部振动模态。

图12 跨中截面各观测点加速度导纳曲线Fig.12 The acceleration admittance curves of observation points across mid-span

4.3 弹性支座隔振效果分析

为探讨不同支座的隔振效果，以墩顶的加速度导纳为研究对象，在跨中顶板处施加竖向锤击激励，跨中翼板处施加横向锤击激励，分析不同支座刚度下桥墩顶面中心点的振动响应。图13为锤击点与桥墩测点图示。图14为锤击荷载下各支座刚度下墩顶测点竖向加速度导纳的频谱与1/3倍频程频谱曲线，图15为墩顶测点横向加速度导纳的频谱曲线。

从图14(a)可以看出：墩顶的竖向振动在52 Hz时出现较大峰值，在97～114 Hz及171～200 Hz的频率范围内峰值较大，表明桥墩顶面在上述频率或频带内的竖向振动强烈，在桥梁结构减振设计时，应给予重点关注；在上述频率频率或频带内，刚性支座下的加速度导纳峰值均要大于其他支座类型，尤其是52 Hz处及180～200 Hz内的导纳幅值，这表明桥梁上部结构与桥墩间设置弹性支座可有效降低墩顶的竖向振动。

图13 跨中锤击点与墩顶观测点Fig.13 The hammering points in mid-span and pier top observation point

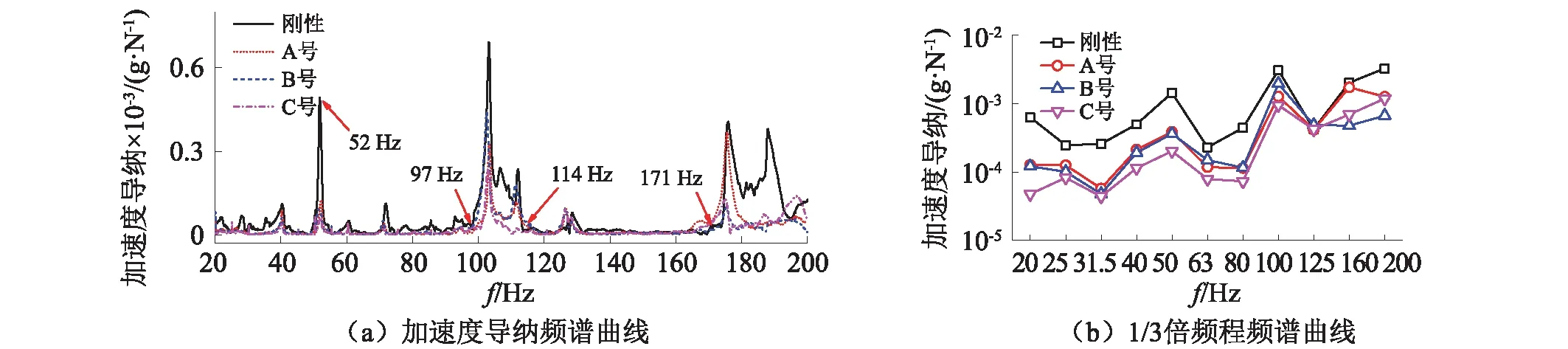
图14 墩顶测点竖向振动Fig.14 The vertical vibration of measuring points at pier top

图15 墩顶测点横向加速度导纳频谱曲线Fig.15 The transverse acceleration admittance spectrum curve of measuring point at pier top

由图14(b)可以发现：中心频率为50 Hz(频率范围45～56 Hz，包含52 Hz)时，A支座与B支座下的加速度导纳相差不大，但整体上呈现出支座刚度越小，隔振效果越好；中心频率为100 Hz(频率范围89～112 Hz，包含97～114 Hz范围内大部分频率)时，C支座隔振效果最好，其次为A支座，B支座隔振效果最差；中心频率为160 Hz与200 Hz(包含171～200 Hz)时，B支座隔振效果最好，其次为C支座，A支座隔振效果最差。

从图15可以看出：墩顶的横向振动主要集中在71 Hz和126 Hz处，表明桥墩顶面在上述频率处的横向振动强烈，在桥梁结构减振设计时，应给予重点关注；当频率为71 Hz时，刚性支座下墩顶横向加速度导纳最大，其次为B支座，再者A支座，C支座下的墩顶横向加速度导纳最小，表明该频率下C支座隔振效果最好，B支座的隔振效果最差；当频率为126Hz时，弹性支座的刚度越小，隔振效果越好。

由此可见，支座刚度的大小对弹性支座的隔振效果有很大影响，但两者并不呈现出单一的变化规律，而是与所分析的频率有关，故在实际选用桥梁弹性支座时，应综合考虑支座刚度与减振频段这两个因素。

5 结 论

本文依据弹性力相似律设计制作了简支箱梁桥的相似模型，并在模型中嵌入3种不同刚度的模型支座，通过开展锤击试验，研究了支座刚度变化对箱梁桥振动特性的影响，进一步地，分析了弹性支座在箱梁桥上部结构与桥墩间的隔振效果，得到如下结论：

(1)当以弹性力相似律指导相似模型设计时，由于不用考虑模型的材料问题，这将使相似模型的制作更加便携，并降低试验成本。

(2)在20～200 Hz的中高频段范围内，支座刚度变化会对箱梁跨中的结构振动产生一定的影响，但影响很小；振动由顶板传递至翼板的过程中衰减慢，其次是腹板，振动由顶板传递至底板的过程中衰减最快；箱梁腹板在30～80 Hz的频段内会出现密集的局部振动模态。

(3) 简支箱梁桥上部结构与桥墩间设置弹性支座可有效降低墩顶的振动，且支座刚度的大小对弹性支座的隔振效果影响很大，同时弹性支座在不同频率下的隔振效果差异较大，在实际选用桥梁弹性支座时，应综合考虑支座刚度与减振频段这两个因素。