基于次级通道在线辨识新算法交叉更新ANC 系统

袁 军，吕韦喜，刘东旭，张 涛

（重庆邮电大学 光电工程学院，重庆400065）

近年来，由于人均机动车保有量的增加，随之而来的交通噪声严重影响人们的身体健康。传统降噪方法采用被动噪声控制，即利用声学包装、安装消声器和设计隔声结构来降低噪声。这种方法因其在中高频率范围内的高衰减噪声而受到重视，但在较低的频率范围内所取得的降噪效果并不明显且体积大、成本高，应用场合受到限制。而主动噪声控制对低频噪声却有着很好的降噪效果[1]，因而受到很大的关注。

主动噪声控制作为噪声消除中的重要组成部分，在室内噪声消除中其设计所面临的主要挑战与有源噪声消除ANC（active noise cancellation）系统的收敛速度和降噪性能相关。由于自适应滤波器的权值更新采用最小均方LMS（least mean square）算法，该算法存在的主要问题是当潜在的输入过程在高度有色化时的慢收敛状态。由于真实的噪声环境中噪声信号的功率谱密度大都不是平坦的，甚至是高度有色化的，故在此采取修改的LMSN（LMS Newton） 算法来更新第3 个滤波器的权值。由于LMS 算法在对ANC 系统的次级通道收敛速度和建模精确度等方面较为不足，故在此采用变步长VSS（variable step size）LMS 算法来更新次级通道的建模滤波器的权值。

1 ANC 的基本原理和结构

1.1 ANC 的基本原理

有源噪声消除ANC 是根据声波的叠加原理，通过产生同等振幅并且相位相反的信号，进行消除主通道中噪声的方法。如图1 所示，使用滤波X 最小均方FxLMS（filtered X LMS）算法，P（z）是位于参考传声器和误差传声器之间的主路径，S（z）是跟随有源噪声消除自适应滤波器W（z）的次级路径，抗噪信号y′（n）由W（z）的输出y（n）而产生。y′（n）与主路径的噪声d（n）相结合以减少误差扬声器周围的声压。

图1 ANC 系统中FxLMS 算法框图Fig.1 Block diagram of FxLMS algorithm in ANC system

1.2 LMS 算法收敛分析

传统的ANC 系统采用LMS 算法更新权系数。LMS 算法是最陡下降算法的随机实现；简单地将瞬 时的粗略估计代替代价函数ξ（n）=E［e2（n）］。w（n）由以下方程式更新：

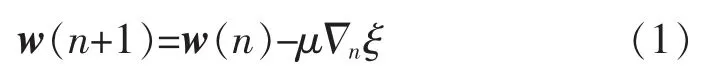
此外

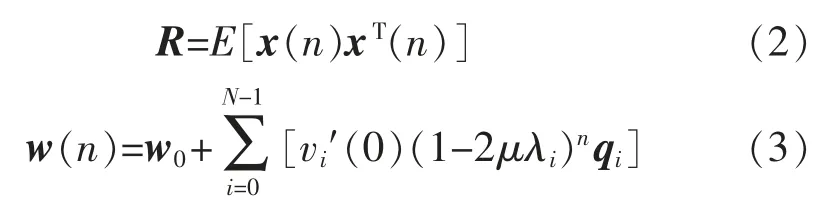
式中：q0，q1，…，qN-1为与λ0，λ1，…，λ（N-1）相对应的R 的特征向量。

其结果表明，对于N 抽头横向滤波器，最陡下降算法的暂态行为取决于N 个指数项之和，其中每个指数项由自相关矩阵R 的一个特征值所控制。每个特征值λi在对应的特征向量qi所定义的方向上确定了一个特定的收敛模式。不同的模式在相互独立地起作用。

离散时间平稳随机过程的｛x（n）｝的自相关矩阵R 的特征值介于该过程的功率谱密度Φxx（ejw）的最小值与最大值之间，即

为了保证最陡下降法的收敛性步长必须满足

为此可以看出，当噪声源产生的噪声信号功率谱密度不平坦的时候，在保证LMS 稳定性的前提下，必须使得步长μ 的取值很小，在这种情况下LMS 收敛速度会受到很大的影响。

2 次级通道在线建模的方法

2.1 现有结构

2.1.1 Eriksson 所提方法

在文献[2]中，Eriksson 所提出的次级路径在线建模系统如图2 所示。

图2 Eriksson 提出的次级路径在线建模系统Fig.2 Eriksson’s secondary path online modeling system

假设，控制滤波器W（z）是一个长度为L 的实权值FIR 滤波器，此时次级路径的信号y（n）为

其中

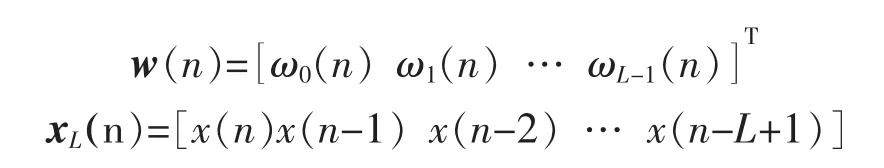
式中：w（n）为主控制滤波器的实权值向量；xL为参考信号选取L 个样本组成的向量；x（n）为通过参考麦克风而得到的参考信号。图中，v（n）为内部产生的零均值高斯白噪声，并与参考信号x（n）不相关，在输入中被注入控制滤波器中的y（n）。残余噪声信号e（n）被定义为

其中

式中：d（n）为在误差麦克风周围主要的干扰信号；y′（n）为次级消除信号；v′（n）为建模信号；p（n）和s（n）分别为主路径传递函数P（z）和次级路径传递函数S（z）的信道参数。残余误差信号e（n）是作为误差W（z）的误差信号，作为理想的响应，即g（n）=ds（n）=e（n）。因此W（z）和的误差信号分别为

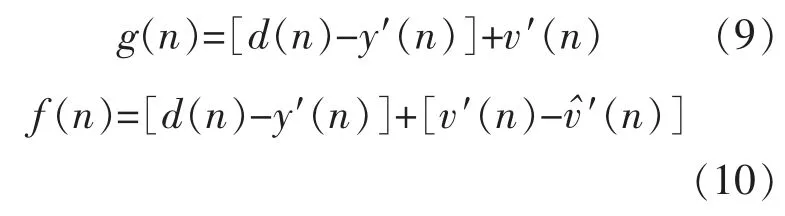
控制滤波器的系数由FxLMS 算法来更新，即

其中

式中：μw为控制过程的步长为参考信号x（n）通过建模滤波器卷积而来。显而易见，控制过程被不需要的干扰项所干扰。

其中

其中

式中：μs为建模滤波器的步长。由建模滤波器估计而来。由式（13）显示，建模过程的精度被误差μsv（n）［d（n）-y′（n）］所影响，在最坏的情况下建模的过程会产生发散的情况。

2.1.2 Zhang 所提方法

在文献[3]，Zhang 所提出的关于有源噪声消除系统的次级路径在线建模如图3 所示。

图3 Zhang 提出的次级路径在线建模系统Fig.3 Zhang’s secondary path online modeling system

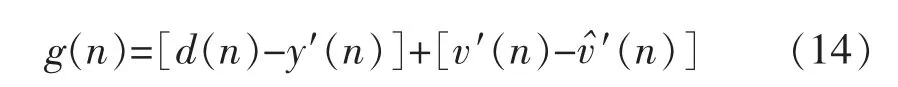
其中，误差信号g（n）被用作第3 个自适应滤波器的期望响应。因为H（z）由x（n）和g（n）所驱动，［d（n）-y′（n）］与x（n）相关，所以它的输出收敛于［d（n）-y′（n）］，输出信号u（n）=e（n）-H（z），从而为了得到理想的关于建模滤波器的响应，ds（n）=e（n）-u（n）。因此给出LMS 算法中的误差信号为

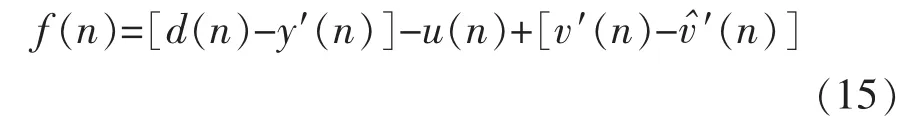
故

当H（z）收敛时，

因此，产生了适当的信号并希望提高性能，文献[8]所展现的交叉更新的有源噪声消除系统，在已有的方法中表现出了很好的性能。但是，该方法当参考信号的自相关矩阵的特征值极度分散的情况下，整个ANC 系统的收敛速度会受到很大的影响。

2.2 改进的结构

在此对Zhang 的方法所做的修改如图4 所示。使用VSS LMS[4-5]更新建模滤波器的权值，再用LMSN[6-7]更新第3 个自适应滤波器权值。

图4 提出次级通道在线建模算法Fig.4 Proposed algorithm for online secondary path modeling

为解决最陡下降法对于输入信号相关矩阵R=E［x（n）xT（n）］的特征值分散时，最陡下降法会遭遇慢的收敛模式。这意味着如果能以某种方式消除特征值的分散特性，就则可以获得更好的收敛模式。一个随机过程x（n）称为是阶数M 的自回归AR（AutoRegressive）的差分方程来产生。

式中hi为AR 系数。而v（n）是一个零均值的白噪声过程，称为x（n）的新息，它们与之前的样本不相关。

采用一个阶数M′≥M 的预测器，可得

和

令

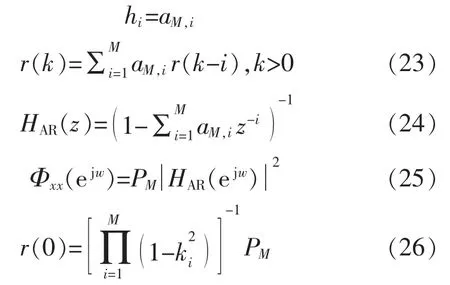
一个自适应横向滤波器输入过程的相关矩阵可由一个AR 过程来刻画，其阶数可能比自适应滤波器的阶数要小得多。

对于实值输入的自适应滤波器，LMSN 算法的递推方程为

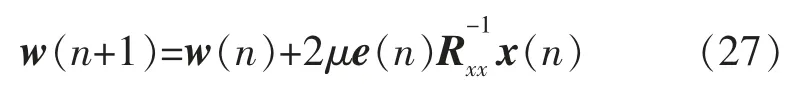
其中

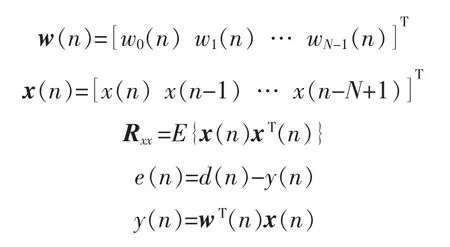
式中：w（n）为滤波器的实权值向量；x（n）为滤波输入向量；为输入自相关矩阵Rxx的估计；E｛.｝为统计平均； μ 为算法的步长；e（n）为滤波器输出的测量误差；d（n）为期望响应；y（n）为滤波器输出。

理想的LMSN 算法是一个不切实际的版本，首先假设Rxx是已知的，这在实际中是不可能实现的，但这是一个有用的算法，可用于分析LMSN 算法的拟合版本的预期性能。为了解决计算计算复杂度比较高的问题，输入序列x（n）被建模成M 阶的（M 远小于滤波器长度）自回归模型，结果表明该算法的计算复杂度与传统的LMS 算法相当。本文算法继承了LMS 算法的鲁棒性。

为了实现LMS Newton 算法，每次迭代更新都要计算采用传统的方法效率较低，有必要寻找其他解决方案。对此，提出了一种直接更新向量的方法，即将输入向量x（n）转换为其的后向预测误差，此外x（n）和b（n）的关系为

其中

式中：L 为预测因子系数，由下三角的矩阵构成；ai，j为第i 阶第j 个预测值。因此，b（n）中的元素互不相关，这意味着相关矩阵Rbb=E｛b（n）bT（n）｝是主对角矩阵，从而得到Rbb的逆矩阵。此外可以获得

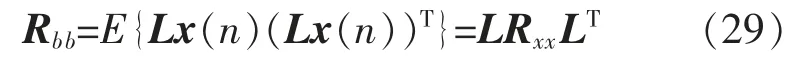
将式（29）取逆，且分别左乘LT，右乘L

再定义

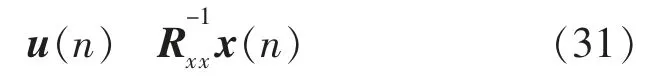
注意到

和

应用LMSN 算法来更新wE（n），此外由于原来的滤波器的抽头权向量对应于w0（n） … wN-1（n），wE（n）开头M 个和最后M 个元素固定为零，通过对这些权系数初始化为零并且分配零步长来完成。此时（其中L 和Rbb具有适当的维数）开头的M 个和最后的M 个元素的计算无关紧要。自适应滤波器抽头权向量更新方程式为

其中

式中：w（n）为所定义的滤波器抽头权向量。Rbb是一个与列向量L1xE（n）相一致的对角矩阵，且Rbb的对角元素是后者向量元素的功率估计。矩阵L1和L2

L1，L2的维数分别为（N+M）×（N+2M）和N×（N+M）。L1的行数仅为N，是因为在此无需要计算的前面M 个和最后M 个元素。

分析式（35）可见，每次ua（n）的更新只需要向量的第1 个元素，然后更新最后结果ua（n）的第1 个元素。2 个向量的其余元素是它们第1 个元素的时间延迟版本。将其整合在一起，图5 描述了修改版LMSN 算法的完整结构。图中，包含一个后向预测误差滤波器的HbM（z），利用一个自适应算法来更新其系数aM，i（n）。由后向预测误差滤波器的连续输出样本，即bM（n+M）乘以其能量估计值的倒数，表示为，给出的更新。

由接下来的滤波器对后续结果进行滤波，给出序列ua（n）（即其元素）的样本。该滤波器的系数是逆序排列的后向预测误差滤波器系数的复制。

图5 修改的LMSN 算法框图Fig.5 Modified LMSN algorithm block diagram

3 算法仿真与结果分析

3.1 主动噪声消除算法仿真

所提的ANC 系统在MatLab 2016b 进行仿真。为准确衡量在线辨识的收敛性能辨识的精确性，定义次级通路辨识误差ΔS/dB 为

为了直观地衡量系统的降噪性能，定义衡量标准为

R（n）值越大，则系统降噪量越大，反之亦然。

主路径和次级路径的试验数据使用文献[2]所提供的试验数据，得到P（z）和S（z）的实权值长度；控制滤波器W（z）和建模滤波器为长度分别为L=32，M=16 的实权值滤波器。

在Zhang 的方法中，第3 个自适应滤波器H（z）选择长度为16 的FIR 滤波器，Δ=16。在初始化的时候控制滤波器选为一组零向量w（0）。在Zhang 的方法中的第3 个自适应滤波器初始化选一组零向量h（0），LMSN 中重构阶数Q=2。

设仿真中初级通路的传递函数为

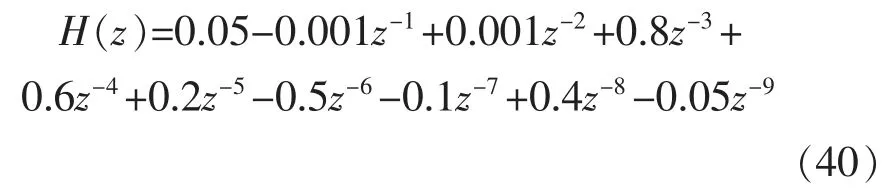
次级通路的传递函数设为

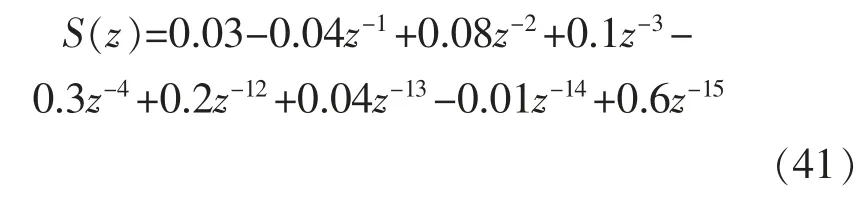
3.2 噪声信号控制算法仿真结果

在仿真过程中，分别针对Eriksson，Zhang 及本文改进算法进行2 种不同状态下的仿真。

3.2.1 输入噪声信号为高度有色化信号的仿真

为验证算法的性能，参考信号选用将方差为2的、零均值、信噪比为30 dB 的白噪声，通过色化滤波器H（z）产生。建模滤波器的激励信号v（n）选用方差为0.05，均值为0 的高斯白噪声。

Eriksson 算法设置uw=1×10-4，us=3×10-3；Zhang算法设置uw=3.5×10-4，us=4×10-3，uh=1×10-4；本文改进算法设置uw=5×10-4，us，max=1.25×10-2，us，min=4×10-4，uh=2×10-2。

将高斯白噪声通过自定义的传递函数F（z）后，可以使参考信号产生1000 以上的特征值分散度。

产生时域如图6 所示，功率谱密度如图7 所示。由图7 可见，输入信号的特征值分散度大到10000 的范围内。

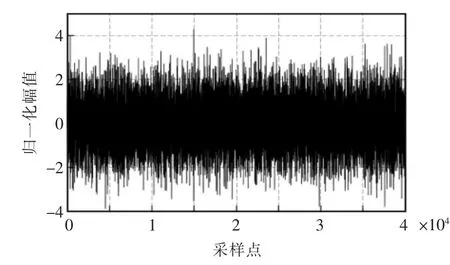
图6 输入噪声的的时域图Fig.6 Time domain plot of input noise

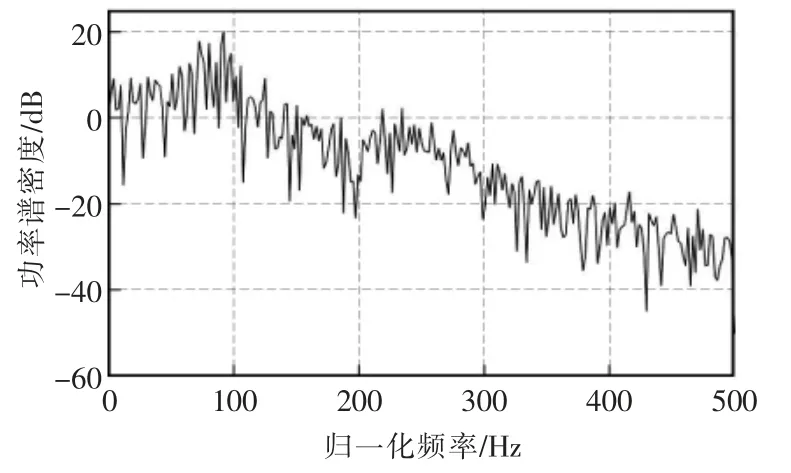
图7 输入噪声的功率谱密度Fig.7 Power spectral density of input noise

本文改进算法、Eriksson 和Zhang 的算法在降噪性能R（n）上的比较如图8 所示。由图可见，通过LMSN算法消除误差信号，改进算法表现出了更好的降噪效果。次级通道辨识误差的对比如图9 所示。由图可见，本文改进算法的ΔS（n）很快稳定下降至-40 dB，表明该方法可以加快建模滤波器的收敛速度。本文方法建模滤波器的步长us（n）如图10 所示。

图8 降噪效果R（n）对比Fig.8 Noise reduction effect R（n） contrast

图9 次级通道辨识误差Fig.9 Secondary channel identification error

图10 本文方法建模滤波器的步长us（n）Fig.10 Step size of the modeling filter us（n）

3.2.2 参考噪声为室内噪声信号

为验证算法的性能，参考噪声为室内噪声信号。建模滤波器的激励信号v（n）选用方差为0.00625，均值为0 的高斯白噪声。

产生时域如图11 所示，功率谱密度如图12 所示，从图12 可以看出，输入信号的特征值分散度大到10000 以上的范围内。

图11 输入噪声的的时域图Fig.11 Time domain plot of input noise

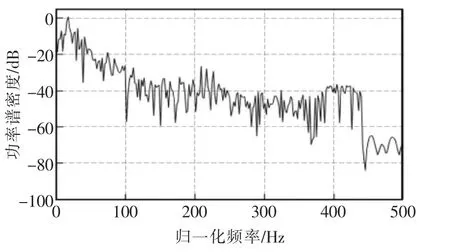
图12 输入噪声的功率谱密度Fig.12 Power spectral density of input noise

在室内噪声环境下，本文改进算法、Eriksson 和Zhang 的算法在降噪性能R（n）上的比较如图13 所示。由图可见，通过LMSN 算法消除误差信号，改进算法同样具有更好的降噪效果。次级通道辨识误差的对比如图14 所示。由图可见，在室内噪声环境下，ΔS（n）很快稳定下降到-40 dB，这说明改进算法可以加快建模滤波器的收敛速度。本文方法建模滤波器的步长us（n）如图15 所示。

图13 降噪效果R（n）对比Fig.13 Noise reduction effect R（n） contrast

图14 次级通道辨识误差Fig.14 Secondary channel identification error

图15 本文方法建模滤波器的步长us（n）Fig.15 Step size of the modeling filter us（n）

4 结语

提出了一种基于次级通道在线辨识新算法交叉更新有源噪声控制系统，将其应用到室内噪声消除中，通过分析该算法可以消除主动控制环节和次级通道建模环节的相互影响，提高整个ANC 系统的收敛速度和降噪行性能，并结合单通道前馈有源ANC 系统对其进行了性能仿真。仿真结果表明，与现有方法相比，所提方法对ANC 系统具有更好的降噪性能和对次级通道具有更精确的建模精度以及更快的收敛速率。