基于PSO-SVM 的电涡流传感器温度补偿的研究

潘 杰，卢文科，冯 阳，左 锋

（东华大学 信息科学与技术学院，上海201620）

电涡流传感器是用可产生“涡流效应”的金属导体作为核心元器件的传感器，它可以将震动频率和位移等物理量转换成电信号输出。该装置结构简单，线性范围好，灵敏度高，适用性强，方便非接触性测量，不损伤被测量工价的表面。该传感器主要由导线和被测导体组成，因此线圈阻抗的大小和被测导体的电导率和磁导率都对温度比较敏感，尤其在高温情况下会存在严重的误差，产生温度漂移，使测量结果发生严重偏差。为了减小影响，需要进行温度补偿[1]。传统方法是通过硬件电路的补偿，这种方法电路设计难度较大，精度不足，可移植性差，无法满足现代设计需求。在此，采用改进群粒子支持向量机的算法，对测量结果进行修正，消除传感器的交叉敏感，对温度进行较好的补偿[2]。

1 电涡流传感器的工作原理

电涡流传感器的结构如图1 所示。线圈提供可变电流I1，产生可变磁场H1，金属导体就会产生旋涡状感应电流I2，两者的相对位置不同导体会产生不同的反向交变磁场H2，改变线圈的有效阻值，从而改变电信号输出[3-4]。

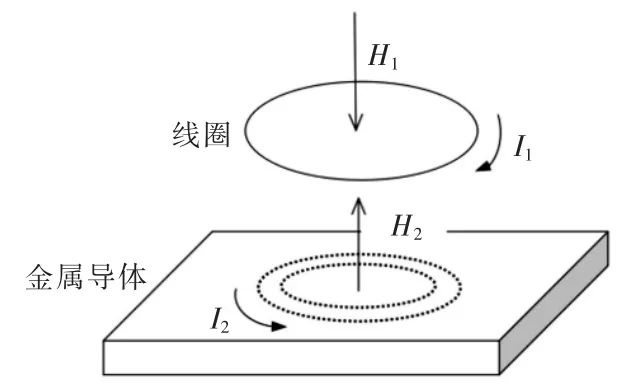
图1 电涡流原理示意图Fig.1 Schematic diagram of eddy current principle

为便于分析，图1 的等效电路如图2 所示。图中，左侧是通电线圈在高频的阻值R1和等效电感L1；中间是线圈和导体靠近时产生的互感M，它会依据两者之间相对距离的变化而反向改变；右侧是被测导体的等效电阻R2和等效电感L2。

图2 电涡流传感器等效电路Fig.2 Eddy current sensor equivalent circuit

由电路原理基本定理，得到：

则线圈的等效阻抗为

由式（4）可知，当其他参数保持不变时，线圈阻抗仅与互感M 有关，而M 的取值受线圈与金属导体相对距离S 的共同影响。但是在实际应用中，线圈阻抗受到周围温度干扰较大，极易产生偏差，需要对其进行温度补偿。

2 PSO-SVM 矫正原理

2.1 支持向量机的原理

支持向量机SVM（support vector machine）是一种新的机器学习方法，以统计学习理论（statistical learning theory）为基础，采用了结构风险最小准则，提高泛化水平，找寻最优解，能够很好地解决容量小和非线性的问题[5-6]。

其中支持向量机结构如图3 所示。图中，ai（i=1，2，3，…，s）为拉格朗日乘子，用于转换成对偶问题；K（x，xi′）为核函数，用于不同维度之间的映射；x 为检验样本或实测样本中的某个向量；xi′（i=1，2，3，…，s）为支持向量；y（x）为x 的输出量。

图3 支持向量机的结构Fig.3 SVM structure

图中，由初始观测样本构成输入空间，利用某种关系把低维空间的数据反映到高维空间。用于数据拟合的线性回归函数为

给定的样本数据集为

最优化回归函数[7-8]通过最小化以下的泛函式获得：

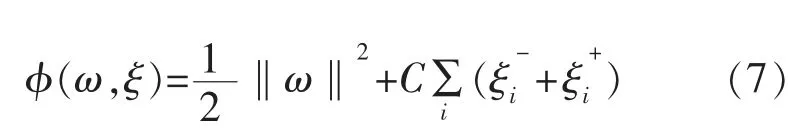
约束条件为

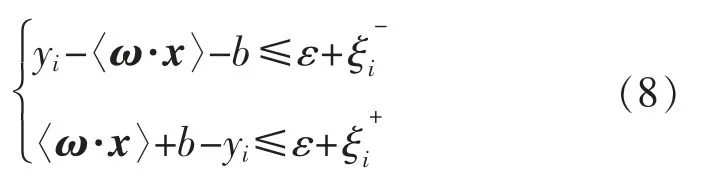
式中：C 为惩罚因子，是需要初始化的预定值，用于控制样本拟合能力和预测能力；ε 为不敏感损失函数系数，用于减小目标偏差，提升回归精度为松弛变量，分别为约束的上界和下界。

支持向量机通过对偶表达避免高维空间之中复杂的计算影响，通过K（x，xi′）的值来得到内积，从而有效避免维数灾难[9]。在此所采用的核函数是高斯型径向基函数RBF，表达式为

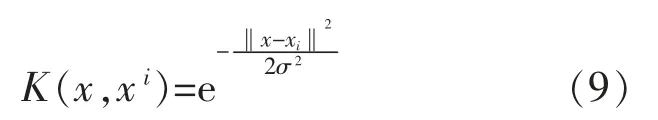
模型中的2 个参数——惩罚因子C 和核函数参数σ ——需要自行选取，在此采用粒子群算法寻优来找到最合适的参数大小。

2.2 粒子群算法

粒子群优化POS（particle swarm optimization），是一种群智能研究领域的算法[10-11]，源于对鸟群习性的仿真研究，在19 世纪90 年代正式诞生。该算法模仿生物群体在寻找目标的进程中展现的寻优方案，仅需运用一些基础数学计算，易于实现。在此用于优化参数得到最优解。粒子群迭代的公式为

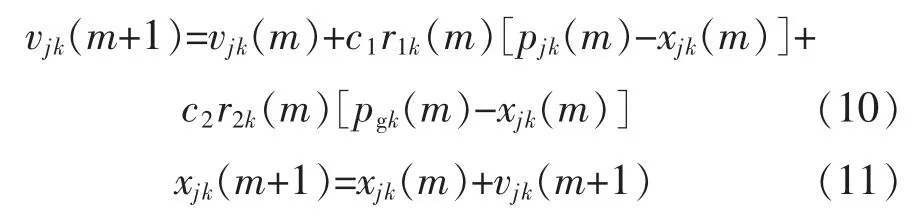
式中：vjk（m），xjk（m）分别为m 次迭代后第j 个粒子在空间k 维的位置和速度；c1和c2为加速因子，c1为认知参数，c2为社会参数；r1k，r2k为［0，1］区间的随机函数；pjk（m）和pgk（m）分别为单个粒子j 和全部粒子在m 次迭代后的历史最优解。式（10）是将单个粒子的m 次迭代后的位置和历史最佳位置做差，然后进行随机化，再将整体的最优位置和粒子m 次迭代后在空间k 维位置做差，进行随机化，两者的和作为下一时刻速度vjk（m+1）的调整分量。

在粒子群移动迭代的进程中，必须对单个粒子进行适应值计算，其中的适应度是用于判断单个粒子位置是否代表群体最佳的工具。

假定，f（x）为最优化目标，其确定的最好位置为

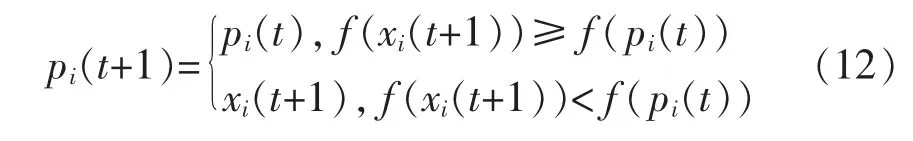
算法结束的条件是：迭代次数超过预定值或者代入群体最佳位置得到的是最好适应值。此时粒子群的最好解代表的适应度函数是历史最佳。

2.3 PSO-SVM 模型实现

PSO-SVM 模型的算法流程如图4 所示。

图4 PSO-SVM 流程Fig.4 PSO-SVM flow chart

将粒子群和支持向量机融合[12]，通过建立回归预测模型，其中惩罚因子C 和核函数参数σ 对向量机预测结果有较为重大的影响，利用粒子群算法优化参数，首先确定好迭代次数、加速因子c1和c2，设定一个粒子群的初始速度和初始位置，通过粒子群计算出每次迭代改善的C 和σ 的值，接着将两者代入向量机开始训练试验数据，求出预测值，并且将预测值和期望值的方差结果设置为适应度大小。对于每一个粒子，修改其最好位置pjk的条件是适应度相较于历史最佳点更优； 更新全局最好pgk的条件是在粒子优化过程中，群体的适应值小于历史最小的点。当迭代进程超过初始值，此刻的参数值最佳，代入C 和σ 求出预测值，此时便是误差补偿的结果。

3 电涡流传感器的温度补偿

在PSO-SVM 的温度补偿系统中，如图5 所示，通过改变被测导体和线圈的相对距离S 可以调整US，改变周围温度T 可以改变温度传感器的测试电压UT，再将两者通过PSO-SVM 算法模块拟合数据，使电涡流的电压输出端有一个S*，最终实现温度补偿的效果。

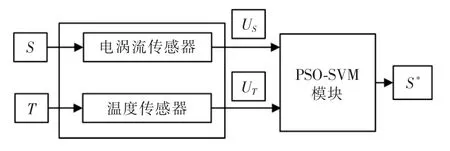
图5 PSO-SVM 温度补偿系统框图Fig.5 Block diagram of PSO-SVM temperature compensation system

3.1 二维定标试验

在一定工作范围内，将传感器按照试验要求放置恒温箱，在不同工作环境温度下，按照电路图连接电路，调整相对距离S，以0.2 mm 为间隔，记录不同位移下电路的输出电压值。在不同温度下重复上述操作，所记录的数据见表1。

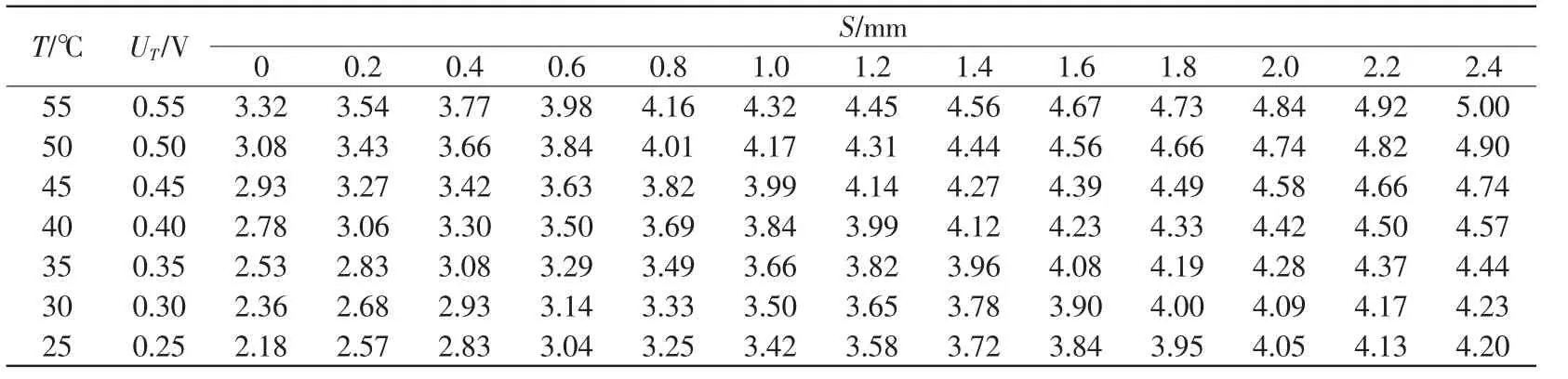
表1 不同温度下电涡流传感器的静态标定数据（US/V）Tab.1 Static data of eddy current sensors at different temperatures（US/V）

根据二维试验所测量邮的物理量，绘制出该传感器相对距离S 和测量电压US的特征关系曲线，如图6 所示。由图可见随着温度的改变，特性曲线发生温度漂移，其非线性度也很大。

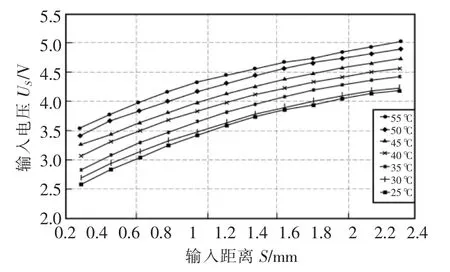
图6 补偿前的输入输出特性曲线Fig.6 Input-output characteristic curvesbefore compensation

根据表1 数据，可以求出以下温度系数：

①零位温度系数α0

其中

式中：ΔU0max为相对距离S=0 时不同温度所导致的电压最大偏移值，V，在此为3.32 V-2.18 V=2.025 V；U（FS）为电涡流传感器的量程，V，在此为5 V-2.18 V=2.82 V；ΔT 为温度的测量范围，℃，在此为55 ℃-25 ℃=30 ℃。

②灵敏度温度系数αs

式中：U（T2）-U（T1）为在某个特定的相对距离S 条件下由于不同温度所导致的电压最大偏移值，V，在此为3.32 V-2.18 V=2.025 V；U（FS）为该电涡流传感器的量程，V，在此为5 V-2.18 V=2.82 V；ΔT 为温度的测量范围，℃，在此为55 ℃-25 ℃=30 ℃。

3.2 PSO-SVM 算法温度补偿模型分析

使用粒子群优化支持向量机参数算法时，选用试验中的5 组测量值作为训练样本，另外2 组测量值作为测试样本。

开始运算前，设定粒子总数为30，更迭总数为300，此时的补偿效果较为明显；加速因子c1=1.8，c2=1.2，两者可保障较好的全局性，对试验中的测量物理量US和UT进行归一化，然后开始优化训练。

所预测的相对位移S*即温度补偿效果见表2。

根据表2，得到零位温度系数为

表2 PSO-SVM 补偿后的输出值（S*/mm）Tab.2 Output values after PSO-SVM compensation（S*/mm）

把式（13）和式（14）与式（15）和式（16）做对比（即图6 与图7 做对比），由图可见，电涡流传感器在数据融合后，其零点温度系数优化效果上升近2个精度，而灵敏度温度系数优化效果上升1 个精度，极大地改善了温度漂移带来的问题。

图7 电涡流传感器温补后的输出特性曲线Fig.7 Output characteristic curves of eddy current sensor after temperature compensation

4 结语

针对电涡流传感器数据因温度变化产生漂移的现象，提出了利用粒子群算法优化向量机的软件矫正方法进行温度补偿。其中粒子群主要优化向量机2 个参数——惩罚因子C 和核函数σ；将优化后的参数代入模型，求出预测值。试验证明，在数据融合后，灵敏度温度系数由1.35×10-2/℃提升至5.59×10-4/℃，优化效果提升近2 个精度；零位温度系数由1.35×10-2/℃提升到1.81×10-4/℃，优化效果提升1 个精度。