金属膜片充压翻转的动态仿真方法研究

宋冠华，周仕明，李道奎

(国防科技大学 空天科学学院，湖南长沙 410073)

0 引言

推进剂贮箱作为航天器的重要组成部分，具有管理控制推进剂的功能[1]。金属隔膜贮箱因具有工作原理简单、可靠性高、排空效率高,以及不受干扰加速度影响等特点，而被广泛应用于需要频繁调姿、经常变轨的航天器。此外，金属隔膜贮箱具有强度高、耐腐蚀性好、变形过程可控、抗渗透性好等特点，可解决液体燃料晃动、精确控制和长期贮存的难题，显著提高航天器的寿命和机动性，具有广阔的应用前景[2]。

金属隔膜贮箱工作时，增压气体挤压膜片，将推进剂输送到管路，其间膜片经历了从上半球翻转到下半球的弹塑性大变形过程，工作原理如图1所示。金属膜片在翻转过程中易产生褶皱、偏心、破裂等缺陷，进而导致翻转失效[3]。金属膜片的翻转特性直接影响到整个航天器能否正常运行。因此，对其翻转规律及失效原因进行系统的研究是非常必要的。对于金属膜片翻转过程的研究，试验费用过于昂贵，尚未有好的解决方法，因此利用有限元法进行数值模拟是一种有效途径。

图1 金属隔膜贮箱工作原理Fig.1 Operational principle of metal diaphragm tank

国内外学者对膜片翻转特性做了大量的研究工作。RADTKE等[4-5]利用翻转实验和数值模拟等手段，对金属膜片的结构设计，选材和制造工艺进行了研究。强洪夫等[6-7]采用数值手段，研究了径厚比和典型结构参数对锥柱形膜片翻转特性的影响。然而，现阶段对膜片翻转过程的仿真分析大多是在膜片上施加恒定的压力，然后采用弧长法进行计算[8-10]。这种方法的缺点是计算效率低，经常出现计算结果不收敛的问题。此外，该方法还将膜片翻转过程作为准静态过程处理。而实际的膜片翻转是一个动态过程，气瓶按一定流速向气腔内充气，当气腔内压强达到膜片翻转临界载荷时，膜片开始翻转；此后，气腔体积增大，气腔内气体的量也不断增加，气腔内压强随时间变化。

本文采用ABAQUS有限元软件建立了金属膜片充压翻转的流固耦合有限元模型，采用显式动态分析法进行计算。气腔中气体的量、气腔体积和压强是随时间变化的量。该方法可更好地模拟膜片真实翻转的整个过程，解决了现有方法存在的计算收敛性差、计算效率低等问题，为金属膜片的设计提供了一种重要的仿真手段。

1 仿真方法介绍

1.1 弧长法

膜片翻转过程属于薄壳结构产生大变形的力学问题，涉及材料非线性、几何非线性的耦合[11]。传统的非线性平衡方程的求解方法包括Newton-Raphson法、修正的Newton-Raphson法、Quasi-Newton法等。在求解非线性屈曲问题时，当载荷增加至临界载荷，由于结构的切线刚度K逼近于零，求解会非常困难，因此很难得到收敛解，求解式为

(1)

WEMPNER和RIKS提出的弧长法，经过CRISFIELD，RAMN，FORDE等人的修正和完善，可用于非线性屈曲极值点附近的分析，通过追踪整个翻转过程中实际载荷、位移关系，获得全部状态信息[12]。当载荷参数为λk时，位移xk已知；当载荷参数增量为Δλk时，相应的位移增量为Δxk，则

ψ(xk+Δxk,λk+Δλk)=0

(2)

式中：Δxk和Δλk均是未知的，需要补充一个附加条件，即

f(Δxk,Δλk)=Δlk

(3)

式中：Δlk为增量弧长。联立求解式(2)，(3)可求得既满足平衡条件，又满足辅助方程的Δxk和Δλk。

弧长法是目前膜片翻转仿真分析中使用最多的方法，仿真结果与实验结果大致吻合[13-15]，但弧长法计算效率很低，即使构型合理的膜片有时也会出现计算不收敛的问题，且该方法还将膜片翻转过程近似作为准静态过程处理。因此，寻找一种计算效率高、收敛性好、能模拟膜片真实翻转过程的仿真分析方法是非常必要的。

1.2 显式分析方法

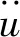
(4)

式中：P为所施加的外力；I为单元内力。

在当前增量步开始时(t时刻)，计算加速度为

(5)

采用中心差分法对加速度在时间上进行积分，用速度变化值加上前一个增量步中点的速度来确定当前增量步中点的速度，有

(6)

速度对时间的积分加上在增量步开始时的位移可确定增量步结束时的位移，有

(7)

在增量步开始时提供满足动力学平衡条件的加速度，然后在时间上“显式”前推速度和位移。为了使该方法的计算结果精确，时间增量必须足够小，这样在增量步中加速度几乎为常数。由于时间增量步很小，因此一个分析需要成千上万个增量步。但不必同时求解联立方程组，所以每一个增量步的计算成本很低，总体计算效率相对于弧长法有很大程度的提高。

显式分析法最显著的特点是不需要弧长法中所需的整体切线刚度矩阵。由于其为“显式”前推模型的状态，因此不需要迭代和收敛准则，不存在收敛性问题。另外，通过建立膜片流体腔流固耦合有限元模型，结合显式分析法，可真实模拟膜片充压翻转的过程。

2 有限元仿真分析

2.1 金属膜片充压翻转流固耦合有限元模型的建立

本文研究的膜片构型为锥柱形，包括下部预翻边(I部分)、锥线段(II部分)和上部圆弧段(III部分)，如图2所示。其中，锥线段与预翻边圆弧和顶部圆弧均为相切几何关系。

图2 锥柱形膜片结构Fig.2 Structure of cone-bar diaphragm

膜片几何参数如下：上部圆弧段半径R1为200 mm，锥线段长度L为20 mm，锥角α为78°，预翻边半径r为3 mm。膜片为变厚度分布，预翻边厚度为1.0 mm，锥线段最低点到膜片顶点，膜片厚度从1.0 mm到1.3 mm随高度线性变化。

整体有限元模型包括膜片和外层刚体，外层刚体与膜片围成气腔，如图3所示。图3(c)为整体有限元模型的1/2。膜片采用S4R壳单元，外层刚体采用R3D4单元，膜片材料为纯钛，此处看作理想弹塑形材料，弹性模量为113 GPa，泊松比为0.32，屈服极限为250 MPa，密度为4 500 kg/m3。气腔内的压强根据气腔内气体的量与气腔体积通过理想气体方程计算，采用显式分析法进行仿真分析。

图3 流固耦合有限元模型Fig.3 Fluid-solid coupling finite element model

2.2 流固耦合有限元模型的计算原理

气瓶以一定速度向气腔内充气，气腔压力逐渐增大。在气腔压力达到膜片翻转临界载荷之前，膜片主要发生弹性变形，膜片位移很小，气腔体积几乎不变，气腔压力随时间线性增加。当气腔压力达到膜片翻转临界载荷时，膜片开始翻转，此后气腔体积随着膜片翻转逐渐增大。此时，气腔中的压强为

(8)

式中：P(t)为气腔内气体压强；n(t)为气腔内气体的物质的量，n(t)=k·t，k为充压气体流速；R为理想气体常量；T为温度；V(t)为气腔体积，可通过膜片翻转过程中的节点坐标计算确定[17]。

在有限元分析中，显式动态分析采用时间增量步的方式。首先计算t时刻气腔内气体的量，并根据t时刻膜片和外层刚体的节点信息计算膜片和外层刚体围成气腔的体积，然后根据理想气体状态方程计算气腔内气体压强，给定时间增量Δt，最后计算膜片在气腔压力作用下在Δt时间增量内发生的位移，得到t+Δt时刻膜片节点信息，开始下个时间增量步的计算。图4为流固耦合有限元模型计算流程图。

2.3 显式动态分析法与弧长法仿真结果的对比

分别采用显式动态分析法和弧长法对图3中膜片进行翻转仿真分析，显式动态分析法采用流固耦合有限元模型，而弧长法采用单独的膜片有限元模型，通过在膜片上施加恒定压力载荷完成计算。将显式动态法与弧长法的分析结果进行对比，两种仿真分析方法计算得到的膜片翻转过程如图5，6所示。其中，U2表示膜片顶点轴向位移，显式动态分析中，充气速度为100 g/s。可以看出，膜片从预翻边处开始翻转，整个过程膜片未出现褶皱、凹坑，但都出现一定程度的偏心现象，两种仿真分析方法都能成功模拟膜片的整个翻转过程。

整个翻转过程中膜片翻转压差随膜片顶点轴向位移的变化关系如图7所示。两种方法计算得到的膜片翻转压差曲线基本重合，验证了显式动态分析仿真结果的合理性。

2.4 膜片翻转失效的动态仿真

建立与文献[3]中完全相同的膜片有限元模型和流体腔，膜片几何参数如下：上部圆弧段半径R1为384 mm，锥线段长度L为144 mm，锥角α为90°，预翻边半径r为14 mm。膜片为变厚度分布，预翻边厚度为2.0 mm，锥线段到膜片顶点膜片厚度从2.0 mm到3.5 mm随高度线性变化。膜片材料为铝，弹性模量为69 GPa，屈服强度为30 MPa，抗拉强度为70 MPa，延伸率为39%。采用显式动态分析法进行翻转仿真分析，得到膜片变形过程如图8所示。可以看出：0.3 s内，膜片正常向下翻转一段距离；0.4 s时，膜片在最下端出现屈曲现象；0.7 s时，膜片上出现大面积凹陷，翻转失效。

通过与文献[3]中实验结果进行对比，如图9所示，可以看出，显式动态仿真结果与实验结果基本吻合，膜片上均出现6个凹坑，屈曲模态相同。二者主要的区别是膜片变形的幅度不同，这可能是因为膜片在制造过程中存在几何缺陷，并且膜片在屈曲之后存在接触、挤压、摩擦等现象，而动态仿真中忽略了这些因素。由此得出，采用显式动态分析法能仿真出膜片翻转失效的整个过程，并且吻合度很高。

3 充气速度对膜片翻转特性的影响

图6 弧长法仿真结果Fig.6 Simulation result of arc length method

图7 膜片翻转压差曲线Fig.7 Relationship between differential pressure and top node axial displacement

膜片实际翻转过程与气瓶充气速度有关，为研究充气速度对膜片翻转特性的影响，分别以100， 200， 500， 1 000 g/s这4种充气速度，用显式动态分析法对图3中膜片进行翻转仿真分析。4种充气速度下膜片均成功完成翻转，未出现褶皱、凹坑。

图8 膜片翻转失效过程Fig.8 Failure process of diaphragm overturning

图9 动态仿真结果与实验结果Fig.9 Dynamic simulation result and experimental result

4种充气速度下，膜片翻转压差随膜片顶点轴向位移的变化关系如图10所示。可以看出：4种充气速度下膜片翻转压差曲线与弧长法计算得到的压差曲线基本吻合；唯一不同的是，显式动态分析法得到的压差曲线在中间翻转过程有一定程度的上下波动，并且充气速度越快，翻转压差波动的幅值越大，这一特点与膜片实际翻转过程相吻合。

膜片顶点横向位移可反映出膜片翻转过程中的偏心程度[18]，膜片翻转过程中顶点横向位移随顶点轴向位移的变化关系如图11所示。4种充气速度下膜片顶点最大横向位移分别为59，31，12，3 mm。可以看出：充气速度越快，膜片翻转过程中的偏心越小；1 000 g/s的充气速度下，膜片翻转过程如图12所示。与图5比较可发现，在1 000 g/s速度下，膜片翻转过程中基本无偏心。

图10 膜片翻转压差曲线Fig.10 Relationship between differential pressure and top node axial displacement

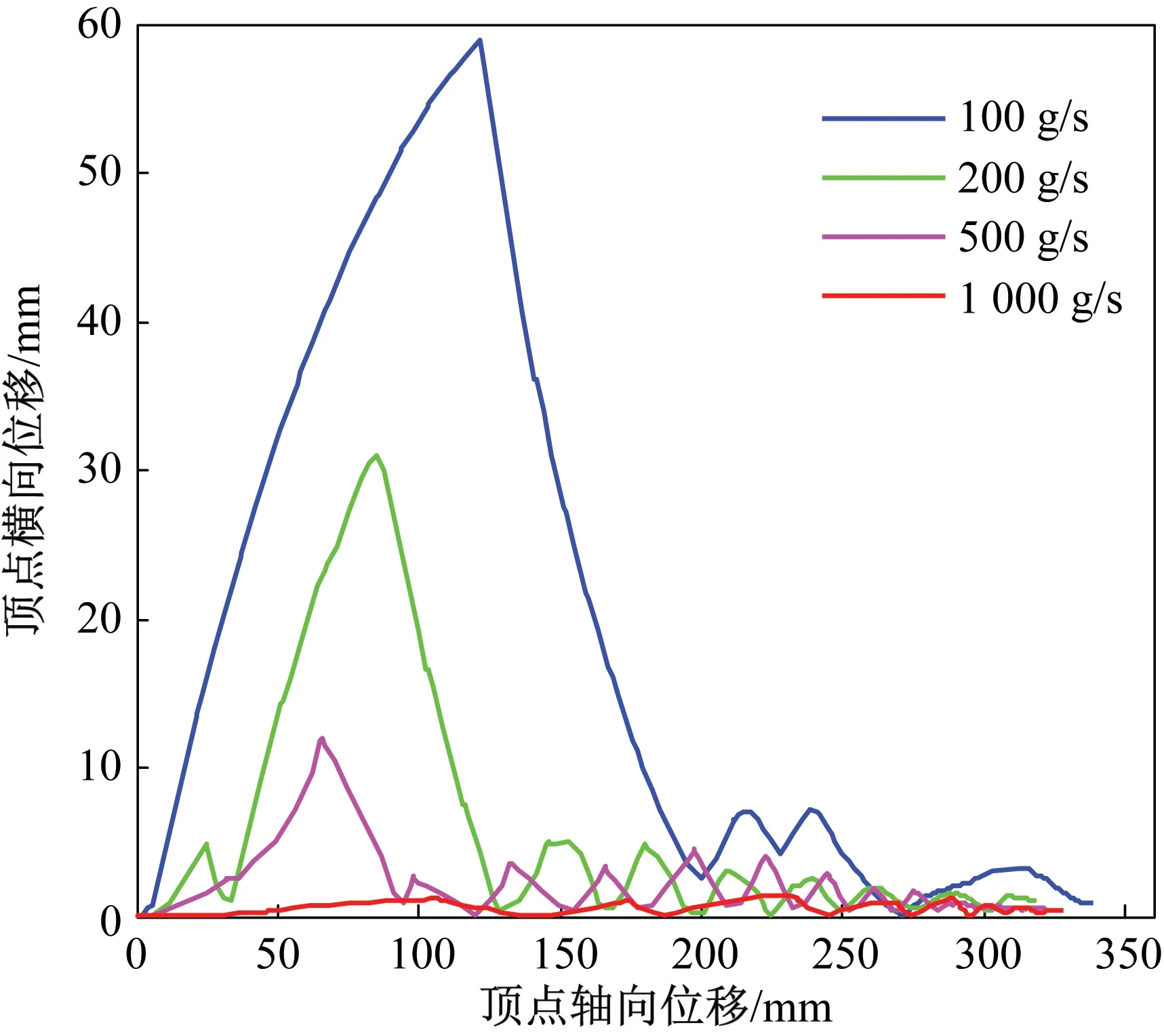
图11 膜片偏心程度Fig.11 Relationship between top node transversal displacement and top node axial displacement

图12 显式分析仿真结果(充气速度1 000 g/s)Fig.12 Simulation result of dynamic explicit method (Mass flux: 1 000 g/s)

4 结束语

本文建立膜片充压翻转的膜片流体腔流固耦合有限元模型进行显式动态仿真，通过与弧长法进行分析结果、实验结果的对比，验证了显式动态分析仿真结果的正确性；通过改变充气速度，研究了充气速度对膜片翻转过程的影响。主要结论如下：

1) 与弧长法相比，显式分析法计算效率更高，不存在收敛性问题。

2) 通过建立流固耦合有限元模型，采用显式动态分析法，将膜片翻转过程作为动态过程处理，气体按一定流速向气腔内充气，膜片上所受压力依赖于气腔体积和气腔内气体的量，这是随时间变化的量，与膜片实际的充压翻转过程更接近。

3) 膜片实际翻转过程受气瓶充气速度影响，通过建立流固耦合有限元模型，结合显式动态分析法，可以研究充气速度对膜片翻转特性的影响，得出不同充气速度下翻转压差曲线与偏心程度。

4) 充气速度越快，膜片中间平稳翻转过程的压力波动越大，偏心程度越小，这一特点与膜片实际翻转过程相吻合,而弧长法无法仿真出这一特点。

本文提出的显式动态分析方法法也可应用于球形、顶部凹陷形等其他类型的金属膜片翻转仿真，以及其他基于理想气体状态方程的有限元仿真分析。本文提出的仿真方法，可用于构型、几何参数、材料等对膜片翻转效果影响的研究，解决了目前仿真方法中存在的构型合理的膜片计算结果不收敛的问题，为金属膜片的优化设计提供了参考。