压力容器用拱形膜片液压胀形工艺的有限元模拟*

成鹏飞，孙嘉麟，许 岗,许军锋

(西安工业大学 材料与化工学院，西安 710021)

随着化学工业技术发展，各种化工生产中都需要用到压力容器，而在生产中压力容器往往长时间承受较高的压力，因此对它的安全性能提出了更高的要求[1-2]。爆破片作为压力容器的安全设施，对保障人员以及设备的安全至关重要[3-4]。爆破片作为一种一次性安全组件，相比于传统的安全阀具有密封性好，爆破动作无延迟，泄放面积大等优点，在压力容器以及压力管道等方面有广泛应用[5-6]。

压力容器爆破片可分为正拱形，反拱形和平板形[7]。其中正拱带槽形膜片具有爆破精准，无碎片等优点而有着广泛的应用[8-11]。常用正拱带槽型膜片的爆破压力主要由膜片厚度t0、拱高H以及刻槽深度h决定[8-9]，其中拱高是影响膜片爆破精度的重要因素[10]。拱形膜片的加工常用平板形膜片液压胀形法[11]。而液压胀形又分为模具液压胀形和无模具液压胀形。模具液压胀形的模具制造成本过高，而且板材与模具之间的摩擦力会影响膜片的成型。因此无模具液压胀形成为拱形膜片加工的主要手段[9]。同时，成型压力，不同的加载速度和夹具圆角等都会严重影响膜片成型[12-14]，工程上采用的试错法往往需要大量重复的试验，耗费人力物力。因此，采用有限元模拟方法确定成型工艺参数成为解决此类工程问题的有效手段[15-18]。

为了加工一种压力容器所用的不锈钢正拱带槽形膜片，本文针对膜片的液压胀形过程进行有限元模拟，主要探究了液压胀形工艺中的加载压力、加载速率、加载路径和夹具圆角等因素与膜片拱高的关系，为膜片的设计和加工提供参考。

1 研究方法

LS-DYNA是一种有限元模拟软件，在显式动力学分析中有广泛应用[19-20]。本文利用LS-DYNA进行模拟计算，研究膜片变形中非线性及大变形的模拟计算。

1.1 几何结构模型

膜片几何结构如图1所示，其中t0为膜片厚度，h为刻槽深度，b为槽宽，d为泄放口直径，D为膜片外径。模型尺寸见表1。考虑轴对称型，建立液压胀形膜片以及夹具的1/4模型如图2所示。

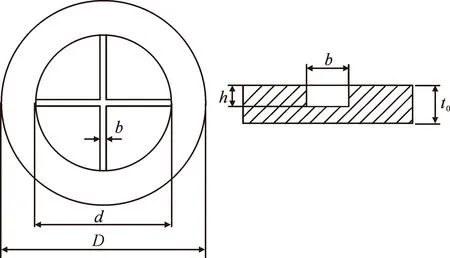
图1 膜片几何结构 Fig.1 Geometry of the diaphragm

表1 膜片结构参数Tab.1 Structural parameters of the diaphragm

图2 模拟加载模型Fig.2 Simulation model

1.2 材料参数

本文选用316L不锈钢板，通过ETM205D 型拉伸机进行拉伸试验，测得该板材在室温下的应力应变曲线如图3所示，模型材料选用“*MAT_PLASTIC_KINEMATIC”命令，其参数设置见表2。

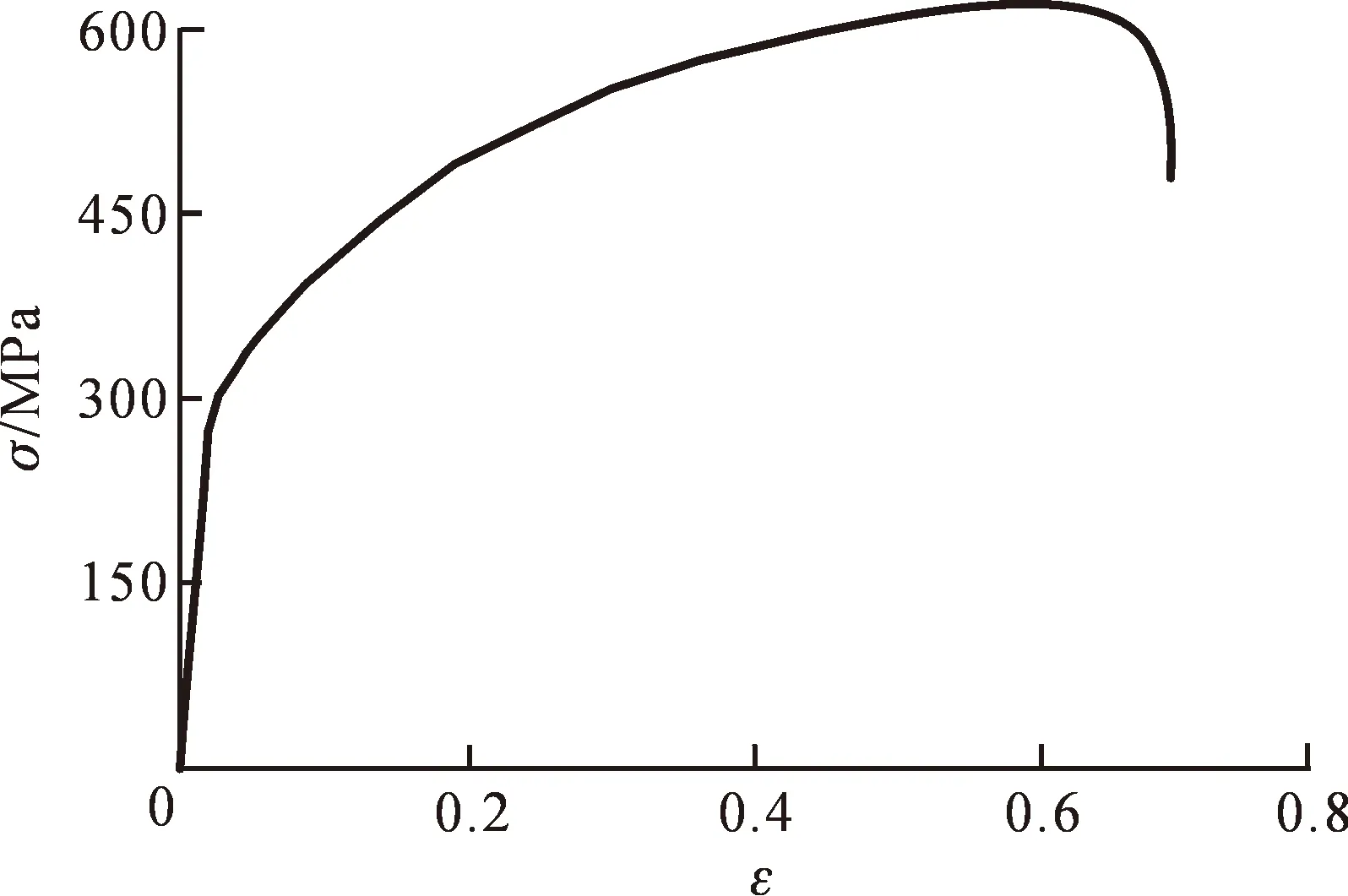
图3 316L不锈钢应力应变曲线Fig.3 The stress vs.strain curve of stainless steel 316L

表2 材料参数Tab.2 Material parameters

1.3载荷以及约束设置

建立上下夹具，模拟膜片在预拱成型过程中的加载面如图4所示，在夹具内侧范围内施加表面载荷，模拟液压胀形过程中液体对膜片表面的作用力。随着载荷的增加，膜片会向泄放侧隆起，形成拱面。

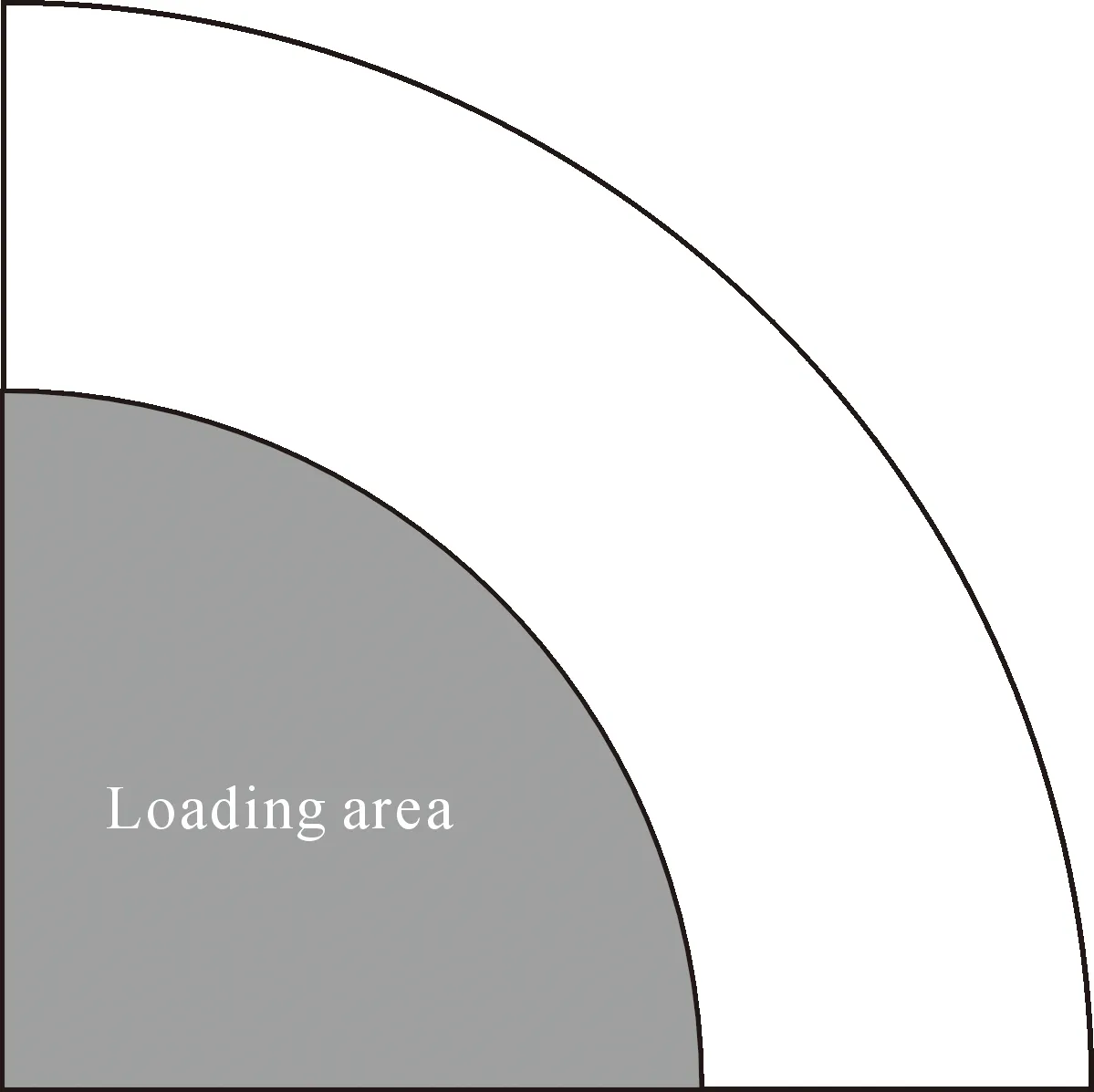
图4 加载区域示意图Fig.4 Schematic diagram of the loading area

2 结果与分析

2.1 加载压力与拱高的关系

在工程上，对于一种新的膜片结构制定液压胀形工艺时会进行多次试验，确定对应拱高H的膜片所需的加载压力P。采用有限元方法，设定不同的P对膜片胀形过程进行模拟，胀形后的模型如图5所示，得到P与H的关系如图6所示。图中可以看出，随着P的增加，膜片的H线性增加，其关系可以表示为

图5 胀形后模型Fig.5 Model after simulation experiment

H=K·P。

(1)

式中:H为胀形后拱高；P为加载压力;K为经验系数，通过图6曲线拟合得出K=0.421 1。

图6 H与P的关系Fig.6 Relation between arch height and pressure

膜片在胀形过程中随着P的增加，内部等效应力也随之增加。工程上普遍认为膜片最大等效应力等于材料抗拉强度σb时的加载压力为极限压力Pmax，而膜片最佳成型压力为Pmax的80%[20]。模拟过程中P与膜片内部等效应力关系如图7所示。本文所用的膜片材料为316L不锈钢，σb为621 MPa。因此由图7可知，当膜片等效应力等于材料σb时，其加载压力P为6.25 MPa，进而其最佳成型压力为5 MPa。

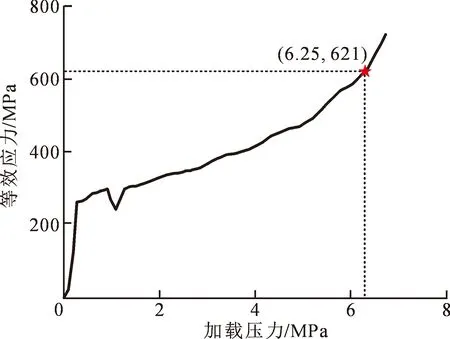
图7 膜片等效应力与P的关系Fig.7 Relationship between equivalent stress and pressure

2.2 加载速度与拱高的关系

图8表示加载压力以不同速度上升至最佳成型压力(5 MPa)时的加载速度曲线，其中A升压速度最快，为2.50 MPa·ms-1，E升压速度最慢为0.05 MPa·ms-1。按照不同的加载速度曲线对膜片进行胀形模拟，得到的加载速度与H的关系如图9所示。从图9中可以看出，H随着加载速度的降低而略有减小。这是由于加载速度低，金属在受力时能够充分变形，拱面变形更均匀，从而有更大的变形量[21]。且图9中H随加压速度曲线变化可知，在速度低于0.05 MPa·ms-1后，H趋于稳定。

图8 加载时程曲线Fig.8 Loading time history curves loading speed curves

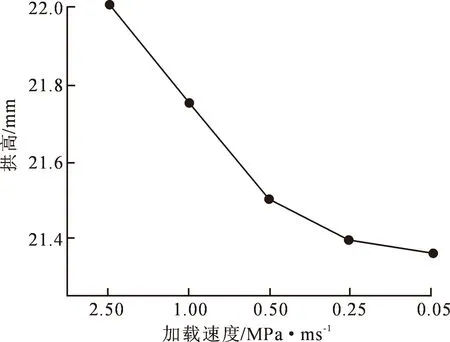
图9 H与加载速度的关系Fig.9 Relation between arch height and loading speed

2.3 加载路径与拱高的关系

研究表明，膜片成型过程中存在最佳成型曲线，即加载速度变化对H精度影响较大[9]。本节讨论了三种加载速率路径，如图10所示。在0～4 ms内Path 2上升最快，Path 3上升最慢；在4～10 ms内Path 2上升最慢，Path 3上升最快。对H的影响如图11所示，对比可知，Path 2的拱高最小，Path 3的拱高最大。在胀形过程中的变速加压会导致不同的拱高，这与金属受力时的力学行为有关[21]。加载初速低，金属在受力时能够充分塑性变形，拱面变形更均匀，从而有更大变形量[22]；后续的高速加载使得变形更加充分稳定，形成最大的拱高。加载初速高，金属受力后发生弹性形变，进而增大变形过程中金属的疲劳强度和蠕变强度[21]，导致变形不充分；后续低速加载造成的变形量有可能不足以抵消降速后金属弹性释放量，因此不能获得理想的拱高。因此，膜片拱高的设计应当考虑加压速率的变化。

图10 加载路径曲线Fig.10 Loading path curves

图11 不同加载路径的拱高Fig.11 Arch heights of different load paths

2.4 夹具圆角与拱高的关系

在膜片胀形过程中，膜片在夹持部位边缘会受到较大的剪切作用。为了避免在夹持部位出现剪切断裂，在泄放口的夹具内沿会加工一定半径R的圆角，如图12所示。模拟了不同夹具圆角半径(R=0.0～15.0 mm)的模型模拟胀形后的H如图13所示。可以看出，随R的增大，胀形后H有所增加。这是由于R增加有利于夹持部位边缘金属的流动，从而可以有较大的H。图14所示为不同R时胀形过程中膜片中心和边缘最大剪切应力变化曲线。可以看出，R<1.5 mm时，膜片边缘的剪切应力大于膜片中心位置；随R增加，膜片边缘区域的最大剪切应力明显降低，这源自于圆角的存在有助于夹持部位边缘金属的流动，使膜片变形均匀，降低边缘剪切断裂的风险。同时当R>1.50 mm时，膜片边缘的剪切应力小于膜片中心位置；当R>5 mm后，随R增大边缘剪切应力减小缓慢，并趋于稳定，因此R为1.5～5.0 mm可以有效避免膜片夹持部位剪切断裂，此时圆角半径R是厚度t0的3～10倍，为R模拟的最佳取值范围。

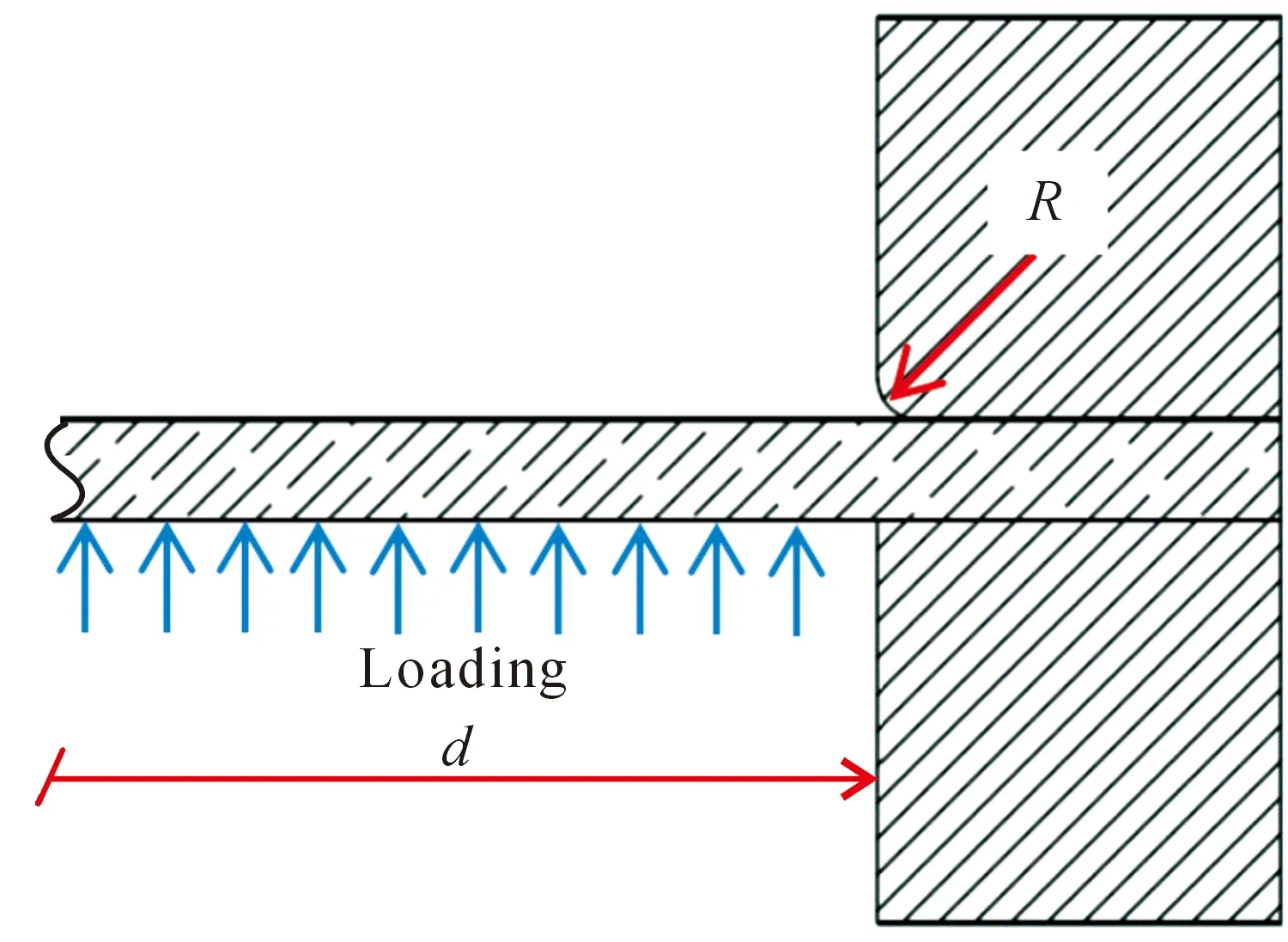
图12 夹具圆角Fig.12 Schematic diagram of the fixture

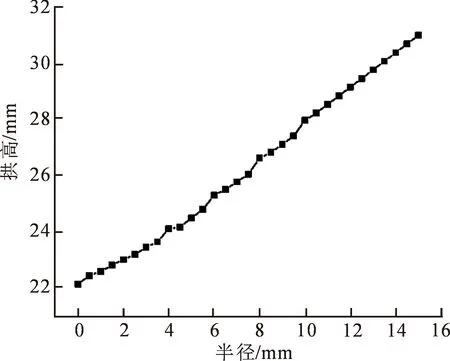
图13 H与R的关系Fig.13 Relation between arch height and fillet radius

图14 R对膜片不同位置剪切应力的影响Fig.14 Relation between shear stress and fillet radius

然而在工程中，随R增大拱起位置与膜片中心距离L增加，过大的R会导致膜片变形区域增加，无法满足压力容器的密封对接需求，如图15所示。因此实际工况下安装膜片的夹具圆角R多设定为膜片厚度t0的3～4倍[12]。综上所述，对于泄放口径d=100 mm，厚度t0=0.5 mm的膜片，其圆角半径R应该控制在1.5～2.0 mm。

图15 R对膜片变形范围的影响Fig.15 Influence of fillet radius on the deformation range of the diaphragm

3 结 论

通过对一种压力容器中正拱带槽型膜片的胀形过程进行有限元模拟，研究了胀形过程中加载压力、加载速度、加载路径、夹具圆角等对胀形后拱高的影响规律，得出以下结论：

1) 加载压力对膜片胀形拱高起决定性作用，本文采用的膜片最佳成型压力为5 MPa。膜片其拱高和加载压力的关系可以表示为H=K·P。

2) 随着加压速度的降低，膜片变形更加均匀，模型的拱高略有减小，在加载速度低于0.05 MPa·ms-1后，拱高趋于稳定。

3) 加压速率变化会导致膜片成型尺寸偏离设计尺寸。实际加工中应考虑加压速率变化方式。

4) 随着夹持圆角半径增加，拱高线性增加，且夹持部位边缘的剪切应力有所下降，但过大的圆角会导致变形范围增大。对应于直径为100 mm，厚度为0.5 mm的膜片，其圆角半径为应该控制在1.5～2.0 mm。