捆绑火箭POGO振动动力学模型的研究

周星光，孙 冰，翟师慧，汤 杰

(1. 上海航天精密机械研究所，上海 201600； 2. 北京航空航天大学 宇航学院，北京 100083)

0 引言

POGO振动是指液体火箭结构系统与推进系统相互耦合而产生的纵向不稳定振动，在低频振动中占有不可忽视的地位[1]。POGO振动不仅损害航天器自身的功能及设施，还会严重威胁宇航员的生命健康[2-3]。因此，POGO振动的抑制对于液体火箭的设计非常重要。

如今对POGO振动的研究众多，但研究模型大多数是单组元模型或者是没有考虑耦合的双组元模型[4-11]，对液体捆绑火箭的POGO振动分析较少。文献[12]中给出了单组元模型中蓄压器的最佳设置位置，但未分析捆绑火箭模型。文献[13]中给出了火箭飞行过程中各部件产生的作用力，但未分析这些作用力对POGO振动的影响程度。

POGO 振动稳定性方法有许多种，但其实质都是一样的，即特征方程根的实部为负时，系统是稳定的；否则是不稳定的。系统阻尼比为特征方程根的实部与系统特征频率的比值，则液体捆绑火箭 POGO振动仿真模型的稳定性条件变为：如果系统阻尼比为正，则系统是稳定的；如果为负，则系统失稳。本文搭建了液体捆绑火箭动力学仿真模型，分析了蓄压器的位置对捆绑火箭POGO振动抑制效果的影响，以及各个部件处产生的作用力对捆绑火箭POGO振动的影响。

1 设计思路

通过Rubin[13]模型，考虑了助推段与芯级之间的耦合关系，搭建了双组元液体捆绑火箭动力学仿真模型。在捆绑火箭中，蓄压器可抑制POGO振动，但其安装方式共有15种。通过调整蓄压器的位置，分析火箭飞行过程中泵、贮箱、直管、推力室处产生的作用力对POGO振动的影响程度，来简化液体捆绑火箭POGO振动动力学模型。

2 液体捆绑火箭动力学模型的建立

参考文献[13]中贮箱、波纹管、直管、蓄压器、泵、推力室等部件的动力学方程，以及贮箱、直管、泵、推力室产生的作用力动力学方程，基于AMESim建模软件的二次开发平台AMESet，构建液体捆绑火箭推进系统的贮箱、波纹管、直管、蓄压器、泵、推力室等部件模块。

捆绑火箭的POGO耦合系统由氧路的耦合系统和燃料路的耦合系统组成，以氧路的耦合系统为例，如图 1 所示。

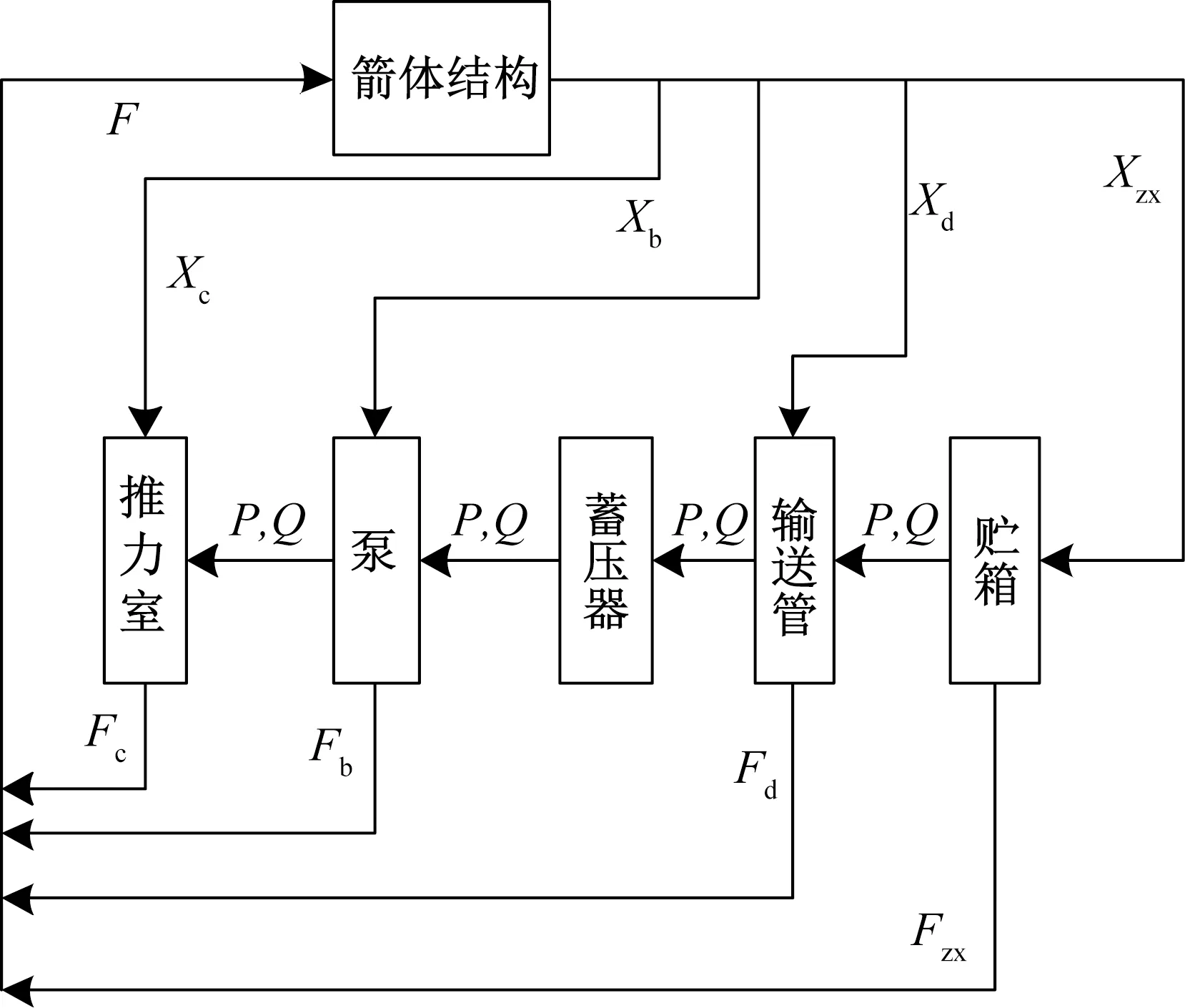
图1 氧路耦合系统Fig.1 Oxygen circuit coupling system

图1中各部件之间通过脉动压力(P)和脉动流量(Q)相互联系。图中：vc，vb，vd和vzx分别表示箭体结构在推力室、泵、直管、贮箱处反馈回来的纵向振动速度；Fc，Fb，Fd和Fzx分别表示推力室、泵、直管、贮箱处产生的作用力。

在贮箱处产生的作用力

(1)

式中：Qzx为贮箱处的脉动流量；β为单位面积上的脉动压力；ρ为推进剂的密度；Pzx为贮箱处的脉动压力；Azx为贮箱的横截面积；Nzx为贮箱处的模态参数。

在直管处产生的作用力

(2)

在泵处产生的作用力

Fb=PbiAbiNbi-PboAboNbo+

(3)

式中：Pbi，Pbo为泵入口和出口处的脉动压力；Abi，Abo为泵入口和出口处的横截面积；Nbi，Nbo为泵入口和出口处的模态参数；Ws为稳态流量；Qbo为泵出口处的脉动流量。

在推力室处产生的作用力

Fc=-AtCfPcNc

(4)

式中：At为推力室的喉部面积；Cf为推力系数；Pc为推力室内的压力；Nc为推力室的模态参数。

在广义坐标系下描述箭体结构纵向振动的方程为

(5)

式中：Mi，Ci，Ki，φi分别为第i阶模态质量、阻尼、刚度和振型列阵；Fi为第i阶广义力。根据式(5)，在AMESet中完成液体捆绑火箭结构系统模块的构建。芯级和助推器参数见表1，捆绑火箭的纵向模态参数见表2。

在此基础上，引入贮箱、直管、泵和推力室的纵向振动速度和加速度信号反馈，参考文献[12]中的蓄压器在单组元模型中的最佳位置，在AMESim中搭建了液体捆绑火箭动力学仿真模型，如图2所示。

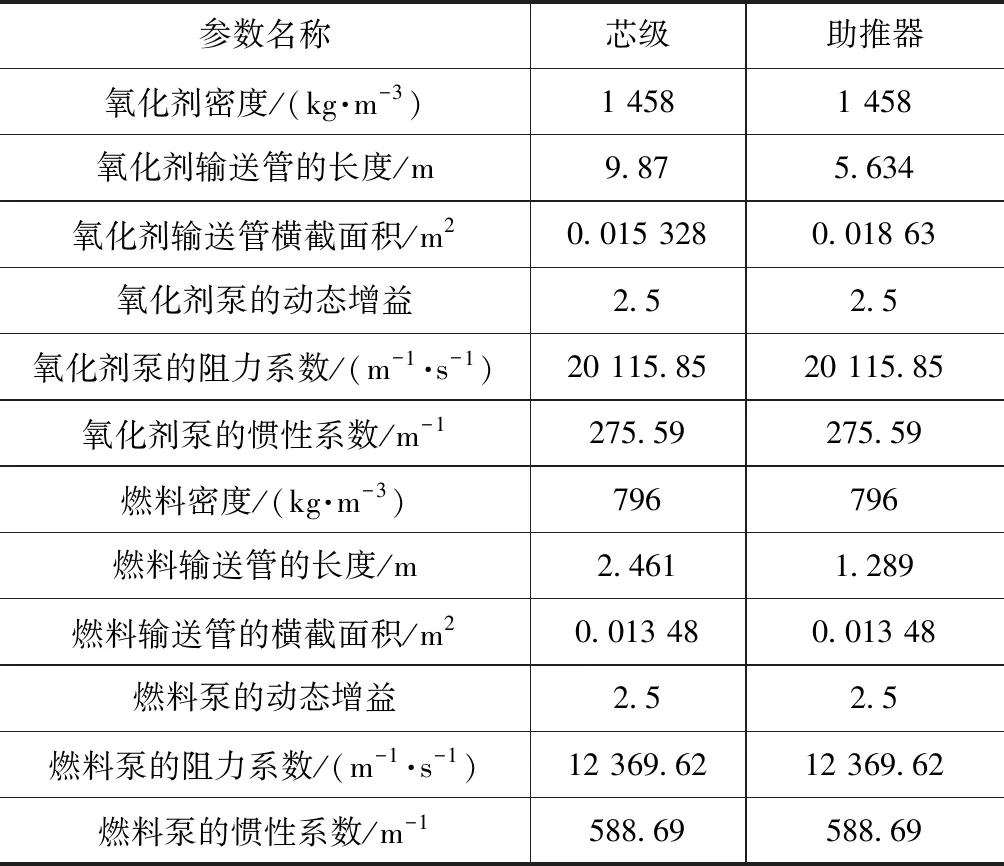
表1 芯级和助推器参数

表2 捆绑火箭的纵向模态参数

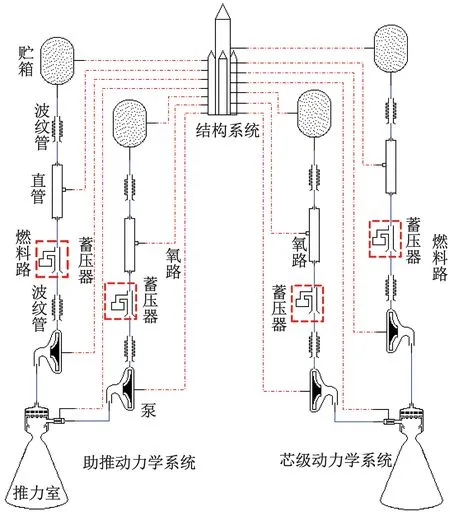
图2 液体捆绑火箭动力学模型Fig.2 Dynamic model of liquid bundled rocket

图2中的模型主要由助推动力学系统、芯级动力学系统和结构系统3大部分组成，其中助推动力系统共有4个。助推动力学系统和芯级动力学系统分别由燃料路和氧路构成，由上至下分别为贮箱、波纹管、直管、蓄压器、波纹管、泵和推力室。结构系统与各个部件之间相连的虚线表示箭体结构反馈回来的纵向振动速度和纵向振动加速度信号，各个部件之间的实线表示脉动压力和脉动流量。

为验证模型的正确性，利用建立好的各部件模块，搭建了文献[14]中的单路耦合模型，如图3所示。

图3 单组元模型Fig.3 Single component model

图4 固有频率Fig.4 Natural frequency

图5 系统阻尼比Fig.5 System damping ratio

将文献[14]中的数据代入，比较固有频率f和系统阻尼比ξ，如图4，5所示，Reference-1和Reference-2为文献[14]中的固有频率曲线和系统阻尼比曲线，Establishment-1和Establishment-2为图3模型仿真得到的固有频率曲线和系统阻尼比曲线。定量计算结果表明，固有频率与系统阻尼比的偏差在2%以内，可见所建立的各部件模块是正确的。这也说明用各部件模块搭建捆绑火箭模型可行。

3 仿真试验及结果分析

3.1 蓄压器的位置对POGO振动的影响

液体火箭 POGO 振动系统稳定性条件为：任意时刻，若系统阻尼比为正，则POGO振动系统是稳定的；若系统阻尼比为负，则POGO振动系统是不稳定的。通过分析系统阻尼比提升量随时间的变化，得到对POGO振动抑制效果最好的蓄压器位置。

图2中给出可能设置蓄压器的4个位置，分别为助推段氧路(zo)、助推段燃料路(zf)、芯级氧路(xo)、芯级燃料路(xf)，故蓄压器的设置共有16种，如表3所示。

表3中的“■”表示在该位置上设置蓄压器。为确定蓄压器的位置，针对这16种设置，在频域进行仿真，以不设置蓄压器的模型(表3中的种类1)得到的系统阻尼比为标准，得到其他设置种类的系统阻尼比提升量(Δξ)随时间的变化曲线，如图6所示。

表3 蓄压器的安装

图6 系统阻尼比变化量Fig.6 System damping ratio variation

图6中的曲线2～16分别表示表3中序号为2～16的15种蓄压器的设置情况。

由图6(a)可知：曲线2和5系统阻尼比的变化量几乎为0，说明蓄压器只设置在助推段燃料路或芯级燃料路，对POGO振动的抑制效果很差。在曲线2中，虽然在120 s时，系统阻尼比降低，但对比曲线3和曲线4可知：图6(a)中曲线2对系统阻尼比的提升量最高。对比曲线2与3和曲线4与5可知：在助推段和芯级中，蓄压器设置在氧路对POGO振动抑制效果比设置在燃料路时要好。

由图6(b)可知：曲线6，8，9，11的系统阻尼比提升量很小，说明蓄压器在这几种设置下，对POGO振动的抑制效果较差。曲线7和10的系统阻尼比增加量很明显，曲线10的系统阻尼比增加量最大。对比曲线9与10和曲线6与10可知：在助推段和芯级中，蓄压器设置在氧路对POGO振动抑制效果比设置在燃料路时要好。

由曲线3和曲线10可知：曲线10系统阻尼比提升量更大，故蓄压器设置在芯级氧路和助推段氧路时对POGO振动的抑制效果较好。

对比曲线3与7和曲线3与10可知：增加一个蓄压器，系统阻尼比的提升量明显增加。继续增加蓄压器的数量，由图6(c)可知：系统阻尼比的提升量很明显。将曲线16分别与曲线12和15作对比，可发现蓄压器在4个位置上都设置时，系统阻尼比的增加量比在3个位置上设置时要小。这是因为在整个系统中，每增加一个部件，就会使系统阻尼比变得更低，也就会使POGO振动更容易发生。虽然蓄压器可抑制POGO振动效果，但蓄压器过多会降低POGO振动的抑制效果。图6(c)中曲线13和14是因在芯级和助推段的氧路上都没有设置蓄压器，故系统阻尼比的提升量较小，这也说明在助推段和芯级中，蓄压器设置在氧路对POGO振动抑制效果比设置在燃料路时要好。

曲线10和曲线15很相近，系统阻尼比的提升量都很大，但曲线10只设置了2个蓄压器，系统的可靠性更高且运载火箭的质量更轻。由此可知：蓄压器设置在芯级氧路和助推段氧路对POGO振动的抑制效果最好。

3.2 作用力对POGO振动的影响

以蓄压器设置在助推段氧路和芯级氧路作为仿真模型，分析了贮箱、直管、泵、推力室处产生的作用力对系统阻尼比的影响。以考虑全部作用力得到的系统阻尼比为标准，分析了不考虑这几个外力时系统阻尼比的相对变化量(dξ)，如图7所示。

图7 作用力对系统阻尼比的影响Fig.7 Effect of force on system damping ratio

图7中的Pump，Duct，Tank，Thrust，All分别表示不考虑泵处作用力、直管处作用力、贮箱处作用力、推力室处作用力和所有作用力的系统阻尼比相对变化量曲线。

由图7可知：Pump，Duct和Tank这3条曲线虽然在100 s时，系统阻尼比产生了相对较大的波动，但是整体来看系统阻尼比的波动很小。由此可知：泵、直管和贮箱处的作用力对系统阻尼比的影响很小，也就是对POGO振动的影响很小。

对比分析Thrust与All这2条曲线可知：这2条曲线几乎重叠在一起，说明不考虑推力室处产生的作用力时，其他作用力对系统阻尼比几乎没有影响。推力室处产生的作用力对系统阻尼比的影响与所有的作用力对系统阻尼比的影响几乎相当，即推力室处产生的作用力对系统阻尼比的影响在所有的作用力中占据主导地位，对POGO振动的影响很大，贮箱、直管、泵、处产生的作用力对POGO振动几乎没有影响。

由此，可通过只考虑推进剂在推力室处产生的作用力，不考虑其他部件处产生的作用力来简化液体捆绑火箭动力学模型。为进一步验证这一结论，在频域仿真中只考虑推力室处作用力的模型，将得到的系统阻尼比与考虑所有作用力得到的系统阻尼比作比较，结果如图8所示。

图8 系统阻尼比对比结果Fig.8 Contrast result of system damping ratio

图中：V1为考虑了所有外力的系统阻尼比随时间的变化曲线；V2为只考虑推力室处的外力的系统阻尼比随时间的变化曲线。两者之间，系统阻尼比的最大偏差为5.7%。由图8可知：这2条曲线几乎重合，故简化模型可较好地模拟推进系统的特性。这也证明了在推力室处产生的作用力对系统阻尼比的影响在所有的作用力中占据主导地位，对POGO振动的影响最大，贮箱、直管、泵产生的作用力对POGO振动几乎没有影响。

4 结束语

搭建并分析双组元液体捆绑火箭动力学仿真模型，可得以下结论：

1) 在助推段和芯级中，蓄压器设置在氧路对POGO振动的抑制效果比安装在燃料路时要好；

2) 蓄压器设置在芯级氧路和助推段氧路对POGO振动的抑制效果最好；

3) 推力室处产生的作用力对POGO振动的影响在所有的作用力中占据主导地位；

4) 可通过只考虑在推力室处产生的作用力，不考虑其他部件处产生的作用力,简化液体捆绑火箭动力学模型。

后续研究将集中于POGO振动系统的时域仿真，进一步提高POGO振动系统的稳定性。