改进自适应遗传SVM滚动轴承故障诊断

冯 新

(福州大学至诚学院 计算机工程系， 福建 福州 350002)

0 引 言

滚动轴承是轨道工程机械设备的关键组成元件，如果可以在滚动轴承性能衰退的过程中及时检测出故障部位及故障类型，就可以变被动维修到主动维修[1]。一方面提高了滚动轴承的使用寿命，另一方面也大大降低了因故障发现不及时而造成的各种不良后果。所以,对轨道工程机械设备滚动轴承进行故障分类和故障预测具有重大的工程价值。

文中提出一种基于小波变化和改进的自适应遗传算法优化SVM分类的滚动轴承故障诊断模型。首先对采集到的数据进行预处理并做去噪处理，其次利用小波变换对去噪后的信号进行特征提取，继而对提取获得的特征向量做进一步的归一化处理，并使用改进的自适应遗传算法对SVM的相关参数进行优化处理，建立了IAGA-SVM故障诊断模型，最后采用仿真实验来说明笔者所提方法的优越性。

1 模型的描述与建立

1.1 支持向量机原理分析

支持向量机是Vapnik等[2]在统计学理论的结构风险最小化和VC维的基础上提出的一种新的机器学习方法[3]。SVM能够在有限特征信息情况下较好地解决小样本集的回归和分类问题，它比神经网络具有更强的泛化能力[4]。鉴于SVM自身的优越性，现已成为目前最常用、最有效的分类器之一。

假设n个训练样本的样本集表示为:

x∈Rn,y∈{-1,1}

当样本集D为线性可分时，则式(1)为样本的某一超平面方程：

ω·x+b=0(1)

其最优分类超平面必须满足如下方程：

yi(ω·xi+b)≥1(2)

i=1,2,…,n

此时可采用下式对训练样本数据进行分类：

(3)

利用拉格朗日函数来对上述问题进行求解：

(4)

式中：αi----Lagrange乘子,αi≥0,i=1,2,…,n。

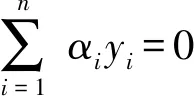
(5)

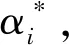
f(x)= sgn(ω*·xi+b*)=

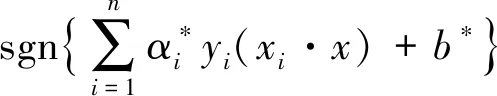
当训练样本为线性不可分时，则需要寻求一个合适的映射函数对数据进行非线性映射。用字母表达为：

φ:Rn→H

x→φ(x)

由Mercer条件可知，若核函数K(xi,xj)可以写成

K(xi,xj)=φ(xi)·φ(xj)

那么问题就转化为在约束条件

αi≥0,i=1,2,…,n

求解二次规划问题：

(7)

求解所得的最优分类函数式为：

(8)

从上述表达式可以看出，核函数的选择对SVM性能的优劣起关键作用。文中选择径向基核函数RBF，即

K(xi,xj)=exp(-γ*‖xi,xj‖2)

γ是描述核函数的作用范围，决定了模型的复杂程度。引入松弛变量ξi≥0，则此时的约束条件由

yi(ωxi+b)≥1

i=1,2,…,n

变为

yi(ω·xi+b)≥1-ξi(9)

i=1,2,…,n

相对应的二次凸规划问题变为

(10)

式中：C----大于零的惩罚因子，用来权衡对错样本的惩罚力度。

SVM分类模型最初被提出来的时候仅仅是用来实现二值分类问题，但实际工程应用中二值分类是非常少有的，往往是多分类问题更加常见。目前使用较多的则为“一对一”、“一对多”和二叉树结构的多分类方法[5]，文中选取基于二叉树结构的支持向量机多分类方法(DT-SVM)。

1.2 自适应遗传算法

自适应遗传算法(Adaptive Genetic Algorithm, AGA)的改进之处是将遗传算法中固定的交叉概率和变异概率进行线性的自适应调整[6]。交叉概率Pc决定了遗传算法的全局搜索能力，变异概率Pm决定了遗传算法的局部搜索能力，所以Pc和Pm对遗传算法的寻优能力起决定性作用。两者的适应度调整公式为：

(11)

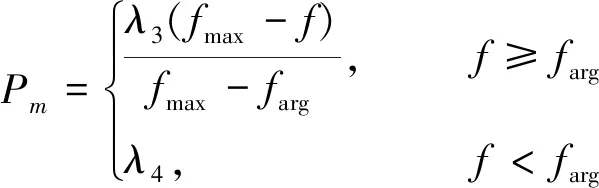
式中：λ1、λ2、λ3、λ4----在[0,1]内随机取值的常数；

fmax----群体中最大的适应度值;

fhigger----参与交叉运算的两个个体中较大的适应度值;

farg----群体的平均适应度值;

f----当前变异个体的适应度值。

由式(11)和式(12)可知，如果fmax=farg，则式(11)和式(12)的分母都变为零，这样的表达在数学中是不成立的。此外fmax=farg表示群体中所有个体的基因组成都是一样的，这时候的优良个体有很大可能是局部最优解而不是全局最优解，从而导致进化无法继续进行下去。

1.3 改进的自适应遗传算法

为了尽可能地避免群体陷入停滞不前的境况，文中对上述自适应遗传算法的公式进行改进：

(13)

式中：Pmax1,Pmin1----分别表示交叉概率的上限和下限;

Pmax2,Pmin2----分别表示变异概率的上限和下限。

这样的设置使得Pc和Pm的适应度值在fmax和farg之间进行非线性的调整，在很大程度上规避了局部收敛的弊端。

2 IAGA-SVM故障诊断模型

文中考虑到支持向量机和遗传算法各自的优缺点，提出一种利用改进的自适应遗传算法优化支持向量机核函数参数和惩罚因子的方法，以此来提高支持向量机的分类能力和泛化能力。采用二进制和实数混合编码的方式对SVM中的相关参数进行遗传编码，以此来提高算法的求解精度，将最终搜索得到的最优结果作为SVM模型的参数进行建模。基于改进的自适应遗传算法优化SVM的故障诊断流程如图1所示。

图1 IAGA-SVM故障诊断模型流程图

3 实验结果与分析

3.1 实验系统的确立

为了证明文中所提IAGA-SVM故障诊断模型的有效性，设计如下实验进行验证。实验数据源自美国凯斯西储大学(Case Western Reserve University)[7]所提供的滚动轴承数据。传感器数据采样频率为12 000 Hz，转速为1 730 r/min，故障损伤直径选用0.053 cm。实验中将滚动轴承故障分为4种状态，分别是正常状态、轴承内圈故障、轴承外圈故障和轴承球体故障[8]。

3.2 IAGA-SVM模型实验结果分析

文中通过小波对信号进行去噪后提取特征向量，再选取各状态下80组样本作为训练样本(共320组)，用于训练模型，选取各状态下20组特征向量为测试样本(共80组)作为测试所用。根据经验设置惩罚系数为[0.005,100],RBF径向基函数的参数为[0.05,100]，最大迭代次数设置为200次。

为了证明文中所提模型的高效性，特设计对比模型来进行实验。遗传算法对支持向量机参数寻优(GA-SVM)、自适应遗传算法对支持向量机参数寻优(AGA-SVM)、改进自适应遗传算法对支持向量机参数寻优(IAGA-SVM)的适应度曲线如图2所示。

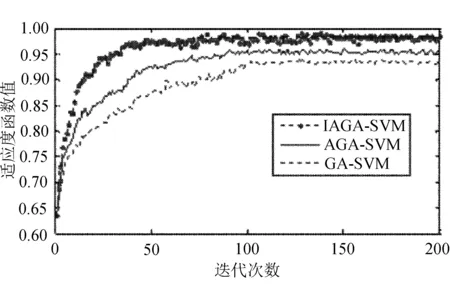
图2 GA-SVM、AGA-SVM和IAGA-SVM的适应度曲线

三种模型的适应度函数均取支持向量机最终的分类准确率。由图2可以看出，GA-SVM于102代左右时适应度变化趋于平稳，但容易造成最终收敛速度慢，甚至存在早熟现象；AGA能够自适应调整交叉率以及变异率，使得其收敛速度加快，因此,可以看到AGA-SVM在63代左右已趋于收敛，相对于GA-SVM而言，它的收敛速度已经加快不少，但AGA算法在种群进化初期容易导致进化停滞不前，陷入局部最优且不利于增强算法的鲁棒性；IAGA-SVM模型仅迭代45次便趋于收敛，明显优于前两种寻优模型，从而使得改进的自适应遗传算法能够更高效的完成收敛，验证了文中所提模型的高效性。

为了测试IAGA-SVM模型对滚动轴承4种状态的辨识度，现对每种故障状态分别选取20个测试样本，使用经过训练之后的IAGA-SVM分类模型对滚动轴承进行测试，测试结果如图3所示。

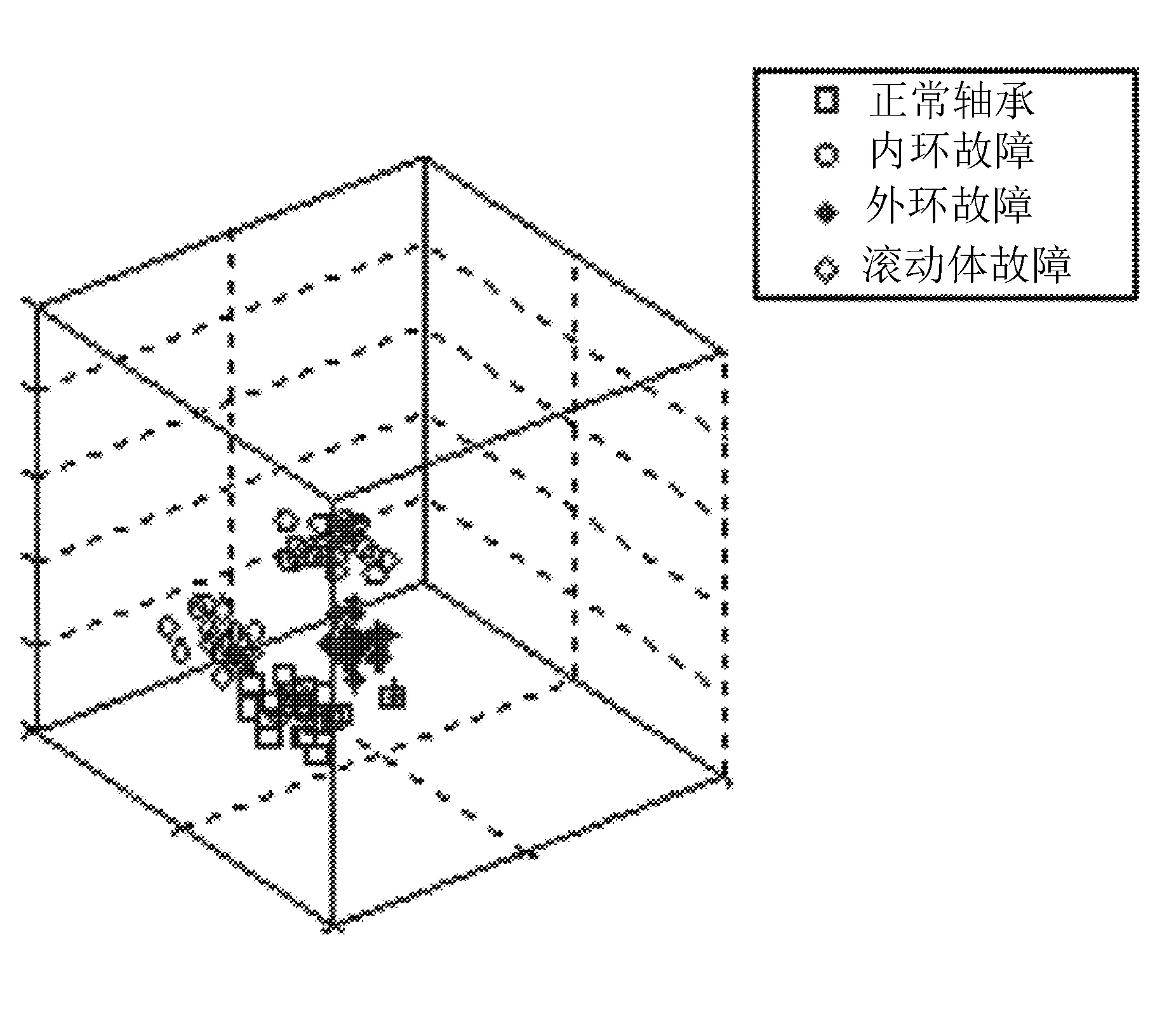
图3 IAGA-SVM模型的分类结果图

由图3可以看出，正常状态、内环故障、外环故障20个测试样本均确诊，其分类准确率分别达到100%，但滚动体故障20个测试样本只有19个测试样本确诊，一个测试样本误诊为正常轴承，分类准确率达到95%。由此可以得到该模型的平均准确率约高达98.75%。可见IAGA-SVM模型作用于滚动轴承故障诊断识别率高，效果明显,具有较大的工程意义。

4 结 语

在对滚动轴承的原始数据进行去噪处理之后，进一步对处理后的信号进行特征提取。针对SVM方法的弊端，特选用自适应遗传算法对SVM的相关参数进行优化处理。但由于自适应遗传算法自身所存在的缺陷，并不能达到预期的分类结果，故而对自适应遗传算法进行改进。

实验结果可以看出,所提出的IAGA-SVM模型对滚动轴承进行故障分类识别，无论在收敛速度上还是在分类的准确率上，优于其他两种实验模型，从而验证了文中所提的故障诊断模型对轴承故障分类的优越性，具有可观的工程价值。