深度指静脉识别技术研究

李 璨， 李 亮， 王 昕

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

0 引 言

生物识别技术[1]就是利用人固有的生理特征(如指纹、脸部、虹膜等)和行为特征(如字迹、声音、步姿等)来进行个人身份的识别鉴定。但事实上这些技术存在还有许多亟待解决的问题，例如在人脸识别方面，当人剃了胡子、戴了眼镜(或口罩)或者是胖了瘦了，这会使得人脸识别结果变得很不稳定[2]。同样,因为指纹是一种外在的生物特征，对于脱皮、有伤痕等低质量指纹存在识别困难。而且有的人指纹特征少、难成像，更重要的是其很容易被仿制[3]，这使得指纹识别多了几分不安全因素。而指静脉是一种内在生物特征，具有唯一性，不会磨损且极难仿制和盗用，具有很高的安全性，且在短时间内生物特征相对稳定[4]。因此指静脉是新一代生物识别技术的典型代表。DBN[5]作为一种典型的深度学习模型近年来被广泛应用，但由于其忽略了图像的二维空间结构信息，难以完全学习图像的局部特征[6]。而LCP[7-8]模型不仅可以提取图像的局部LBP[9]纹理信息，而且可以提取图像邻域像素间的结构信息[10]。

综上所述，文中提出了一种新的基于DBN与LCP相结合的深度指静脉识别算法，该方法利用LCP算法提取指静脉图像的局部纹理特征信息和局部构造信息，从而弥补了DBN模型易忽略图像局部结构信息的不足。同时由于LCP模型对图像的旋转和光照的影响具有较强的鲁棒性，因此,以LCP特征作为DBN网络的输入使得整个深度学习网络更加稳健，与传统的BP[11]分类算法基于SVM[12]和KNN[13]的算法相比较，文中算法能实现对指静脉更加精确的识别。

1 算法原理

1.1 LCP模型

LCP模型所描述的图像特征包含两部分：传统的LBP纹理特征和Microscopic Configuration Operator(MIC) 微观构造特征。两种特征相辅相成,使得LCP模型对图像特征信息的表达十分详尽。LBP模型通过比较某一像素点与其邻域点的像素值的差异来计算LBP特征，表达式如下：

(1)

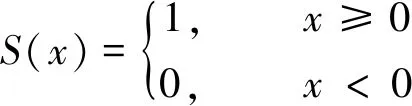
式中:gP----邻域像素点的灰度值;

gC----中心像素的灰度值;

P----邻域点个数;

R----邻域半径。

Mic算子能很好地表达图像的局部微观性质，定义如下：

定义一个P维的矢量

A=(a0,a1,…,aP-1)T

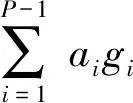
(3)

式中:gc，gi----分别表示中心点像素与邻域点像素;

ai----gi的权重参数。

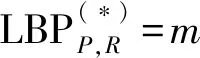
Gm=(gm,0,gm,1,…,gm,Om-1)T

如果用Vi,0,Vi,1,…,Vi,P-1(i=0,1,…,Om-1)表示以第i个具有m模式的像素为中心的邻域点像素的灰度值，则图像中所有模式近邻像素的灰度值构成矩阵Vm：

(4)

若用Am=(am0,am1,…,amP-1)T表示模式的参数矢量，则最优参数矢量应该满足：

Gm=VmAm(5)

因式(5)是超定方程，采用最小二乘法可求其唯一解：

(6)

同时为了克服图像旋转引起Am的周期变化，引入傅里叶变换。用Fm表示Am的P点一维傅里叶变换。

(7)

式中:Fm(k)----Fm的第i个元素;

Am(i)----Am的第i个元素，且Fm具有旋转不变性，取其幅度作为图像的局部微观构造Mic特征，则Mic定义如下：

|Fm|=[|Fm(0)||Fm(1)|…|Fm(P-1)|]T(8)

最终将LBP特征与Mic特征进行融合用于表示LCP特征：

LCP={[|F0|;O0];[|F1|;O1];…;[|FM-1|;OM-1]}(9)

式中: |Fi|----由式(8)计算而来;

Oi----第i个相应LBP模式出现的次数;

M----LBP模式数量。

1.2 DBN模型

DBN[7]深度信念网络是由Hinton与其学生在2006年提出的,其由一系列无监督受限玻尔兹曼机(Restricted Boltzmann Machines,RBMS)[14]和输出层的前馈反向传播(Feed Forward Back Propagation,BP)[15]神经网络构成。它本质上就是一个包含多个隐藏层的概率模型。整体结构如图1所示。

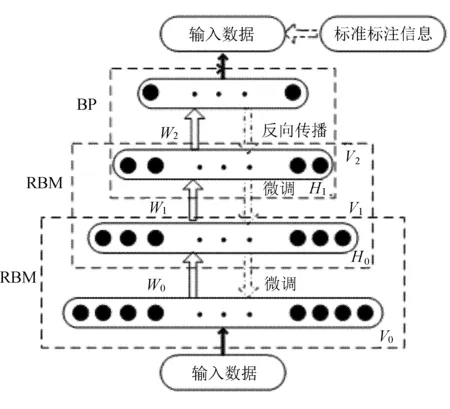
图1 DBN模型结构图

这一系列的RBMS通过层叠的关系将前一层RBM的输出作为后一层RBM的输入,从而构成了深度RBMS网络。在DBN网络的最后一层采用有监督的BP神经网络实现对整体网络的参数进行调整与分类。并且通常把一系列RBMS的无监督训练称之为预训练，而把深层RBMS训练得到的网络参数作为整体网络参数赋给BP的阶段称为微调。对于一个具有l层隐藏层的DBN来说，可视单元与隐藏单元之间的联合分布可表示为：

P(v,h(1),h(2),…,h(l))=P(v|h(1))p(h(2)|h(1))…

P(h(l-1)|h(l))(10)

式中：v----DBN的可视单元,v=h(0)；

h(k)----第k层隐藏单元,k=1,2,…,l。

第k层与第k+1层的隐藏单元满足：

(11)

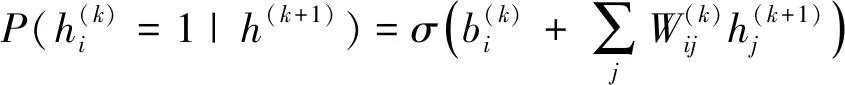
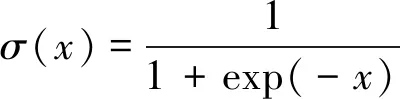
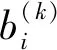
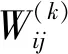
σ(x)----激活函数，在DBN网络中将P(h(l-1),h(l))称为一个RBM模型。

2 基于LCP和DBN的深度指静脉识别

网络训练的好坏决定了对LCP特征学习的准确度。DBN的训练过程如下：

首先,以全局的LCP特征作为输入，对第一层RBM进行无监督训练，得到第一层的最优参数。

然后，以第一层RBM的输出数据作为第二层的输入进行无监督训练得到第二层RBM的参数值。以此类推，逐层训练得到每一层的参数值。

最后，通过全局训练对各层参数进行微调，从而实现DBN收敛并达到全局最优，并进行回归分类。该训练过程规避了目标过拟合的现象。

此时深度DBN网络的联合分布表示如下：

P(H,h(1),h(2),…,h(l))=P(H|h(1))p(h(2)|h(1))…

P(h(l-1)|h(l))(14)

式中:H----LCP特征;

h(1),h(2),…,h(l)----DBN网络对H特征学习到不同层次下的高级特征,其影响到DBN网络学习的有效性。

因此LCP的纹理特征部分我们选择统一模式的LBP，这样做有两大好处：

4.3 硫酸盐含量在17.66%～26.39%范围内和溶液酸碱度存在线性关系，控制溶液的pH值可以控制硫酸盐的含量。但考虑到此次样本量比较小，样品的含量及pH比较集中，未涉及药典规定的边缘pH值，后期将进行更加严密的实验及论证，对拟合方程进行进一步的确认和优化，以求在符合质量标准要求、确保准确度的前提下，简化检验操作的流程步骤。

1)非统一模式LBP具有2p种模式。而统一LBP只有(p(p-1)+3)种模式，即特征维数大大降低。而且虽然模式减少了很多，但其仍然包含了90%以上的LBP模式信息。

2)统一LBP对灰度平移变换具有不变性，且能更好描述局部纹理特征。

文中的整体实现步骤如下：

1)对指静脉图像进行尺度归一化处理为128*128,然后对图像进行4*4分块；

2)提取各子块的LCP特征；

3)将各子块的LCP特征连接成全局的LCP特征；

4)对特征向量进行归一化处理并输入到DBN网络；

5)对DBN网络进行逐层训练以获得最优网络参数；

6)利用BP神经网络进行全局微调；

7)在网络顶层进行回归分类并计算识别率。

3 实验过程与结果

实验图像数据库包含64个手指共960幅图像，每个手指有15幅图像。所有图像均已作了尺度归一化处理。

经过归一化处理后的部分指静脉图像如图2所示。

实验中随机取每个手指的10幅图像作为训练样本,余下的5幅图像作为测试样本。实验平台是Windows10专业版PC机处理器为intel(R)core(TM)i5-3470cpu@3.20 GHz,内存是4 GB，软件版本MATLAB2013a(64位)。

3.1 DBN中各参数的确定

DBN网络构建完成后需要设定模型的最佳参数，经过反复验证，文中实验DBN的层数设置为4，学习率设置为0.001，每层迭代次数为30次。

隐含层节点数的学习曲线如图3所示。

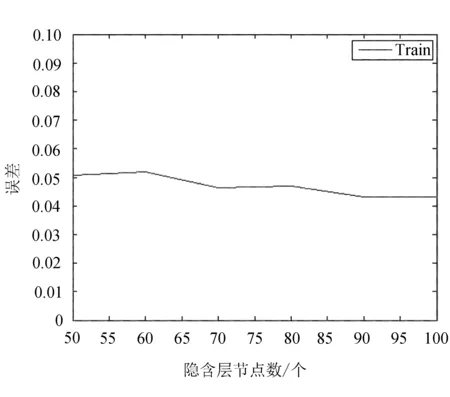
图3 隐含层节点数的学习曲线

从图3可以看出，当隐藏层节点数大于90以后， DBN的训练集误差趋于稳定。因此,各层隐含节点的个数设置为100，为了进一步确定整个DBN网络的结构，进行了RBM深度测试实验，实验结果见表1。

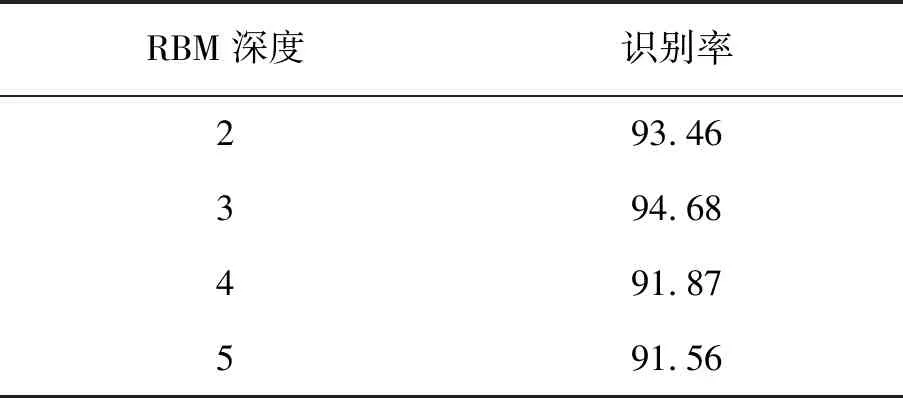
表1 不同RBM深度对识别率的影响 %

由表1的实验结果可以看出,当DBN网络的RBM深度为3时,识别率达到最大94.68%。

所以本实验构建的DBN结构为m-100-100-100-64。其中，m表示输入DBN的LCP特征向量的维数。文中取P=8,R=1，所以最终m=2 240。

3.2 对比实验

为了验证文中提出的深度指静脉识别算法的有效性，设置了两组对比实验。分别选取有监督的BP神经网络和SVM及KNN(K值取3)三种分类算法作为对比。实验中各组均采用相同的测试集和训练集，所用特征向量均为LCP特征。实验结果见表2。

表2 不同分类算法识别率对比 %

由表2的实验结果可以看出，DBN 网络明显优于传统有监督的分类学习模型，这是因为DBN作为一种深度学习模型，能够通过多层非线性结构对输入数据自主地提取具有分类能力的特征再分类学习，从而提高了对指静脉的识别。这正是浅层BP网络、KNN分类算法及SVM所不具备的。而且，随着图像库中指静脉图像数目的增加，文中算法的识别率将更高。

4 结 语

经过多年研究努力，指静脉识别的研究获得了很大进展，在门禁、考勤、图书馆、银行、监狱、汽车安全等领域得到了一定的应用。文中所提出的深度指静脉识别方法相较于传统的有监督分类算法有着明显的优势，LCP特征与DBN网络相结合使得该模型能通过多层非线性结构对输入数据进行自主的再分类学习，从而对指静脉的识别率更高。将文中算法与传统的BP分类算法、SVM分类算法及KNN分类算法进行了对比实验，证明文中算法的优越性。