遗传算法下的粗糙集属性约简算法及其有效性分析

郑文彬 , 胡敏杰*， 何秋红

(1.闽南师范大学 计算机学院, 福建 漳州 363000;2.闽南师范大学 福建省粒计算及其应用重点实验室， 福建 漳州 363000)

0 引 言

粗糙集理论属于数据挖掘方法中的高效方法，也是全新强有力对不确定性信息数学工具处理的方法。不确定性信息处理指的是对于不完整、模糊及不精准信息和组合信息实现处理，其被广泛应用到机器学习、人工智能、故障诊断、模式识别及数据分析挖掘中。使用粗糙集约简，能够选择条件属性集，将条件属性和决策不相关删除，使用条件属性约简集替代原本属性集。对数据量较大、属性维度较高的信息系统，在人们可接受时间及具有有效资源背景下，根据遍历及枚举的方法无法得到最小属性约简，人们一般只能够得到属性近似约简，粗糙集属性约简算法为目前高效方法，所以使属性约简算法效率提高，对粗糙集属性约简来说尤为重要。

1 粗糙集的基本理论

粗糙集理论指的是对不确定性处理的数学工具，也是全新软计算方法。目前，粗糙集备受人们的重视，其有效性已经被证实，属于现代国际中人工智能理论和应用领域中的研究热点。在多种实际系统中都具有不同程度的不确定性因素，收集数据常常具有不完整、不确定及噪声，所以需要对其进行处理。粗糙集理论使知识理解划分成为数据，每个被划分的集合就是概念。粗糙集理论思想就是使用已知知识库，使不确定及不精准知识使用已知知识库刻画，此理论和其他处理不精准及不确定问题理论的主要区别就是其不需要提供问题需要的数据集合之外信息，所以在处理问题不确定描述过程中较为客观，因为此理论没有处理不确定及不精准原始数据的机制，那么此理论及概率论等处理具有一定的互补性[1]。粗糙集理论的主要定义为：

1)决策表。决策表S指的是四元组S≤U,R,V,F>，其中的U指的是非空有限对象集，称之为论域;R=C∪D的属性集合，C指的是条件属性集，D指的是结果属性集，V指的是属性值集合。F指的是信息函数，属于U中每个对象x的属性值。

2)不可分辨关系。在决策表S中，对每个属性自己定义成为不可分辨关系，也就是：

IND(B)= {(x,y)∣(x,y)∈U2,

∀b∈B(b(x)=b(y))}

3)正域。假设U属于论域，P与Q指的是U中的两个等价关系簇。

4)下近似集。对于每个概念中的X与不可分辨关系，包括在X中的最大可定义集都是以B进行确定的[2]。

2 遗传算法分析

遗传算法是将达尔文所提出的生物进化论和孟德尔提出的遗传学理论，对自然界生物从低级到高级进行模拟的高级净化过程，将初始种群作为起点，使用适者生存自然法则对个体进行选择，并且使用变异、交叉等策略产生下一代种群，逐渐进化到满足期望条件。遗传算法将净化思想作为基础，常用来对复杂优化问题进行解决。在遗传算法不断完善及发展的过程中，算法效率在不断的提高。并且遗传算法自身具备开放性，能够使其和其他算法相互融合，以此提高算法的效率[3]。

2.1 种群和个体

种群为遗传算法中求解问题解空间子集，种群中全部元素都属于个体，其在迭代过程中在不断的发生变化，但是种群个体数量不会发生变化。

2.2 编码

编码指的是将需要优化的问题朝着遗传算法容易处理的方式进行转变，遗传算法性能和编码方式具有一定的联系，所以选择合适求解问题编码方式是算法设计的主要内容，常见编码方式包括树型编码、二进制编码、自适应编码及实数编码。

2.3 选择

选择指的是以个体适应度值的优劣程度对种群个体进行选择，也就是以一定概率Pr从上一代种群中实现个体选择，之后进行操作。一般选择方法包括随机便利、轮盘赌和排序选择等。遗传算法中最早的选择策略就是轮盘赌，此方法使种群中全部个体适应度的和作为轮盘，每个个体和轮盘中的某个区域进行对应，个体适应度越高，那么占比就会越高[4]。

2.4 适应度函数

适应度指的是种群个体对于环境适应程度，此指标主要是对种群中个体优劣程度进行描述。适应度函数主要指的是个体在进化计算过程中的最优解程度，遗传算法在搜索过程中不利用外部信息评价，以此导致适应度成为种群个体评价的主要标准，所以选择适应度函数和设计对遗传算法具有一定的影响。

2.5 交叉

交叉操作指的是以一定概率Pc从种群种选择种群个体构成配对，之后将其基因串某部分实现交叉，以此产生全新种群个体过程。交叉操作不仅保持原本种群优良个体特点，并且还使算法能够对全新基因空间进行搜索，使全新种群个体具备多样性。二进制编码大部分都是利用单点交叉策略。

假设每个个体都具有八位二进制表达，其中的两个个体分别为F1=11100111，F2=10011010，假如交叉位置为3，那么个体低三位交换，得到全新个体：R1=11100010，R2=10011111。在进行个体交叉操作的过程中，对每次个体交叉操作概率进行控制[5]。

3 基于遗传算法的粗糙集属性约简算法

3.1 遗传约简算法

在决策问题的过程中，寻找最小相对约简具有重要的作用，结合遗传算法和粗糙集，效果良好。

3.1.1 编码方式

因为遗传算法无法对空间解数据进行直接处理，所以利用编码使其转变成为遗传空间基因型串结构数据。利用固定长度二进制符号对群体个体进行表示，等位基因通过二值符号集{0,1}构成。初始群体个体基因使用均匀发布随机数表示，比如100111001000011100就为个体，此个体染色体长度为n=18，其中的每位都与条件属性相互对应。如果取值为1,那么其指的是选择某个对应条件属性，如果取值为0，那么就表示不对相应条件属性进行表示[6]。

3.1.2 个体适应度评价

将适应度函数定义成为：

式中： card(x)----染色体中1的数量，也就是染色体中条件属性的数量;

n----染色体长度，也就是条件属性数量;

k----决策属性对于染色体条件属性的依赖度。此函数能够对染色体控制最小约简方向：k越大，表示决策属性D对于属性C依赖程度就会越强;在k为1的时候，决策信息通过条件信息进行确定。

利用card对染色体中条件属性长度进行控制，以此所创建的适应度函数不仅能够保证决策属性对于整体条件属性依赖度不改变，还能够寻找具有条件属性小的约简。

3.1.3 选择操作

利用适应度比例选择方法，从目前群体中选择优良个体，将其到下一代群体中进行复制。具体流程为：

1)对群体中全部个体适应度总和进行计算；

2)对个体相对适应度大小进行计算，也就是个体到下一代群体遗传的概率；

3)利用赌盘操作模拟对个体被选中数量进行确定[7]。

3.1.4 交叉操作

使用单点交叉算子进行执行。对群体个体实现两两随机配对，对每对相互配对个体随机实现交叉点的设置，对每对配对个体根据假设的交叉概率Pc在交叉点中相互交换个体部分染色体，以此产生全新个体。

3.1.5 变异操作

利用变异算法使个体基因根据编译概率指定变异点，使每个指定变异点中的属性不变异，对其基因值进行取反运算，以此产生全新个体。

3.1.6 最优保存

在得到全新个体以后，假如最坏个体适应值比上一代最好个体适应值要小，那么上一代最好个体替代最新最坏个体，此方法能够保证算法收敛。

3.2 基于遗传算法粗糙集属性约简算法

因为遗传算法无法实现理解空间解数据直接处理，所以就要利用编码使其转变成为遗传空间中基因型串结构数据。文中利用固定长度二进制符号串表示群体个体，等位基因通过二值符号集构成。初始群体中的个体基因值使用均值分布随机数生成，比如1001100就是个体，其中的每位对应条件属性。如果值为1，那么对相应条件属性选择；假如值为0，那么表示不对相应条件属性选择，以上个体相应属性为{c1，c4，c5}[8]。

3.2.1 基于区分矩阵粗糙集约简算法

因为二进制区分矩阵核和基于正区域核两者定义不同，其不仅能够在决策表中使用，也能够应用到不相容决策表中。

对给定信息系统S=(U,A,V,F)定义成为区分矩阵M={Mij}，其中Mij表示为：

式中：d(xi)----U中全部和xi在关系中的等价元素相应决策属性值创建的集合基数。

在简化分区矩阵中使关系IND(C)值得出，求解方法复杂度为0(m*n*logn)，其中m指的是属性集数量，n指的是U元素数量，但是并不理想。算法为：

1)输入决策表S-(U,C,D,V,F,d),U={x1,x2,…,xn},C={c1,c2,…,cr}。

2)实现IND(C)的输出。

3)对每个ci(i=1，2，…，r)得到f(xj)(j=1,2，…，n)的最小值和最大值，最大值为Mi，最小值为mi。

4)通过静态链表对对象进行存储，分别为x1，x2,…，xn，使表头指针为x1。

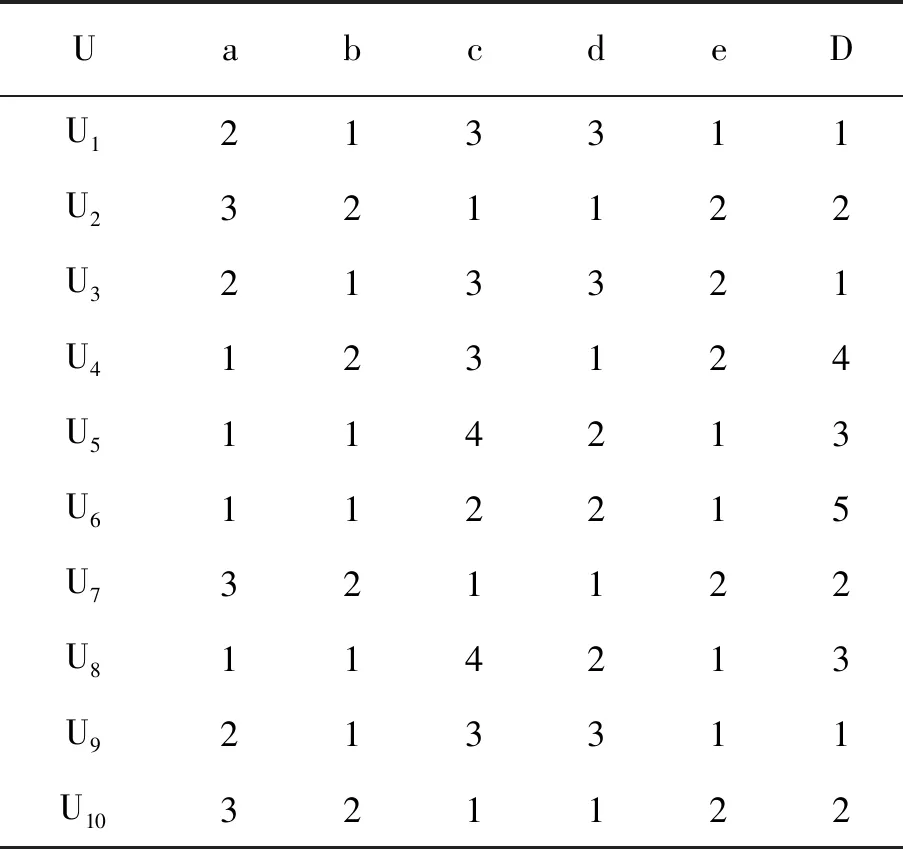
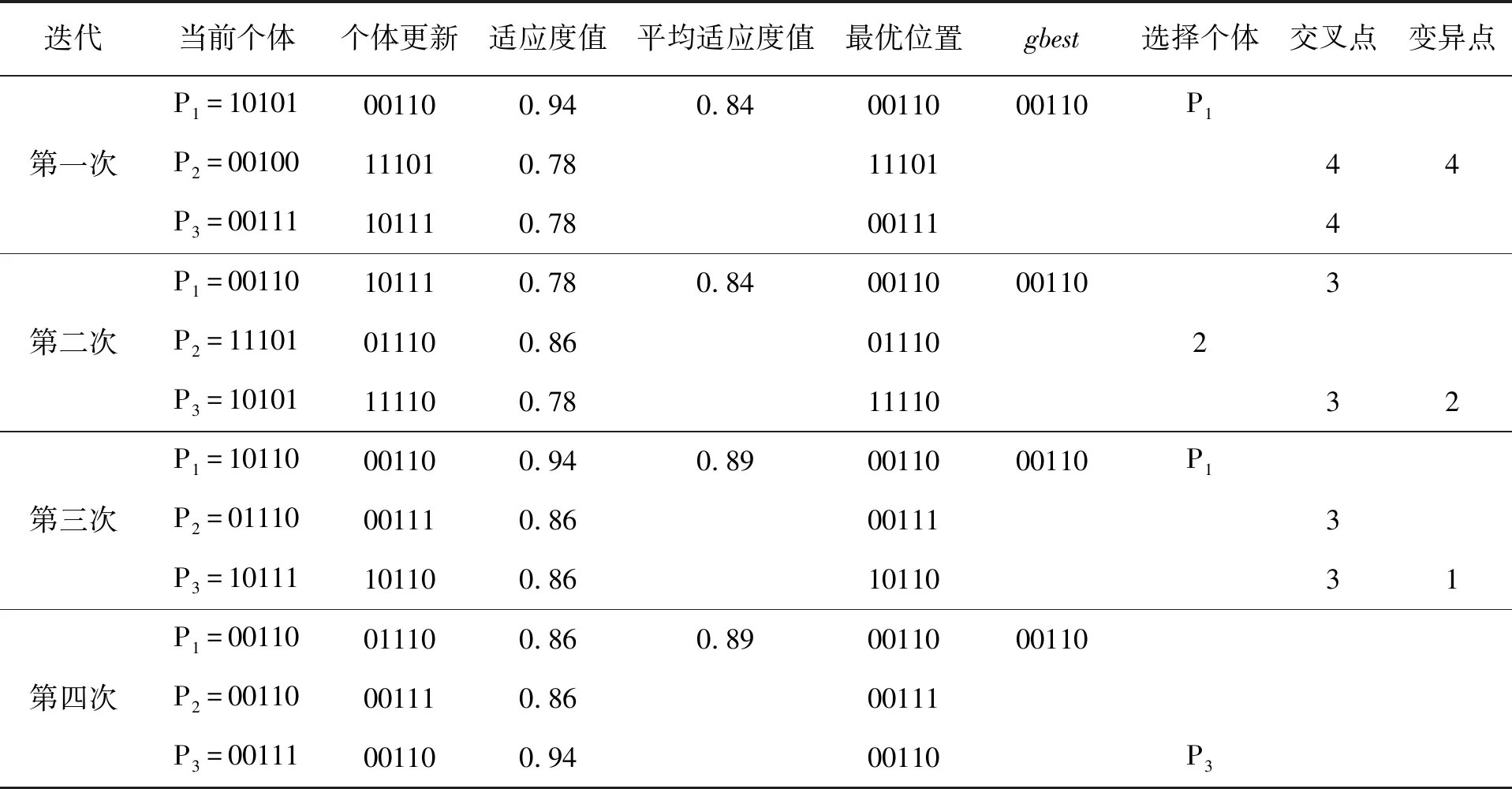
5)For(i=1；i

7)如果Bi中的全部对象在决策属性中的值相同，那么使Bi中的第一个对象融入到U中。

文中是遗传算法和粗糙集结合实现约简，免疫遗传算法能够结合生物免疫系统自适应识别及排除侵入机体抗原性异物功能，在遗传算法中融入生物免疫系统记忆、学习、识别及多样性的特点，免疫遗传约简算法的思路为：

1)主要步骤就是选择适应度函数，之后创建适应度函数，表示为：

式中:r----染色体中的解；

n----染色体长度；

card(M)----M区分矩阵中的非空元素数量，满足M。

适应度函数前部分中的驱使算法朝着属性数最小方向进行搜索，后部分保证R为约简[9]。

2)促进产生抗体。要想能够促进抗体高适应度，就要抑制高浓度抗体。抗体相似性利用抗体编码欧几里得距离进行表示，两个抗体之间的欧几里得距离表示为：

式中，d值在不断的增加，那么两者相似度就会越低。假如d为0，那么表示抗体一致。

3)选择操作。使群体抗体利用轮盘赌选择方式从目前抗体群中将优良个体进行选择，将其到下一代群体中进行复制。利用相似性矢量矩作为选择概率，将其定义为：

式中:α、β----常数调节因子;

F(x)----适应度函数。

通过以上公式可以看出，此选择概率不仅和抗体适应度具有密切的关系，还和抗体相似度具有密切的关系。此种抗体群体的选择能够避免出现抗体陷入局部最优解问题，使抗体多样性进行保证。

4)在算法中使用基本位变异算子及单点交叉算法，利用最优保存策略对算法收敛进行保证。

①使用基数排序算法对矩阵进行简化区分，假如决策属性D和条件属性C依赖度和属性核进行确定，两者相等，那么结束运算;如果不相等，进行以下操作。

②通过随机产生m个长度n二进制串代表个体构成初始抗体群，对核中的属性相应值为1，否则值为0，对初始抗体群中的个体适应度进行计算。

③以上一步所计算的适应度，刺激适应度比较大的个体，对抗体浓度进行计算，删除大浓度个体。

④对选择个体概率进行计算，利用轮盘赌方法对个体进行选择。

⑤根据交叉及变异概率产生全新个体，变异的时候保证核属性相应基因位不出现变异。

⑥使用最优保存策略取出父代个体中高适应度个体，将其到下一代个体中进行复制。

⑦如果使用十代最优个体适应度不提高，那么计算终止。如果提高，转到③继续计算。

文中使用的算法在对等价关系进行计算的过程中使用基数排序思想，使等价关系计算时间复杂度表示为O(m*n)，空间复杂度表示为O(n)。在运算算法的过程中融合决策属性对于条件属性依赖度，并且和抗体浓度相互结合，对净化过程个体多样性进行维持，使搜索能力得到提高，避免出现局部最优。

3.2.2 算法可行性分析

文中所提出的基于遗传算法的粗糙集属性约简算法设计过程中，使用Sigmoid函数使连续优化问题算法和粗糙属性约简问题相互联系，以此对文中算法可操作性进行验证。之后所分析的最优更新操作都能够提高文中算法约简效果，并且使用适应度函数能够对种群中接近约简、属性数较少粒子保存进行保证，所以通过多次迭代之后还能够寻找最小约简，以对文中算法有效性进行保证[10]。

4 算法实验

为了对文中算法有效性及可行性进行分析，列举简单实例对算法运算步骤进行说明，之后利用大数据约简对算法有效性进行验证。

其中的实例对象集合为U={U1，U2,…,U10}，条件属性集表示为C={a，b，c，d，e}，决策属性表示为{D}。

利用可辨识矩阵方法对属性约简结果进行该计算，将其作为对比信息，以下为属性约简步骤。假如粒子维数表示为5，种群数目表示为3，最大迭代次数表示为T=10。

首先，以属性集C={a，b，c，d，e}对属性依赖度值进行计算；之后，通过初始化粒子群和属性，将其使用二进制方式进行表示：P1=10101，P2=00100，P3=00111。以粒子适应度值计算，设置全局最优粒子为P1=10101。

决策信息系统实例见表1。

表1 决策信息系统实例

最后，实现遗传算法循环迭代，因为迭代计算过程复杂，计算步骤结果描述见表2。

表2 计算步骤结果的描述

因为全局最优粒子gbest连续四次迭代都没有出现变化，所以运算终止，全局最优位置为00110，也就是此决策表中的最小相对约简属性表示为cd。文中所设计的算法和相关研究学者算法对比表明，此算法能够有效节约运算时间。

5 结 语

粗糙集理论属于全新处理不确定性、含糊性问题的数学工具，其主要优势就是不需要相关数据预备及其他信息，所以粗糙集理论因为自身的优势备受人们重视，其和遗传算法相互结合成为研究的重点内容。属性约简为粗糙集理论中的主要研究内容，但是寻找决策表最小约简为较难的问题。文中所提出的基于遗传算法粗糙集约简方法，不仅能够提高算法的局部搜索能力，还能够保证此算法全局寻优特点。实验结果表明，此算法不仅能够实现决策表约简，在对大规模数据计算的时候节约时间。在今后工作过程中，要对遗传约简算法继续进行完善。