一种宽范围的移相电路
林志琦, 邵建波, 李严军
(长春工业大学 电气与电子工程学院, 吉林 长春 130012)
0 引 言
移相器是一种对相位变化进行控制的元件,广泛应用于雷达、导弹控制、加速器以及通信等各个领域[1]。 同时,相同频率的两个信号之间的相移是模拟和分析电子工业中继电保护领域事故的重要手段[2]。比如在相控天线中,需要使用移相器对天线阵列各单元信号的相位进行控制,以形成空间波束并控制其进行扫描[3]。
移相器从元器件组成上主要包括数字移相器和模拟移相器[4]。虽然数字移相器近年来发展比较热门且有诸多优点,但相比于数字移相器,模拟移相器具有连续调相、 结构简单、 复杂度低等优点,仍具有一定的实际意义。
从原理上说,数字移相器的精度是有限的,而模拟移相器在这方面是连续的,且精度高。
文中将从两种最简单的一阶RC电路进行介绍与分析,并根据其特性设计出一种连续可调的0~π等幅的移相电路。
1 一阶RC的电路分析与对比
1.1 一阶RC移相电路组成
一阶RC电路在关于移相方面可分为RC超前电路与RC滞后电路。其电路结构可以仅有一个电阻和电容组成。
一阶RC超前、滞后电路连接上的对比如图1所示。
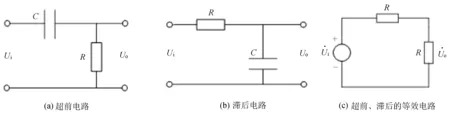
图1 一阶RC超前、滞后电路连接上的对比
其工作原理如下:
1)RC超前电路见图1(a),从电容器的两端电压落后于电流90°出发[5]。电路从输入中顺时针看,电容器C接在电阻器R的前面,电容器C中的电流相位超前于电压相位,根据串联电路的特点,电容器C中的电流正是电阻器R中的电流,这个电流在电阻器R上的电压降就是输出电压,所以输出电压超前[6]。
2)如图1(b)中由于电容器C与输出并联,根据并联电路电压相等的原理,输出电压就是电容器两端的电压[7]。因电容器两端的电压滞后于电流,所以输出电压滞后。
从图1(a)和(b)中可以发现,电路连接仅使用电阻器和电容器来形成分压电路,因此,它们等效于图1(c)所示电路。
1.2 一阶RC电路的数学分析及相位特性
在分析对比了两种电路的工作原理后,进一步通过数学分析的方法得出精确的相位与幅度及频率的关系。
根据图1(c)和分压的原理对于图1(b)有:
(1)
其中输出电压有效值为:
(2)
输出电压相位为:
φ2=∠-arctan(ωRC)(3)
从式(1)可以看出,当信号的频率一定时,输出电压的有效值与相位都随电路的时间常数变化而变化。设电容器C的容量为一定值,如果电阻值R从0到∞变化,则相位从π/2~0 变化。
同理,对于图1(a)有:
(4)
其中输出电压有效值为:
(5)
输出电压相位为:
(6)
由式(4)可知,在与上面相同的条件下,则有当输入信号的角频率一定时,输出电压的大小及相位随电路参数的变化而改变。设电容C的容量值不变,如果电阻值R从0到∞变化,则相位从0~-π/2变化。
根据式(2)、式(3)、式(5)和式(6)绘出一阶RC超前电路和一阶RC滞后电路,电路的输出幅度随着移相角度的变化如图2所示。
在图2中对频率、时间常数值及幅度值进行了归一化处理。
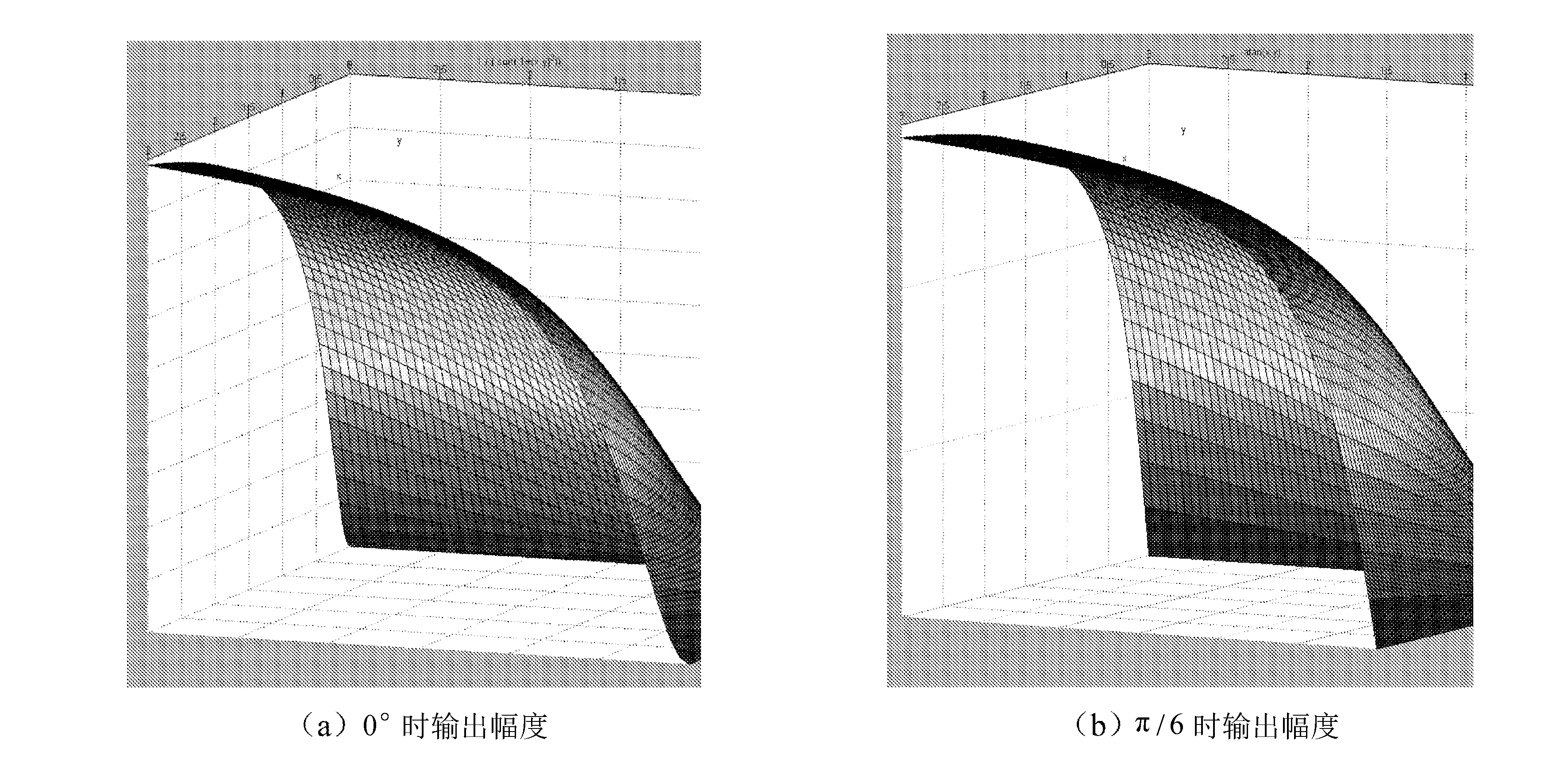
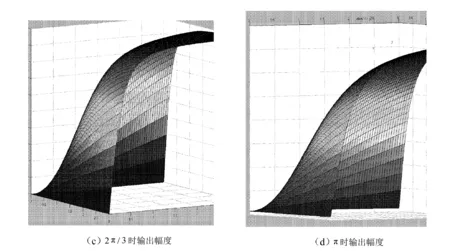
图2 一阶RC超前电路和一阶RC滞后电路的输出幅度随着移相角度的变化
由图2可以看出,对于超前电路,当信号的周期远大于电路的时间常数时,电路的移相为0°,输入输出幅度相等。这时该电路已经变为耦合电路。对于滞后移相电路,当信号周期比时间常数小很多时,电路的移相为0°,输入输出幅度相等,此时该电路变为低通滤波电路。
通常情况下,移相大小与时间常数有关,与频率有关,输出信号幅度也与相位和频率有关。
2 高精度的0~π模拟移相电路与数字移相器的对比
2.1 高精度的0~π模拟移相原理设计
从图2可以看出,图1(a)与(b)两种电路的的移相角度不同时输出幅度也不同,而在实际应用中,通常要求移相器电路的输出幅度与移相角度及工作频率无关。为了实现输出幅度与移相角度无关,仔细观察图2(a)与(b),图2(c)与(d)会发现这两对曲面的变化正好相反,可以利用这种特性进行补偿,实现输出幅度与移相角度和信号频率无关。
输出幅度与移相角度无关的电路如图3所示。
该电路可在0~π之间移相,并保持输入与输出信号幅度相等。
图3中,输入信号Ui同时加到由C1、R1构成的超前移相电路和由R2、C2构成的滞后移相电路上,Uce是超前移相电路的输出,Ude是滞后移相电路的输出,两者的差为总输出:
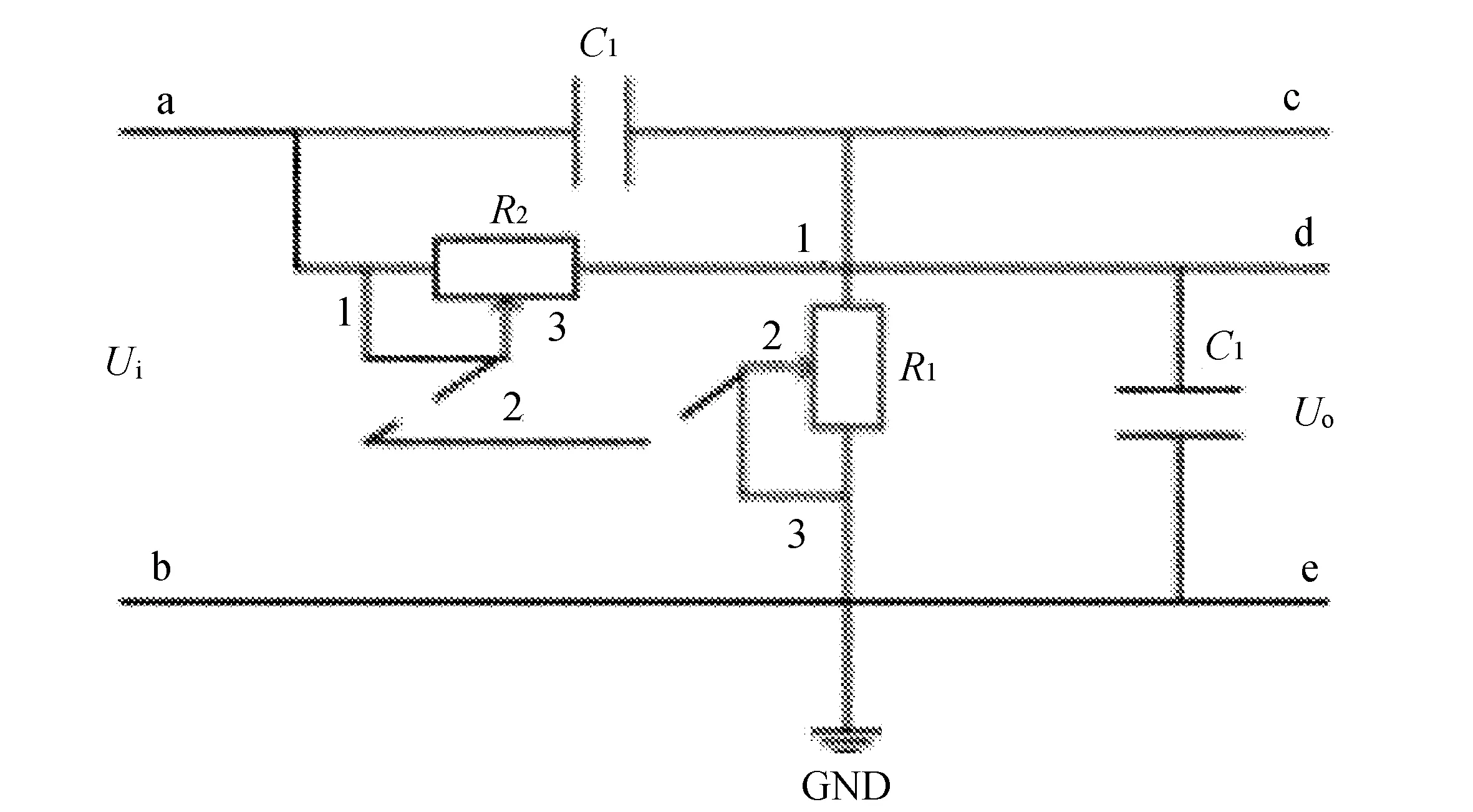
图3 一阶RC超前电路和一阶RC滞后电路共同组成的0~ π电路
当C1=C2=C;R1=R2=R时
(7)
其中输出电压有效值为:
(8)
输出电压相位为:
φ2=∠-2arctanωRC(9)
式(8)说明这种移相电路的输出电压与输入电压幅度相等,保证了幅值不随频率及相位的变化而变化。输出电压的相位可通过改变电路的时间常数来调节。
设电容器C的容量值一定时,如果电阻器R的阻值从0到∞变化,则相位从0~-π变化;当R=0时,则φ2=0°,输出电压Uo与输入电压Ui同相位。当R=∞时,则φ2=π,输出电压Uo与输入电压Ui相反。当0 关于模拟移相器的性能及精度问题,可以依据以下推导公式进行计算。 由式(9)可知,输出电压相位φ2是关于R和C的函数。即可用φ2=f(R,C)表示。根据式(9)可得出φ2分别对R,C偏导公式如下: (10) 从式(10)、式(11)中可以知道,相位的变化与R、C成一定的关系。而在实际应用中,通常是以电容C为不变量,而电阻R是连续可变的。 当ωCR≫1时,则式(10)可写成: (12) 根据实际电路可以假设ω=300 Hz,C=1 μF,R=10 kΩ,根据式(12),当∂R=0.1 Ω时,|∂φ2|=1/1 500。由此可以看出,该模拟移相器的精度已高达6.67°×10-5,这远比6位数字式移相器的精度要高。 文中提到数字式移相器精度有限,这是因为数字式移相器的精度主要是靠A/D,D/A转换器的位数决定的。而这里的位数是指能够将模拟信号与N位二进制数字信号相互转换的。比如说一个6位的A/D转换器,它能够将模拟输入信号转换成6位二进制数字输出信号,即将连续的模拟信号分成了26份,并将其数字化,显然这是存在一定误差的。而且随着要求的精度越高,对数字式的移相器中A/D,D/A的位数要求就越高,以现有的技术会提高成本而且不易实现[8]。因此,在考虑成本时,数字移相器应用到精度要求不是很高的场合是相对合理的,而模拟移相器就很好地解决了这些问题。因为模拟移相器本身就是处理模拟信号的,没有对输入信号进行数字化,精度高,而且是连续可调的,根据现有的半导体技术将电阻制作成更高精度的比制作相应精度的A/D,D/A转换器容易得多,成本更低[9]。 在实际应用中,模拟移相器与数字式移相器相比结构简单实用,且易于实现。 图3中,电路的输出是两个信号的差值,将差动信号由运算放大器转为单端信号,0~π移相电路原理如图4所示。 图4 0~π移相电路原理 实验表明,图4中电路的参数可以在300~4 000 Hz范围内,实现0~ π的移相。 实验电路的实物图如图5所示。 图5 实验电路的实物图 测试结果如图6所示。 图6 实际测量的移相效果波形 该电路很好地实现了0~ π的等幅移相。 该实验电路可以应用到一些领域,比如锁相放大器、调幅广播等。就调幅广播而言, 它具有频带窄、容纳多个无线电台、传输距离远等优点[10]。但是也存在一些问题,如混合站和串扰等,而传统的二极管检测电路也存在这些问题。同步检测是基于幅度调制的双边带。它选择接收较少的干扰或干扰自由边带,以减少甚至消除干扰。同步检测的优点还在于其音质比调频广播稍差,而同步检测电路的核心部件就可以使用该移相器电路。 经过上述理论推导及实验测试结果充分说明了本设计的合理性及可行性,并且本实验是使用简单的分立元件就很好地实现了高精度0~ π等幅移相,结构简单易于实现、成本低廉、应用广泛。由于篇幅有限,文中没有对一些客观条件进行讨论。比如R、C等元件的老化,温度对电路的影响等。这些问题的解决,会进一步提高该电路的稳定性及精度,后续会继续研究并解决这些问题。2.2 性能分析及模拟与数字移相电路的比较

3 移相器的实现与测试
3.1 实用的0~ π等幅移相器的实现


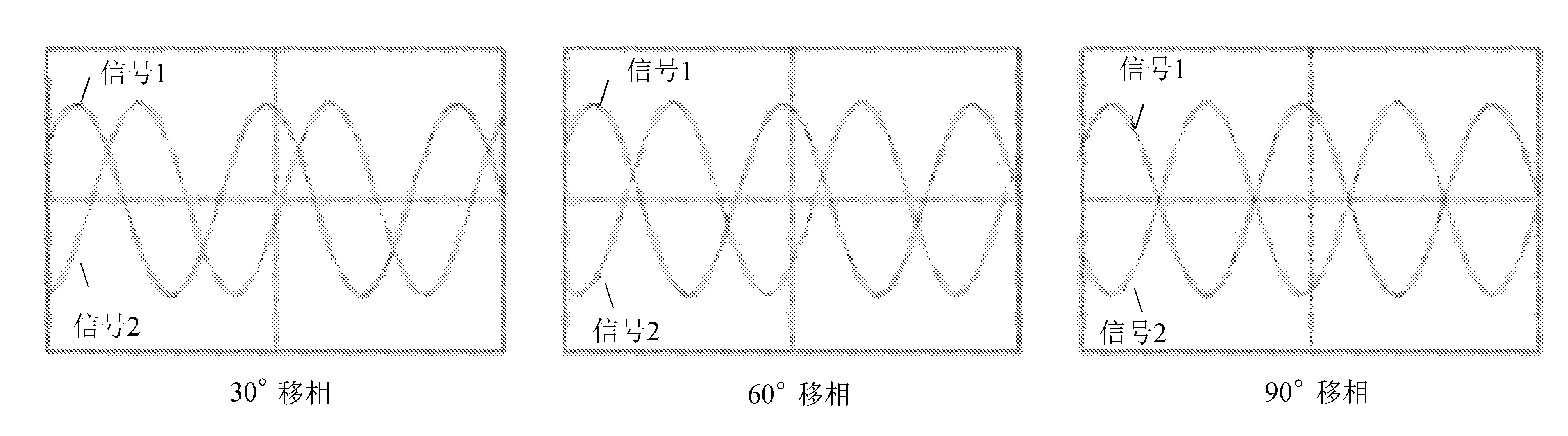
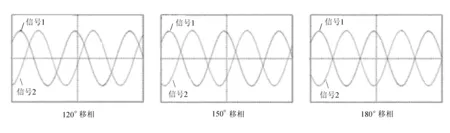
3.2 测试结果及应用
4 结 语

