飞机移动生产线物料配送与空箱回收集成建模

陆志强， 曾 浚

(同济大学 机械与能源工程学院， 上海 201804)

飞机移动装配生产线近年来开始逐步运用于飞机的生产，对于实现装配的稳定性、提高装配效率具有重要的意义.在移动装配生产线上，飞机以缓慢且平稳的速度通过生产线，同时完成各工位所对应的装配作业，通过调整装配线的速度以适应生产节拍的变化.飞机装配过程复杂，其所需的零部件种类繁多，物料配送延迟会导致整条装配线的延期[1-2].飞机装配作业所需物料的配送是实现移动生产线稳定运作的关键环节，因此对其物流配送系统的调度也有极高要求.

飞机装配作业所需物料主要分为三类：数量少、形状不规则的大型结构件，如发动机等；需求量较大、体积小的通用标准件，如螺钉螺母等；种类多、体积中等的装配件，如仪表等.大型结构件由于线边存储容量有限，采用准时化的方式进行配送；通用标准件由于需求量较大且易于暂存于线边，采用线边存储(line stocking)的方式，且通过定期配送实现补货；体积小、种类多的装配件，由于零部件间组装的相关性，采用齐套(kitting)的方式进行配送.本文主要考虑装配件的供应，采用标准料箱进行配送.

多载量小车(tow-train)以循环配送的方式将料箱配送至相应的线边空间，同时考虑将空箱回收至仓库以减少对线边空间的占用，从而提高线边空间的利用率.为了以尽量少的运输次数以满足物料供应需求，兼顾线边空间约束，协调空箱的回收是关键.与一般装配线物料配送问题的主要区别在于问题中引入了空箱回收因素，问题的优化不仅需要安排装配作业所需物料的配送时间，还必须同时对空箱的回收时间进行决策.因此，可认为是一类集物料配送与空箱回收问题于一体的联合决策问题，本文将这一问题称之为飞机移动生产线物料配送与空箱回收集成决策问题(integrated material delivery and container pickup problem for aircraft moving assembly line, IMDCP-AMAL).

现有文献中关于汽车装配线的物料配送问题的研究对于本文具有一定的借鉴意义.Boysen等[3]总结了混流装配线的物料配送方式：循环(milkrun)配送和点对点配送.Souza 等[4]研究装配线准时化物料配送问题，采用不同尺寸的料箱将物料点对点配送至装配线，以最小化搬运费用和库存费用为目标，并提出了具有贪婪随机自适应搜索的启发式算法.Cunha等[5]研究装配线的物料供应问题，对物料的配送批次和频次进行集成决策，基于提出的整数规划方法并通过分支定界算法得到上界和下界.Emde等[6]研究了milkrun的配送方式下，以最小化线边库存水平为目标建立数学模型，证明其为NP完全问题，提出了基于分解算法的禁忌搜索算法.Boysen等[7]研究在配送能力约束下，从仓库将物料组批配送至单一工位，以小车最少出行次数为目标函数建立数学模型，并证明其为NP-hard问题.Golz等[8]研究汽车混流装配线配送问题，基于准时化原则，构建了以最小化小车数量为目标函数的数学模型并设计了两阶段启发式算法进行求解.Fathi等[9]拓展了装配线的小车的调度问题，以最小化出行次数和线边库存为目标，建立了多目标混合整数规划模型，并提出了改进的模拟退火算法用于解决实际问题.针对飞机移动生产线的物料配送问题，胡鑫铭等[10]引入了物料在飞机移动生产线线边的存储决策，构建了物料配送与线边存储集成决策的数学模型，并设计了一种以免疫算法为框架的启发式算法进行求解.朱永国等[11]考虑了飞机装配工位物料需求时间的模糊化现象，建立了基于正态模糊时间窗约束的装配物料配送路径规划的数学模型，并采用遗传算法进行求解.

综上所述，现有文献研究的重点大多集中于物料配送问题，而缺少对物料配送与空箱回收相整合的研究.但在实际飞机移动装配过程中，同一时刻可能存在多项并行装配的作业，且装配作业的时间长，因此线边空间的占用率高.由于线边空间的容量限制，物料配送的决策需要权衡线边空间资源.通过空箱的回收释放被占用的线边空间，以协调配送的调度.若将物料配送和空箱回收分为两阶段进行独立决策，则小车的运载能力不能得到充分利用.同时，由于线边空间的约束，物料配送时间与空箱回收时间相互影响，因此通过联合决策可以为物料配送和空箱回收提供更有效的协同性计划，保证生产线的顺畅运转，具有较高的理论研究意义.

因此，在分析现有文献中相关研究成果的基础上，本文所提出的IMDCP-AMAL问题，基于飞机实际生产背景，以飞机移动生产线的一个装配节拍为决策周期，在仓库与线边存储区域间以循环运输的方式完成装配所需物料与空箱的回收，建立以最小化小车出行次数为目标函数的数学模型，优化决策物料与空箱的组批方式及相应的配送/回收时间.针对上述问题，提出并建立相应的数学模型，并设计了以遗传算法为框架的启发式算法(CHBG)对模型进行优化求解.最后通过数值实验验证所提出算法在求解该问题时的有效性.

1 问题描述及数学模型

1.1 问题描述

飞机移动生产线配送与回收集成问题，是通过优化决策小车对各作业的物料配送时间、空箱回收时间，以协调各作业的物料的配送及其空箱的回收，达到以最少的小车出行次数完成配送与回收任务的目标.图1所示为飞机移动生产线的物料供应模式.IMDCP-AMAL问题的假设与说明如下：

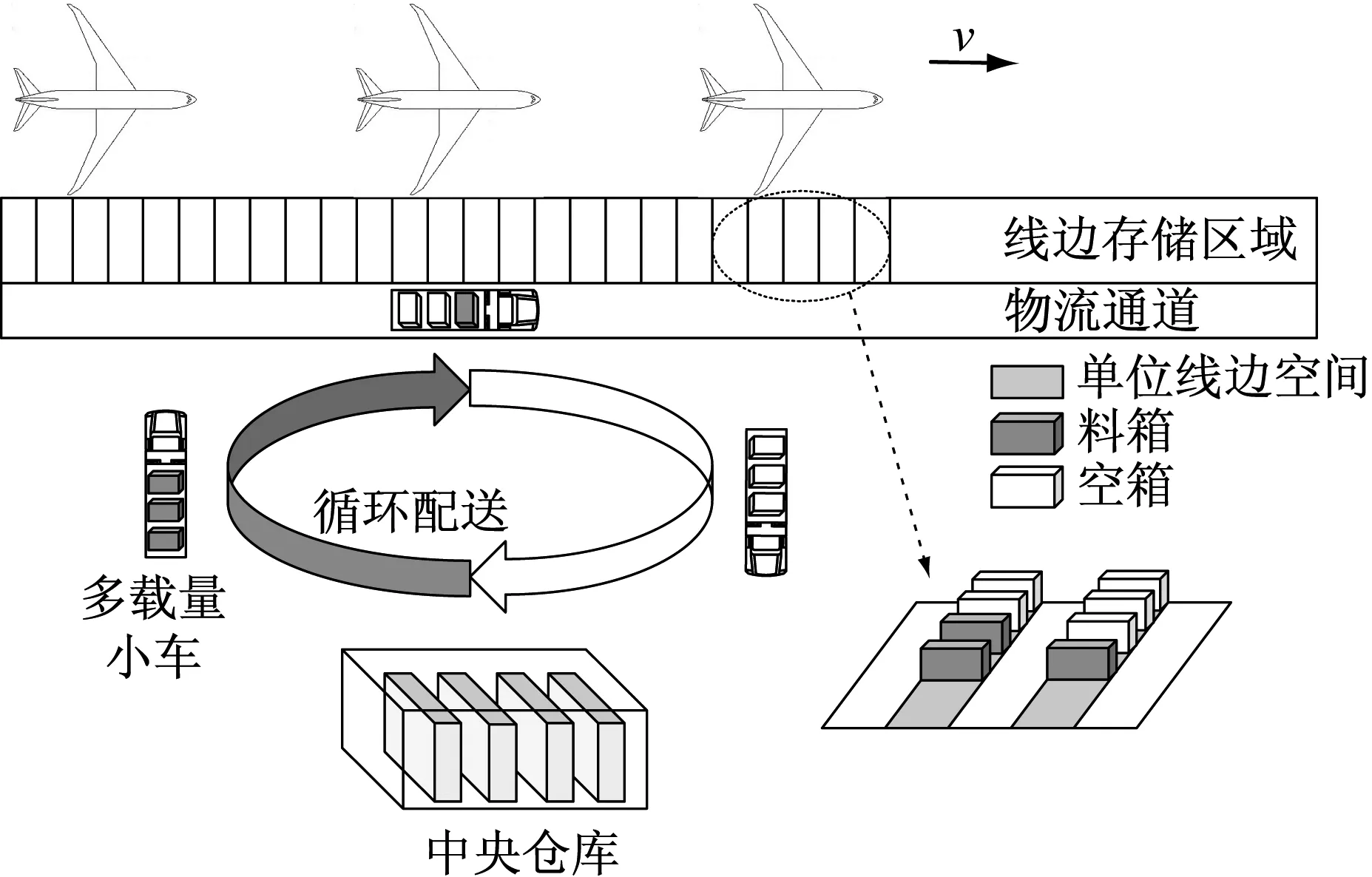
图1 飞机移动生产线物料供应模式Fig.1 Schematic of material supply mode for aircraft moving assembly line

(1) 飞机移动装配项目包含n项作业，J={1,2,…,n}.任意j∈J的执行工期为tj，开始时间为Tjs,完成时间Tjf=Tjs+tj.装配作业所需物料的供应包含两类任务，即送料任务和回收任务.j′∈α={1,2,…,n}表示送料任务集合，包含n项任务，表示将作业j′∈J所需物料配送至相应的线边空间.j″∈β={n+1,n+2,…,2n}表示回收任务集合，包含n项任务，表示将作业(j″-n)∈J的空箱回收至仓库.

(2) 将时间离散化，时间集合为T={1,2,…,ϑ}，ϑ表示计划期时长，任意t∈T表示离散的时间节点.

(3) 线边存储区域是工位旁用于暂存提前送达的料箱和未及时回收的空箱的区域，将线边存储区域离散为单位线边空间，l∈L={1,2,…,w}表示单位线边空间位置集合，且l的最大容量为Cmax.假设作业j的物料的线边暂存位置为lj，lj∈L.任意线边单元l被分配暂存的作业集合为Ωl，Ωl⊂J.对任意线边位置e,f∈L，Ωe∩Ωf=φ.

(4) 作业j所需的物料量为mj，由多载量小车配送至相应的线边空间.某项作业所需的所有物料由一辆小车一次性完成配送，且一辆小车每次可配送多个作业所需的物料，小车的最大容量为Dmax.为了保证作业j的正常进行，其物料的配送完成时间Tjd≤Tjs.作业结束后空箱可以被回收，即空箱的开始回收时间Tjc≥Tjf.因此作业j占用线边空间的时间为料箱送达线边空间的时刻至空箱被小车回收完成的时刻.任意作业的所有空箱由一辆小车一次性完成回收，且一辆小车一次可回收多个作业的空箱.

(5) 物料配送与空箱的回收采用milkrun的方式.R表示小车出行次数集合，k∈R={1,2,…,r}.小车从仓库出发，沿着给定路径行驶并在相应的线边单元对物料箱或空箱进行装卸，然后返回.小车从仓库到线边空间l的行车时间为tl，小车卸载料箱和回收空箱的时间分别为tun,tc.假设作业j的物料配送完成时间为料箱卸载完成的时间.

1.2 数学模型

(1) 决策变量：τk为整数变量，表示第k次出行的发车时刻；Zjk为0，1变量，当其为1时表示作业j所需物料在第k次出行时配送，否则为0；Yjk为0，1变量，当其为1时表示作业j的空箱在第k次出行时回收，否则为0.

(2) 目标函数：

minZ=|R|

(1)

约束：

(2)

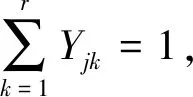
(3)

τk+1≤τk+1,∀k∈R

(4)

(5)

∀k∈R,l∈L

(6)

∀k∈R,l∈L

(7)

∀k∈R,l∈L

(8)

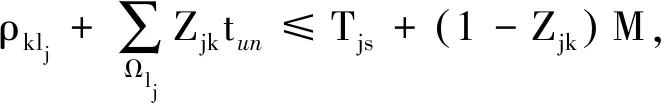
∀k∈R,j∈J

(9)

(10)

τk,∀k∈R

(11)

Zjk∈{0,1},Yjk∈{0,1},∀k∈R,j∈J

(12)

其中，式(1)为目标函数，即最小化多载量小车的出行次数；式(2)表示任意装配作业的料箱必须一次性配送至相应的线边空间；式(3)表示表示任意装配作业的空箱必须一次性回收至仓库；式(4)定义了多载量小车出行次数的先后顺序约束；式(5)表示每次安排配送的料箱总量不得超过小车的最大容量；式(6)表示小车离开任意线边位置时的运载量不超过小车的最大容量；式(7)定义了小车到达线边位置的时间；式(8)表示安排入任意单位线边空间暂存的料箱量不得超过线边空间的最大容量；式(9)表示任意作业的物料的配送完成时间应不晚于其装配开始时间，其中M为无穷大的数；式(10)表示任意作业的空箱的回收开始时间应不早于其装配完成时间；式(11)和式(12)定义了决策变量的可行域.

2 算法设计

针对IMDCP-AMAL的特点，设计了一类以遗传算法为框架的启发式算法(CHBG)，其中嵌套了局部搜索算法.该算法的基本框架与主要思路为：通过遗传算法较强的全局搜索能力搜索较优的任务(送料、回收)执行顺序，为每一条包含任务执行顺序的染色体设计有效的解码过程对小车装载能力进行合理分配，从而获得各项作业的物料配送时间、空箱回收时间的可行解.在此基础上，基于上述结果，通过深度局部搜索算法对配送与回收任务进行再分配，使得更多的任务能并行完成，进一步减少小车出行次数.以下分别对遗传算法框架、约束转换、启发式解码以及局部搜索算法进行阐述.

2.1 算法框架

遗传算法采用任务列表方式编码，染色体由任务列表λ组成，每一个基因位表示一个任务序号，则每一条染色体代表一个任务顺序列表.一个任务列表包含所有的送料任务和回收任务的执行的优先顺序.染色体的初始化方式包括随机生成和基于优先规则生成两种，优先规则包括最小冗余度任务优先、最小最早离开时间任务优先、最大最早离开时间任务优先、最小最迟离开时间任务优先、最大最迟离开时间任务优先.遗传算法的进化算子可以参考文献[12-14],本文不再赘述.

设定遗传算法的种群大小为P，迭代次数为N，λ表示当前代数.适应度函数Fit如式(13)所示，表示小车装载率平方的均值，用于评估小车装载量的利用.CHBG算法的目标为最大化染色体个体的适应度值.

(13)

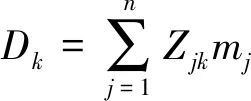
算法框架如图2所示.对每个染色体个体，首先进行约束转换，然后通过启发式解码得到可行解，最后利用深度局部搜索进行优化.

图2 遗传算法框架Fig.2 Genetic algorithm framework

2.2 约束转换

在求解IMDCP-AMAL问题时，通过将线边空间的容量约束转换为任务的完成时间约束，以松弛约束，便于问题的求解.

为了保证装配作业j的正常执行，其对应的送料任务j′的最迟完成时间L等于Tjs，回收任务j″的最早完成时间Ej″等于Tjf.送料任务的初始完成时间dtj∈[0,Tjf]，回收任务的初始完成时间ctj∈[Tjs,T].则作业j的料箱(物料及空箱)在线边空间的占用时间窗为[dtj,ctj]，由送料任务的完成时间和回收任务的完成时间共同决定.在计划期内，任意时刻的料箱占用量不超过线边空间的容量.因此，通过约束送料任务j′的最早完成时间和回收任务j″的最迟完成时间可实现线边空间容量的限制.转换方式举例说明如下：

图3所示为某线边位置所分配的所有作业的调度计划.该线边位置所分配暂存的作业集合为Ω={1,2,3,4}，Cmax=5.作业1、2、3的料箱在线边空间占用的绝对时间窗交集为Α=[6,7]，作业4的料箱在线边空间占用的绝对时间窗为B=[12,17].Con表示某时刻线边空间的初始占用量.对任意t∈(3,10),Con+m1>Cmax，为了保证线边空间容量约束，则Α∩Β=Ø.因此，若先安排作业4所对应的送料任务，其最早完成时间E4″为7，作业1、2、3中所对应的回收任务min{Lj″|j″=1,2,3}min{ctj|j=1,2,3}.

图3 调度计划甘特图Fig.3 Gantt chart representation of schedule

2.3 启发式解码

基于确定的任务优先顺序，综合考虑物料配送能力和线边空间存储能力为各项任务安排完成时间.本文设计启发式方法对染色体(编码)进行解码.具体决策方法如下：在安排某次小车出行时，首先根据任务列表顺序选择某个未完成任务，安排该任务在此次出行中完成从而确定小车出行的时间窗.然后通过两阶段启发式算法决策送料任务与回收任务，不断调整小车出行时间.其中，第一阶段，与回收任务协调，优先安排线边位置靠前的送料任务；第二阶段，借鉴文献[13]的FFD(first-fit-decreasing)启发式规则安排回收任务.若小车空间约束不满足，则开始下一次出行的安排.通过依次安排小车每次出行所完成的任务，获得完整的配送与回收计划.启发式解码的具体步骤如下：

(1) 令k=1，初始化已安排任务集合ω=Ø，未安排任务集合η={1,…,2n},未安排的送料任务集合D={1,…,n}，未安排回收任务集合Ρ={n+1,…,2n}.

(2) 初始化第k次出行已安排任务集合υk=Ø，送料任务集合Dk=Ø，回收任务集合Pk=Ø.

(3) 可选择的任务集合ωk=η.读取编码中的任务列表.

(4) 按照顺序从小到大选择序号最小的任务b∈ωk，以任务b确定小车离开时间窗[εA,ψA].

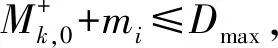
(10) 令k=k+1，若η≠Ø，转(2)，否则转(11).

(11) 检验单位线边空间容量约束，即计划期T内任意时刻所有线边空间的料箱数都不超过上限，若不满足，则k=k+ζ，ζ为惩罚因子.

(12) 输出配送回收计划S，算法结束.

2.4 局部搜索

局部搜索算法以启发式解码得到的可行出行计划作为初始解，将小车单次出行的任务集作为搜索对象，判断该集合中每个任务可于其他某次出行中完成的情况.若所有任务均可实现转移，则将此次出行的全部任务分配至其他出行中完成，以达到减少整体出行次数的目的.算法的具体步骤如下：

(1) 获取可行计划S，由一组元组(Θ,λ)∈S表示，Θ代表每次出行安排的任务集合，λ代表小车出行时间.

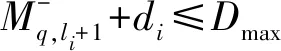
(4) 若所有更新的q满足时间约束，则|R|=|R|-1.

(5) 通过调整出行时间使线边空间容量约束满足，若能满足，则更新计划S，转(2)，否则转(6).

(6) 输出优化后的计划S.

3 数值实验

本文算法运用C#(Visual Studio 2015)编程实现，测试实验在Internet Core i7处理器，3.4 GHz主频，8G内存的测试平台上进行.测试算例基于PSPLIB算例库，根据IMDCP-AMAL的特点对数据进行扩充，为装配作业数量为16、18、20、22、24、30、45和60八类规模的数据，分别生成30组算例.同时为算例中每个作业j生成l∈(1,10)的线边存放位置，随机生成m∈(1,5)的物料需求量.设定多载量小车从仓库到第一个线边位置的行车时间t1=4，到第l个线边位置的行车时间tl=tl-1+1,∀l=2,…,w，停留时间tun=2,tc=2.多载量小车配送能力上限Dmax=5，单位线边空间容量上限Cmax=5.

3.1 与CPLEX的对比

通过表1可以得出，在小规模算例实验中，CHBG算法在可接受的时间内能够求得较优的结果.对于大多数算例规模为16和18的作业，CHBG算法求得的解与CPLEX得到的结果GAP值不超过5%.随着算例规模以及复杂度的增加(算例规模为20～24)，CPLEX在许多情况下无法求得最优解，而CHBG算法仍可求得较优解.

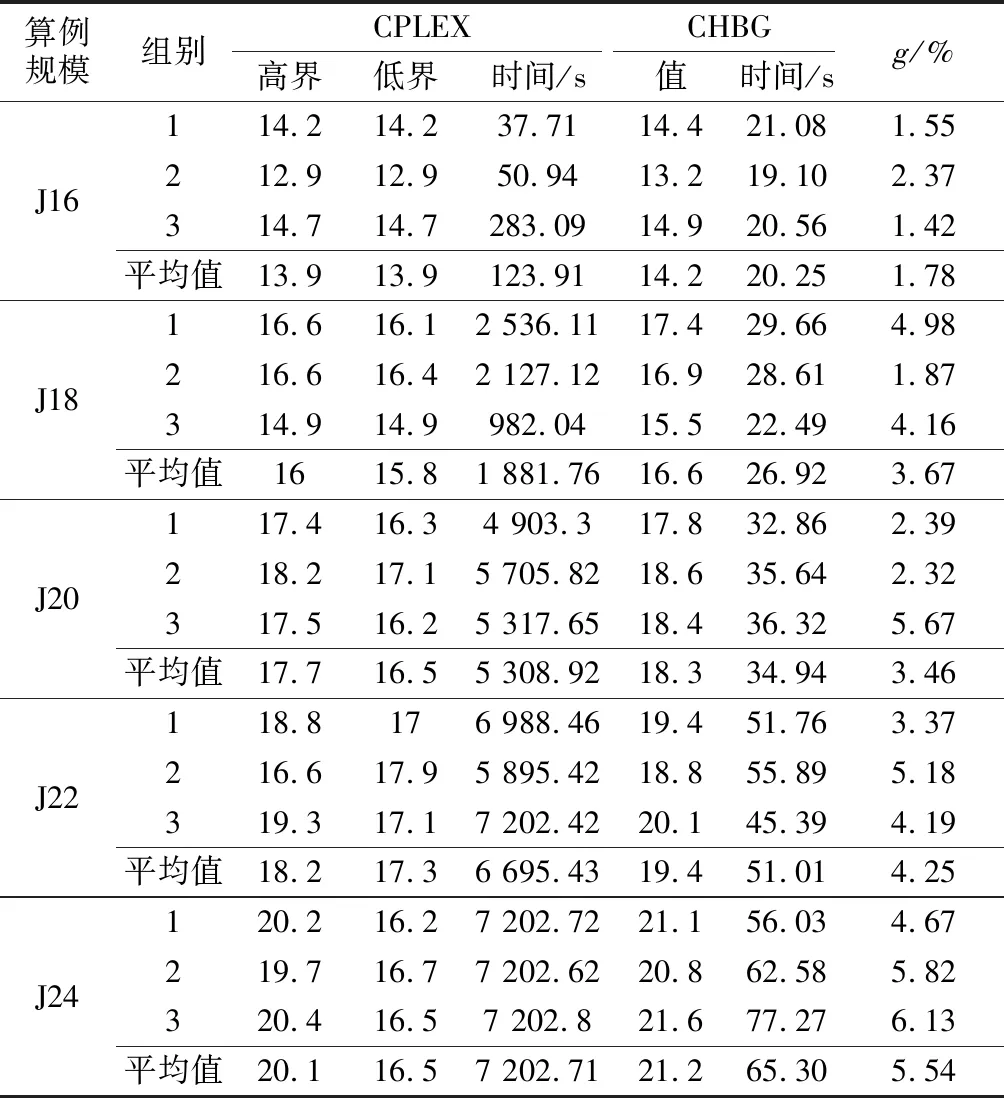
表1 小规模算例实验结果Tab.1 Numerical experiment results of small- scale examples

3.2 与现有文献的对比

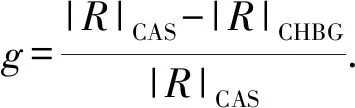
通过表2可得出，在求解大规模算例时，CHBG集成算法在可接受的时间内能够求得较优的结果.对于大多数算例规模为30的作业，而CHBG算法求得的解相对于CAS的优化比例达到25.6%，随着算例规模以及复杂度的增加(算例规模为45和60)，CHBG算法的优化比例也在4.82%以上.说明将物料配送和空箱回收综合考虑进行集成决策相比传统的独立决策方法具有优势.

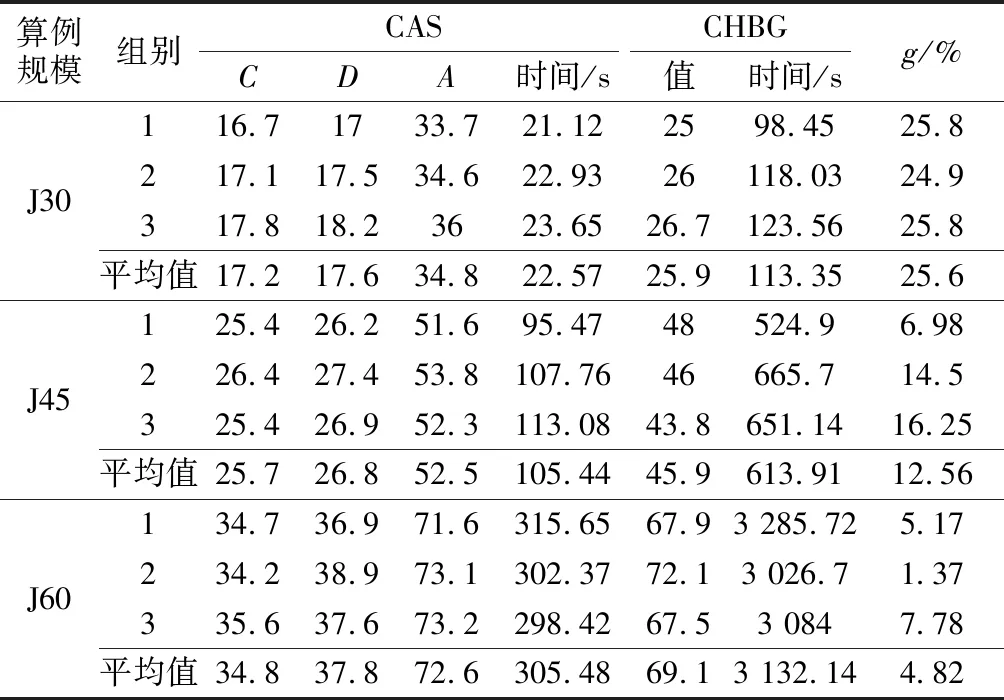
表2 大规模算例实验结果Tab.2 Numerical experiment results of large- scale examples

4 总结与展望

(1) 以飞机移动生产线为实际背景，同时考虑了物料的配送及其空箱的回收问题，将这两类相互影响的决策整合到一个联合决策框架中，提出了集成决策的优化模型.

(2) 针对集成模型设计了以遗传算法为框架的启发式算法，该算法对小车的装载、调度进行了联合优化决策，通过充分利用小车运载能力优化了小车出行次数，减少了配送与回收的总成本.

(3) 通过数值实验对算法进行了验证，实验结果证明了本文提出的算法的有效性，为飞机移动生产线这类考虑空箱回收的物料配送问题研究提供了借鉴.

(4) 后续可以考虑对飞机移动生产线中线边空间物料摆放决策展开详细研究，为IMDCP-AMAL问题提供更高效的决策.