海绵城市低影响开发设施多目标优化设计
陶 涛, 肖 涛, 王林森, 颜合想
(同济大学 环境科学与工程学院, 上海 200092)
在全球范围内,气候变暖导致年平均降雨量增加,尤其是极端暴雨天气更加频繁[1].同时我国城市的迅速发展导致不透水表面比例不断增加,城市地表所产生的径流量激增,使得城市区域的内涝风险增加[2].为应对日益严重的城市内涝及降雨所导致的污染问题,20世纪90年代末,美国提出了一种新的暴雨管理技术,即低影响开发(low impact development, LID)技术.低影响开发理念旨在源头运用分布式的小型化技术尽量维持场地开发前的水文状况,包括径流总量、峰值流量以及峰值出现的时间,从而减少开发区域的不透水面积,减少径流对周边水系的污染.关于低影响开发优化设计的研究如Giacomoni[3]运用第二代非支配排序遗传算法优化了雨水花园、绿色屋顶、植草沟的设计参数和空间布局; Zhang[4]则将美国环保署提供的SWMM模型与多目标优化算法相结合,提出了低影响开发技术方案优化框架,该框架以生物滞留单元和透水铺装为研究对象,以总费用和径流总体积为目标函数,以开发前的峰值流量为约束条件,并成功将该技术框架运用于工程实例.
在我国,低影响开发技术研究还处于初步阶段,其规划、设计、评估、管理等方面的认识有待完善,尤其是结合优化算法对低影响开发设施进行优化设计方面的研究极其有限,对于如何确定一片区域需要设置的雨水设施规模、如何选取雨水设施组合方式的研究则存在空白.本文以透水铺装和生物滞留单元两种低影响开发雨水设施为研究对象,着重解决在一片研究区域上如何设置低影响开发雨水设施的规模,从而使付出的成本最低,得到的效益最高.
1 低影响开发多目标优化设计模型构建
本文以低影响开发的总费用和年径流总量控制率为目标函数,以低影响开发设施的面积为约束条件,构建低影响开发设施的多目标优化设计模型,以求得不同规模的低影响开发设施的优化方案.模型设计及求解路线如图1所示.

图1 低影响开发多目标优化Fig.1 Schematic diagram for low-impact development multi-objective optimization
1.1 年径流总量控制率
1.1.1设计降雨量的计算
设计降雨量是各城市实施年径流总量控制的专有量值.在某一块区域的低影响开发设计过程中,低影响开发技术措施的规模可通过容积法、流量法或水量平衡法进行计算.以下渗和调蓄功能为主的低影响开发雨水设施(如生物滞留单元)可利用容积法进行计算.对透水铺装等仅以原位下渗为主、顶部无蓄水空间的渗透设施,可通过参与综合雨量径流系数计算的方式确定其规模[5].利用低影响开发设施的规模反推出其所能全部控制的降雨量,参考刘绪为等[6]的研究,并结合上海市降雨经验,采用短历时降雨(2h)进行设计计算.目标区域的设计降雨量可计算如下:
V=10HφF
(1)
式中:V为设计进水量,m3;H为设计降雨量,mm;φ为综合雨量径流系数;F为目标区域面积,m2.
设计进水量V包括有效调蓄容积和下渗量两部分,生物滞留单元的蓄水空间和下渗量应计入设计进水量的计算,透水铺装只改变区域综合雨量径流系数.设计进水量V的计算如下:
V=Vs+Wp
(2)
式中:Vs为生物滞留单元的有效调蓄容积,m3;Wp为生物滞留单元的下渗量,m3.下渗量Wp计算如下:
Wp=KJAsts
(3)
式中:K为土壤渗透系数,m·s-1;J为水力坡度,通常取J=1;As为有效渗透面积,m2;ts为渗透时间,s,指降雨过程中的渗透历时,通常取2 h.
结合式(1)~式(3)可求得设计降雨量如下:
(4)
对于一定面积的生物滞留单元和透水铺装,可通过式(4)计算出相应规模对应的设计降雨量.
1.1.2年径流总量控制率的推求
径流控制率是构建海绵城市的首要控制目标之一.年径流总量控制率是指结合自然过程,通过人为加强的渗透、蒸发等作用以及雨水的及时调蓄储存,使得区域内全年累计的被控制降雨量占全年总降雨量的比例[7].本文收集了上海市1985—2014年间的日降水量数据,根据《海绵城市建设技术指南》对城市年径流总量控制率所对应的设计降雨量的定量方法,推求出上海地区设计降雨量和年径流总量控制率之间的关系曲线(图2).由式(4)计算出的设计降雨量可根据图2推求其对应的年径流总量控制率,具体求解过程由MATLAB实现.
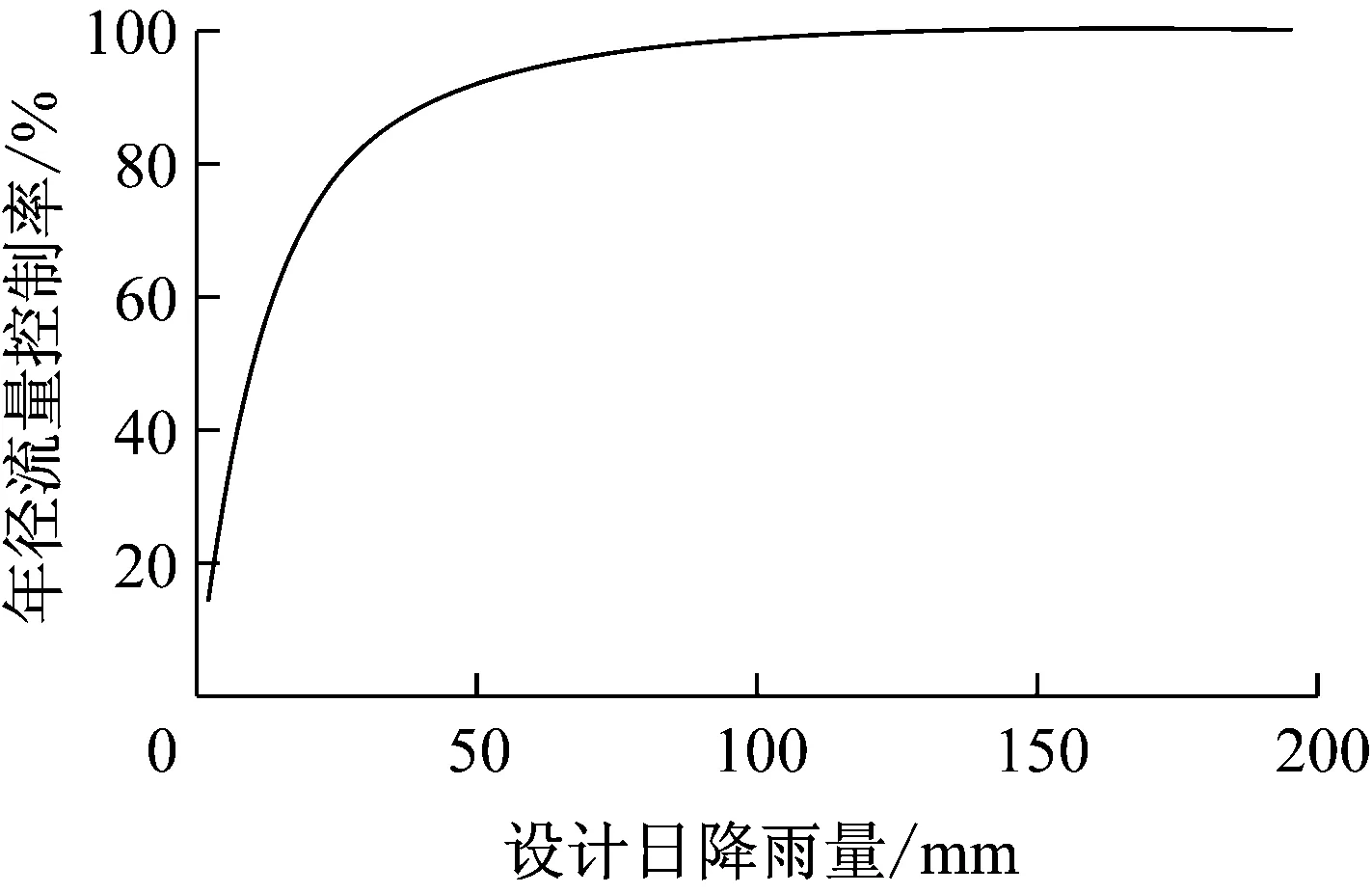
图2 上海市设计降雨量和年径流总量控制率关系曲线
Fig.2ThecurveoftherelationshipbetweenthedesignprecipitationandthevolumecaptureratioofannualrainfallinShanghai
1.2 低影响开发技术总费用
采用全过程生命周期成本(life cycle cost, LCC)来估算低影响开发的总费用,由于国内的低影响开发技术处于起步阶段,工程实践项目较少,缺乏足够的数据积累,此外,土地和人力成本在我国各个城市也存在较大差异.因此,为了尽量减小这种差异同时考虑我国实际情况,仅考虑低影响开发技术的建造成本以及运营和维护成本.
对于同一种低影响开发技术,其建造费用以及运营维护费用与其面积呈线性关系[8].本文采用的低影响开发技术包括透水铺装和生物滞留单元,那么总费用函数可以表示如下:
z=(a+b)×sbrc+(c+d)×spp
(5)
式中:z为低影响开发技术的总费用,元;a为单位面积生物滞留单元的建造费用,元·m-2;b为单位面积生物滞留单元的运营维护费用,元·m-2;c为单位面积透水铺装的建造费用,元·m-2;d为单位面积透水铺装的运营维护费用,元·m-2;Sbrc为生物滞留单元的面积,m2;Spp透水铺装的面积,m2.
1.3 约束条件
在实际工程中,能够进行低影响开发或改造的面积是有限的,因而该问题的主要约束条件为面积的限制.对于生物滞留单元,可根据研究区域的绿化面积确定生物滞留单元所能设置的面积的上下限.而对于透水铺装,仅适合人行道、广场及部分道路,可根据研究区域三者的比例确定透水铺装设置面积的上下限,约束条件如下:
(6)
式中:Abrc为研究区域能够设置生物滞留单元的面积的上限,m2;App研究区域能够设置透水铺装的面积的上限,m2.
2 模型求解
非支配排序遗传算法(Non-dominated Sorting Genetic Algorithms, NSGA)是Srinivas和Deb在20世纪90年代提出的一种多目标优化算法[9].NSGA算法在基本遗传算法的基础上,对如何筛选个体作为下一代父本进行了改进:将每个个体相互比较从而得出他们的支配与非支配关系,并据此对每个个体进行分层,然后再对每个个体做出选择,从而找出更优的解.由于NSGA算法的计算复杂且容易使最优解丢失,Deb等人随后又提出第二代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithms Ⅱ, NSGA-Ⅱ)[10],提出了快速非支配排序方法,引入精英策略,采用拥挤度来表示每个个体在种群中的适应度,使NSGA-Ⅱ具有更快的计算效率和鲁棒性.NSGA-Ⅱ算法一般过程如下:
(1) 首先在可行解域内产生个体规模为N的初始种群P0;
(2) 对初始种群进行交叉和变异操作产生N个子代;
(3) 将N个父代和N个子代合并,并进行非支配排序和计算拥挤度;
(4) 根据每个个体的非支配排序等级和拥挤度选出N个个体组成新的父代种群P1;
(5) 重复过程(2)~(4),直到遗传代数满足设定的要求.
NSGA-Ⅱ算法流程如图3所示.NSGA-Ⅱ对于解决多目标优化问题是一种有效的解决方法,但算法本身的参数对结果有着很大的影响.在应用该方法解决问题时,需要合理的设定种群规模、遗传代数、交叉和变异操作的概率以保证最终获取的曲线接近于Pareto最优,在每一步交叉和变异操作过程中应当考虑新生子代是否满足约束条件.
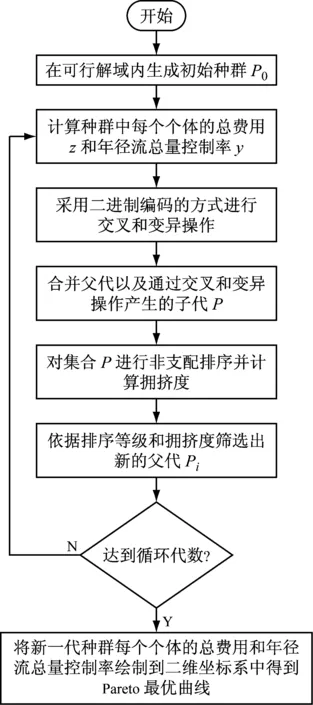
图3 年径流总量控制率与总费用优化算法流程Fig.3 Optimization algorithm flow chart of the volume capture ratio of annual rainfall and total cost
3 工程案例
以上海市西部某片区为研究实例,服务面积2.63 km2.研究区域总体的绿化率40%,硬化路面占总面积的60%,绿化面积径流系数为0.15,硬化路面径流系数为1.0,决定在该片区中建设生物滞留单元和透水铺装两种LID基础设施,上海地区生物滞留单元和透水铺装的建造成本见表1和表2.

表1 生物滞留单元单位面积建造成本Tab.1 Construction cost of bioretention per unit area

表2 透水铺装单位面积建造成本Tab.2 Construction cost of permeable pavement per unit area
结合芦琳[11]、韩松磊[12]的研究成果以及上海市的物价,根据表1和表2所提供的数据,计算出生物滞留单元的单位面积造价为470~613元·m-2.透水铺装的单位面积造价为160~226元·m-2.根据陈韬[13]等人的研究,整个生命周期内,生物滞留单元的运营维护成本约为其建造成本的8.5%,透水铺装的运营维护成本约为其建造成本的5%.取建造成本的下限构建费用函数,即单位面积生物滞留单元的建造费用为470元·m-2,运营维护费用为40元·m-2,单位面积透水铺装的建造费用为160元·m-2,运营维护费用为8元·m-2.
LID设施的参数设置参照SWMM模型用户手册[14],生物滞留单元蓄水层厚度取300mm,孔隙比取0.6,渗透系数K取1.51×10-5m·s-1,透水铺装的径流系数取0.2.当每种低影响开发雨水设施的设计参数确定后,设计降雨量可以认为仅是面积函数,利用式(4)可求得该区域不同LID设施面积对应的设计降雨量,然后利用图2可计算相应的年径流总量控制率.上述两个目标函数可表示为
minz=(470+40)×sbrc+(160+8)×spp
maxy=f(sbrc,spp)
式中:y为研究区域年径流总量控制率.
在确定约束条件和目标函数的各参数后,通过利用MATLAB 编写非支配排序遗传算法程序,从而得到一系列的Pareto 解集.选取遗传算法中的参数:种群个数N=1 000、遗传代数G= 50,交叉概率采用0.8,变异概率采用0.3.经过优化计算,可以求出一系列的Pareto 解集.其运行结果见图4.图4表示经过50次迭代后的非支配个体(每个个体代表着一种LID方案)的年径流总量控制率和总费用,非支配种群构成了一条Pareto最优曲线.
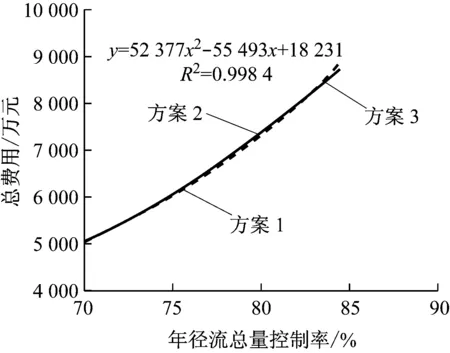
图4 年径流总量控制率与总费用的Pareto最优曲线Fig.4 Pareto optimal curve of the volume capture ratio of annual rainfall and total cost
从图4中可以看出,年径流总量控制率与总费用的函数关系可用二次函数拟合,拟合系数为0.998 4,该拟合曲线可用于研究区域估算要达到某一年径流总量控制率下需要的生物滞留单元和透水铺装的最低总费用,曲线上每个Pareto 点均对应一种最优的低影响开发设施规模,各种最优的解集可为设计决策者提供多种决策选择方案.根据《海绵城市建设技术指南》提供的我国大陆地区年径流总量控制率分区图,上海市属于Ⅲ区,即上海市合理的年径流总量控制率在75%~85%之间.按照前述要求,表3列出了3种具有代表性的LID布置方案,这3种方案均为最优方案,但3种方案设计规模不同,因而具有不同的年径流总量控制率和总费用.方案1中在研究区域内共设置生物滞留单元2 920个,透水铺装单元6 000个(每个LID单元面积为25 m2),此规模下能完全控制的降雨量为23.1 mm,对应的年径流总量控制率为75.9%,所需的总费用为6 240.4万元.其余方案的详细信息见表3.
如表3所示,优化设计后的方案1~方案3的年径流总量控制率依次提高,随之产生的总费用也增加,即LID方案的经济性与径流控制指标不可兼得.当决策者由于资金紧缺看重LID方案的经济性时,可选择方案1,在满足径流总量控制目标时总费用最

表3 3种代表方案的年径流总量控制率以及总费用Tab.3 The volume capture ratio of annual rainfall and total costs of the three representative programs
少;当决策者强调LID方案的径流总量控制目标时,可选择方案3以达到最佳的年径流总量控制率;当决策者希望在经济性和径流总量控制目标之间找到一个平衡时,可选择方案2.具体选择哪种优化方案,视决策者的投资能力和径流总量控制要求而定.
由图4可知,该费用与年径流总量控制率近似的满足二次函数关系,当年径流总量控制率达到某一标准时,若一味的提高年径流总量控制率,所需要的LID方案总费用会迅速增加,如当年径流总量控制率从75%提高到80%时,所需的总费用增加了1 284.6万元;而当年径流总量控制率从80%提高到85%时,所需的总费用却增加了1 546.5万元.
4 结论
提出了一种优化LID方案的数学模型,以年径流总量控制率和总费用作为目标函数,利用NSGA-Ⅱ算法优化低影响开发项目的面积,同时兼顾了经济性和规划控制目标.通过实例分析表明,提高年径流总量控制目标,会使LID方案的总费用增加,当年径流总量控制率超过一定值时,投资效益会急剧下降;得出了该区域低影响开发的Pareto 最优曲线,利用二次函数进行拟合,简单直观;提出3种不同规模的LID 方案供决策者选择,避免了常规决策的主观性和不确定因素,使决策者能根据实际情况选择合适的优化方案.

