格构拱结构动力响应评估的改进模态推覆分析法

曲 扬， 罗永峰， 黄青隆， 朱钊辰

(同济大学 土木工程学院，上海 200092)

近年来历次强震都表明，许多结构震害都有竖向地震作用的痕迹，甚至不乏由其直接导致的震害，例如汶川地震中强烈的竖向地震分量对一些大跨度结构造成了严重破坏[1-4]，因此，在大跨度结构抗震设计中，必须重视竖向地震作用引起的结构动力响应[5].

在诸多大跨度结构体系中，格构拱由于材料利用率高、施工方便等优点，广泛应用于火车站屋盖等大跨度结构中.目前，格构拱结构在罕遇地震下的弹塑性地震反应多采用时程分析(RHA)方法[6]和静力推覆分析(SPA)方法[7]进行计算，相较于前者，SPA方法既可以考察结构的弹塑性力学行为，满足性能化抗震设计多阶段、多水准的要求，又能够大大节省运算成本，因而广泛应用于大跨度结构弹塑性地震反应的预测和评估[8-9].

已有国内外学者对静力推覆分析方法用于评估大跨度结构在竖向地震作用下动力响应的适用性进行了研究.钱稼茹等[10]对国家体育场大跨度钢结构进行罕遇地震下的推覆分析，指出采用现有SPA方法难以实现大跨度钢结构竖向地震响应评估.杨木旺等[11-12]沿用SPA方法的思路，建立了评估大跨度空间结构竖向抗震性能的Pushdown(推倒)方法，但该方法难以应用于格构拱一类水平和竖向位移耦合显著的结构.相阳、罗永峰等[13-14]基于模态推覆分析方法提出了EMPA方法，该方法初步解决了水平地震作用下格构拱结构的位移耦合问题，但未能应用于竖向地震作用下的结构响应评估，且仅考虑了一阶振型的影响.Ohsaki等[15]针对大跨度格构拱结构提出了一种多模态线性组合的推覆分析方法，虽然考虑了位移耦合和多阶振型，但多次组合模态进行推覆分析的方法，既缺乏物理意义解释，也丧失了简洁性.因此，关于大跨度结构在竖向地震作用下的动力响应评估，现有SPA方法仍无法兼顾解决位移相互耦合显著、推覆曲线特征节点难以选取、低估多阶振型及其组合方法的影响等问题，其根本原因在于原本适用于多高层结构的SPA方法，难以直接应用于振型密集且复杂、位移耦合显著、荷载-位移关系不够直观的大跨度结构.

针对上述问题，本文基于静力稳定分析中特征刚度[16-17]的概念，提出适用于评估大跨度格构拱结构在竖向地震作用下动力响应的改进模态推覆分析(IMPA)方法及其计算步骤，该方法基于特征刚度建立了等效单自由度体系，避免了推覆曲线选点的问题，并推导出推覆荷载公式，通过两阶段推覆分析考虑位移耦合与多阶振型的影响.选取一个大跨度格构拱结构，对结构分别在硬土和软土场地若干条竖向地震波激励下的动力响应进行计算，并与RHA方法进行对比，以验证IMPA方法的适用性与实用性.

1 基于特征刚度的IMPA方法基本理论

1.1 第一阶段推覆分析与ESDOF体系

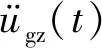
(1)

式中：u(t)为由于竖向地震作用产生的结构体系动力位移向量；M和C分别为结构体系的广义质量矩阵和阻尼矩阵；lz为竖向影响因子.Fs(t)为结构体系恢复力向量，与当前变形状态和加载历史相关.

将线性体系模态分解方法引入非线性分析中，假定非线性体系的广义动力位移向量可以分解为

(2)

式中：φl和ql(t)分别为第l阶振型的振型向量和广义振型坐标.

(3)

(4)

取qn(t)=ΓnDn(t)，考虑到振型参与系数Γn=Ln/Mn，整理得

(5)

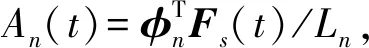
为通过推覆分析得到An-Dn的关系，需要建立ESDOF体系.引入结构静力稳定分析中的结构特征刚度k*，该参数可表征结构的整体刚度，反映结构抵抗变形的能力.在对结构进行加载分析的过程中，第j荷载步的特征刚度为

(6)

式中：KT,j、ΔUj和ΔFj分别为第j荷载步切线刚度矩阵、位移增量和荷载增量.

在线弹性阶段，与第n阶竖向振型相关的位移响应可表示为un(t)=φnΓnDn(t)，相应的恢复力为

(7)

对结构进行第一阶段的模态推覆分析，则第j荷载步的推覆荷载Fn,j可表示为

(8)

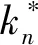
(9)

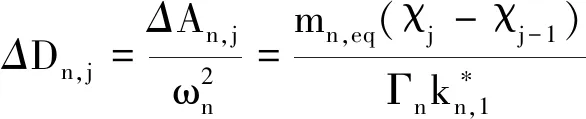
(10)

进入非线性阶段，由于刚度退化，振型已不同于线弹性阶段，但考虑到相互之间耦联性较弱，故而推覆分析第j荷载步的推覆荷载和伪加速度增量仍可用式(8)和式(9)表示，此时定义等效荷载增量ΔFn,j和等效位移增量Δdn,j为

ΔFn,j=mn,eq(An,j-An,j-1)

(11)

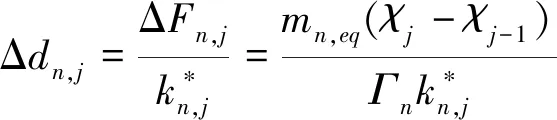
(12)

对比式(10)和式(12)可知，等效位移增量Δdn,j即为振型位移增量ΔDn,j，从而得到了An-Dn关系.

由于重力已在结构中产生了变形，因此，在竖向地震作用下，结构竖直向上和向下的荷载-位移关系不同，即在竖直方向的刚度上下不对称，因此，需对结构按照第n阶竖向振型分别进行竖直向上和向下的推覆分析，得到An+-Dn+和An--Dn-，两者结合即为结构在竖直方向上的An-Dn的关系，从而建立基于特征刚度k*的ESDOF体系，进而通过式(5)求出振型位移响应Dn(t)，代入式(2)即可求出结构总动力位移响应u(t).

1.2 第二阶段推覆分析与推覆荷载

仅取前两阶竖向振型为例.通过对前两阶竖向振型ESDOF进行RHA求解，可得结构总动力位移响应时程为

u(t)=φ1q1(t)+φ2q2(t)

(13)

在重力作用下，结构的响应为ug，则结构总位移响应时程为

ut(t)=φ1q1(t)+φ2q2(t)+ug

(14)

umax=φ1q1(tmax)+φ2q2(tmax)

(15)

为得到目标性能点处的其他响应(如单元应力等)，在重力作用的基础上，以umax为位移模式进行第二阶段非线性推覆分析.为简便起见，取q1=q1(tmax)，q2=q2(tmax)，则umax=φ1q1+φ2q2.

在线弹性阶段，第j荷载步的推覆荷载Pj为

(16)

(17)

(18)

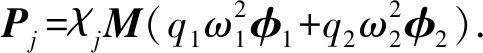
将线弹性阶段的推覆荷载推广到非线性阶段，仍取第j荷载步的推覆荷载为

(19)

一般地，取前n阶竖向振型进行第二阶段推覆分析，其中，第j荷载步的推覆荷载为

(20)

1.3 IMPA方法计算步骤

计算步骤如下：

(1) 进行结构模态分析，选取主振型，确定各阶主振型的荷载空间分布模式；

(2) 根据各主振型的荷载空间分布模式，对结构分别进行第一阶段非线性模态推覆分析，得到各主振型荷载模式下的特征刚度变化；

(3) 基于各主振型的特征刚度，建立对应各主振型的等效单自由度(ESDOF)体系；

(4) 针对对应各主振型的ESDOF进行时程分析，得到各ESDOF的位移响应时程；

(5) 将各ESDOF位移响应时程按振型组合，得到结构整体位移响应时程u(t)；

(6) 取u(t)的最不利位移作为变形模式，以式(20)中的Pj为推覆荷载，对结构整体进行第二阶段推覆分析，得到结构在地震作用下的总响应.

2 数值算例

为验证提出的IMPA方法的适用性，采用ANSYS对一个大跨度格构拱结构进行推覆分析和时程分析，以节点位移、最不利单元应力以及计算耗时作为对比参数，分析IMPA方法的误差和效率.

2.1 格构拱结构模型

结构跨度36 m，矢高12 m，拱厚度1 m，矢跨比1/3，外环节点集中质量0.5 t，内环节点集中质量0.2 t，两端固定铰支座，杆件截面如图1所示，材料为Q235钢，采用双线性随动强化模型，弹性模量206 GPa，屈服强度235 MPa，屈服后弹性模量0.8 GPa.拱结构节点编号为外环节点顺时针1～33，内环节点顺时针34～65.本算例研究结构在竖向地震作用下的动力响应，其竖向主振型信息见表1，振型图如图2所示.

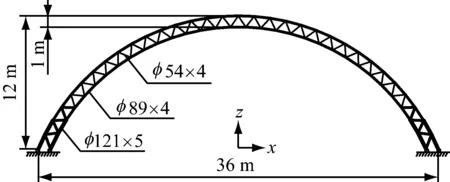
图1 格构拱结构模型及杆件截面(单位：m)Fig.1 Structural layout and member sections of the arch (Unit: m)表1 格构拱结构竖向主振型信息Tab.1 Information of vertical fundamental modes of the arch

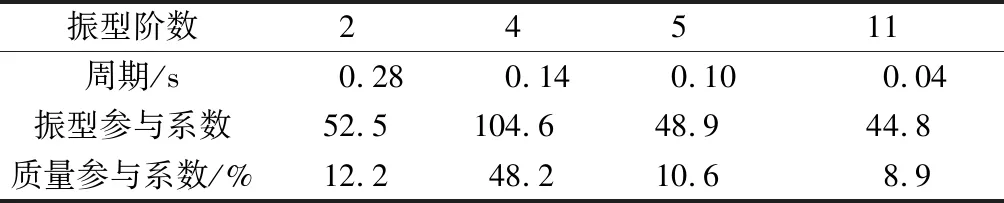
振型阶数24511周期/s0.280.140.100.04振型参与系数52.5104.648.944.8质量参与系数/%12.248.210.68.9

2.2 ESDOF体系

为兼顾IMPA方法的准确性和简洁性，本算例选取前两阶竖向主振型进行模态推覆分析.依据振型参数得到荷载的空间分布模式，对格构拱结构进行静力非线性推覆分析，得到各ESDOF体系每一荷载步的特征刚度k*、等效荷载增量ΔF和振型位移增量ΔD，进而可得各ESDOF体系的A-D曲线.图3给出了各ESDOF体系的A-D曲线和k*-D曲线.

a 2阶振型

b 4阶振型

c 5阶振型

d 11阶振型图2 格构拱结构竖向主振型

Fig.2Fundamentalverticalvibrationmodesofthelatticedarch

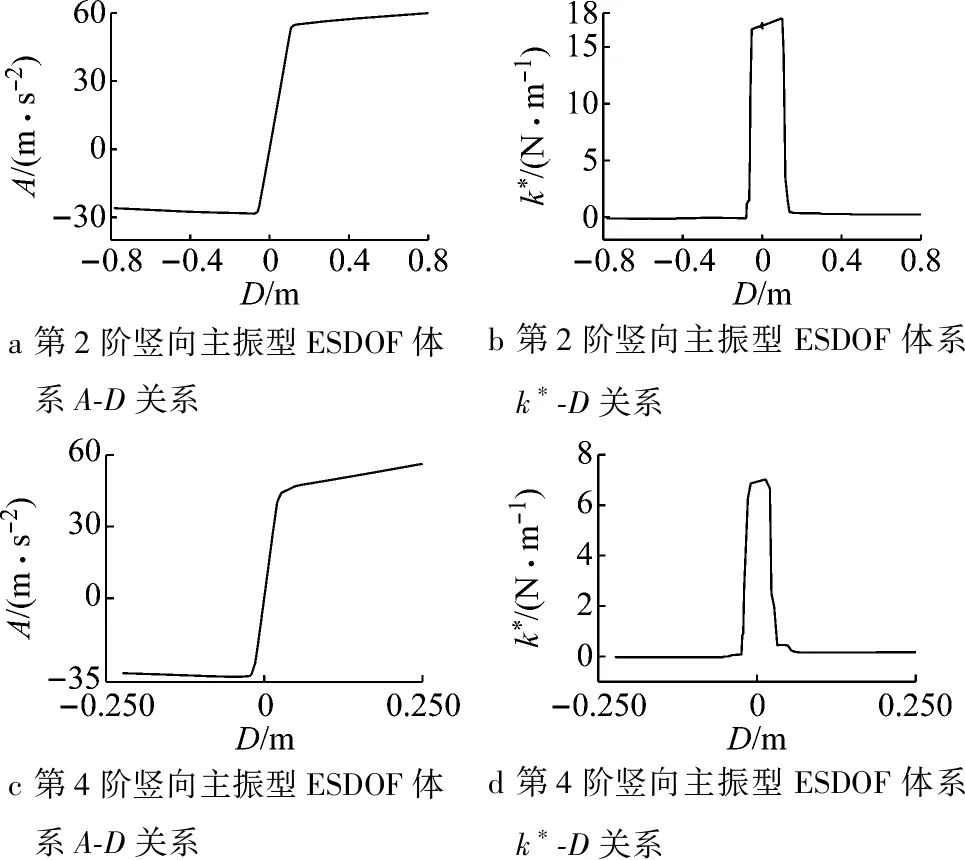
a 第2阶竖向主振型ESDOF体系A-D关系b 第2阶竖向主振型ESDOF体系k∗-D关系c 第4阶竖向主振型ESDOF体系A-D关系d 第4阶竖向主振型ESDOF体系k∗-D关系

图3前两阶竖向主振型A-D和k*-D关系曲线

Fig.3A-Dandk*-DcurvesforthemodalESDOFs

2.3 结构动力响应

2.3.1地震动输入

结构地震反应分析选用日本地球科学与防灾技术研究所(NIED)的K-NET、KiK-net强震数据库中硬土和软土场地各12条地震波的竖向分量作为地震动输入，其伪加速度反应谱见图4.为保证结构在地震作用下进入弹塑性状态，本算例将全部24条地震波的峰值加速度调幅至2.0 g.

2.3.2节点位移响应

采用IMPA方法和RHA方法计算，得到格构拱结构的节点位移响应如图5所示.由图可见，与水平地震动输入时格构拱结构的动力响应由第一阶水平主振型主导[11]不同的是，部分竖向地震动输入(如地震波spectrum-FS3、spectrum-SS5等)时，格构拱结构的节点位移响应由第二阶竖向主振型主导，故而只考虑第一阶竖向主振型显然低估了结构的地震响应.计算结果表明，采用IMPA方法计算得到的目标性能点处的结构位移响应与RHA方法计算结果比较接近且具有以下特征：两者计算结果的位移值随节点号的分布规律和变化趋势基本相同，表明两者在目标性能点处的结构整体变形模式基本一致；与RHA方法的计算结果相比，IMPA方法在X方向最大位移节点处位移计算值的平均误差为16.6%，Z方向最大位移节点处位移计算值的平均误差为10.5%，绝大部分节点误差在30%以内，表明IMPA方法的计算精度满足工程要求.

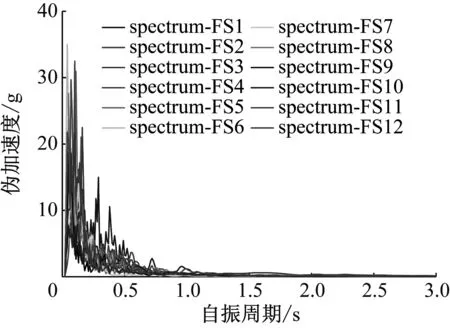
a 硬土场地

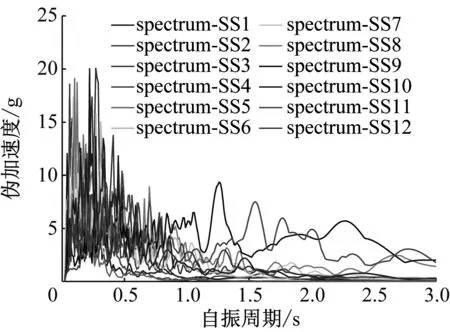
b 软土场地图4 地震波伪加速度反应谱Fig.4 Pseudo acceleration response spectra of the selected seismic waves

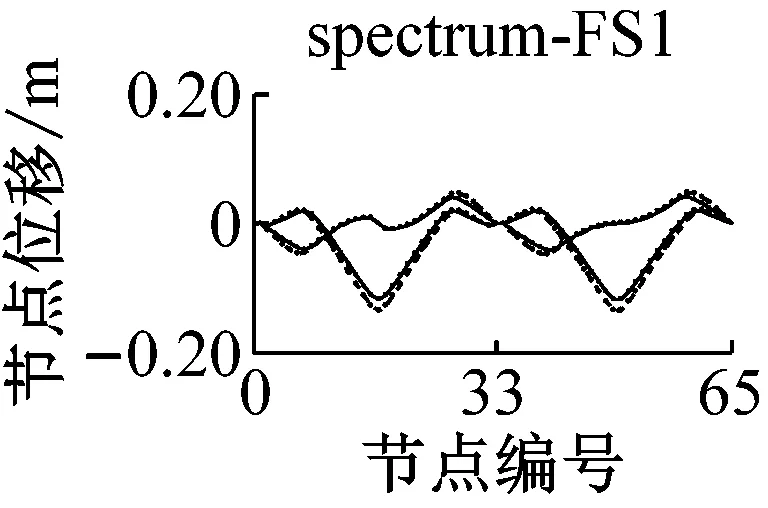
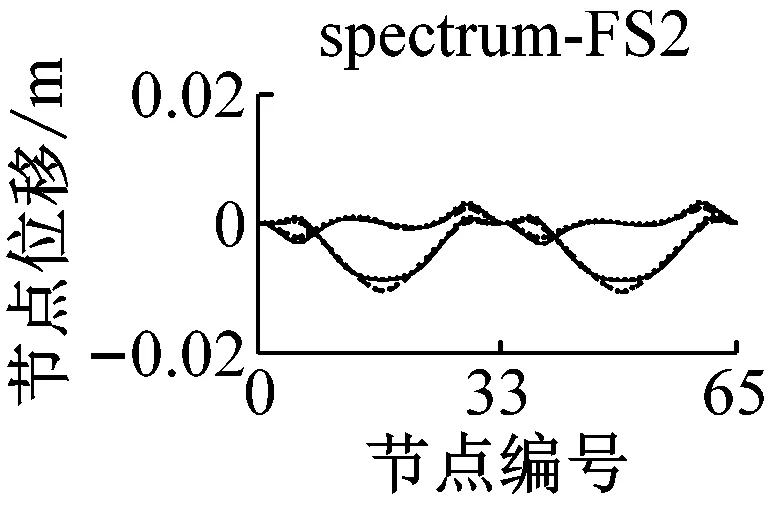
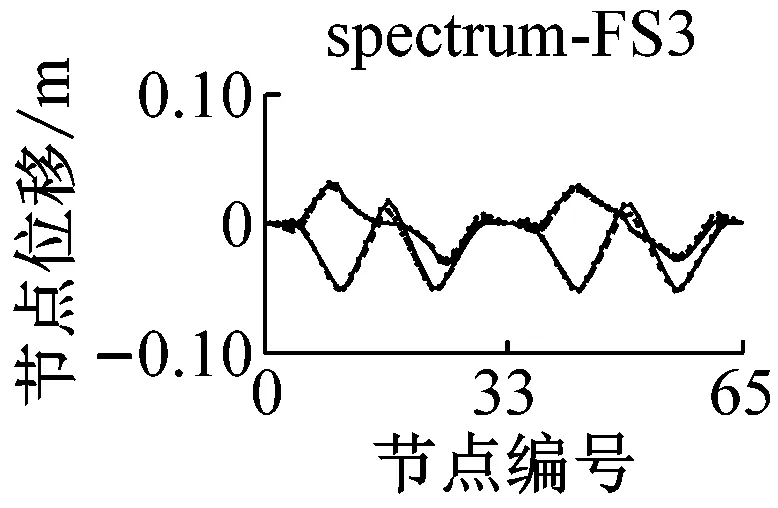
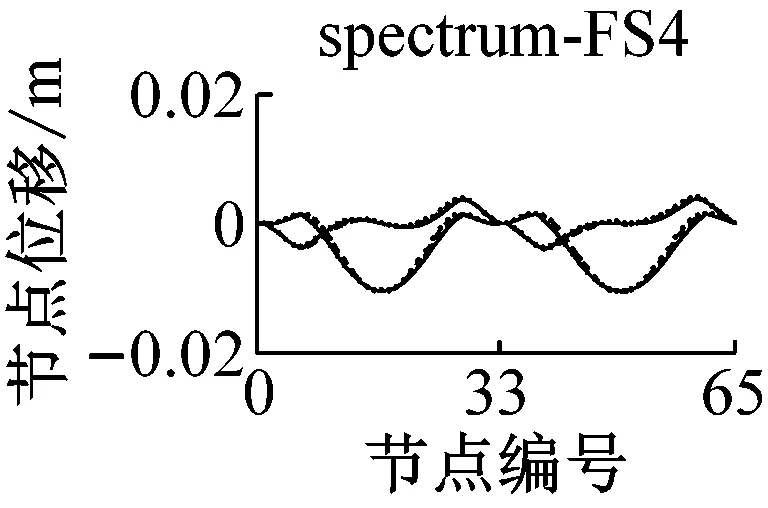
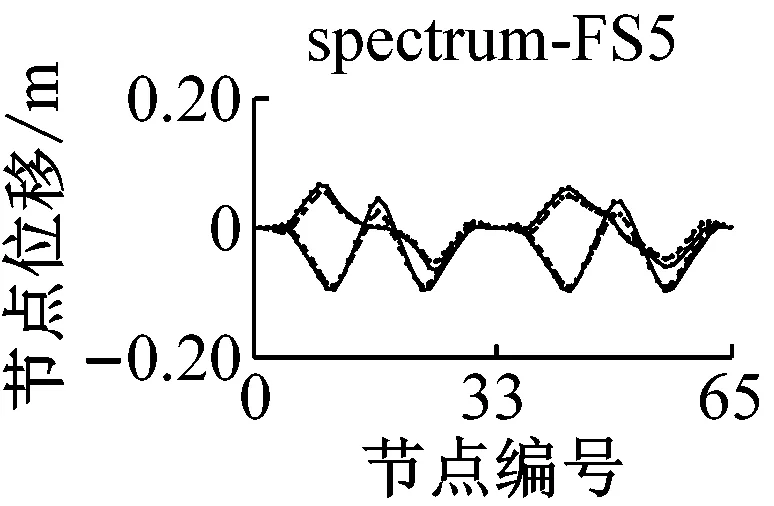
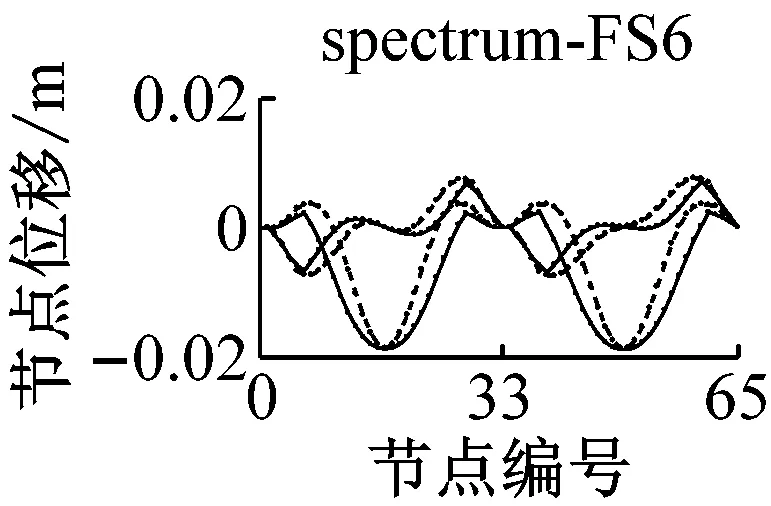
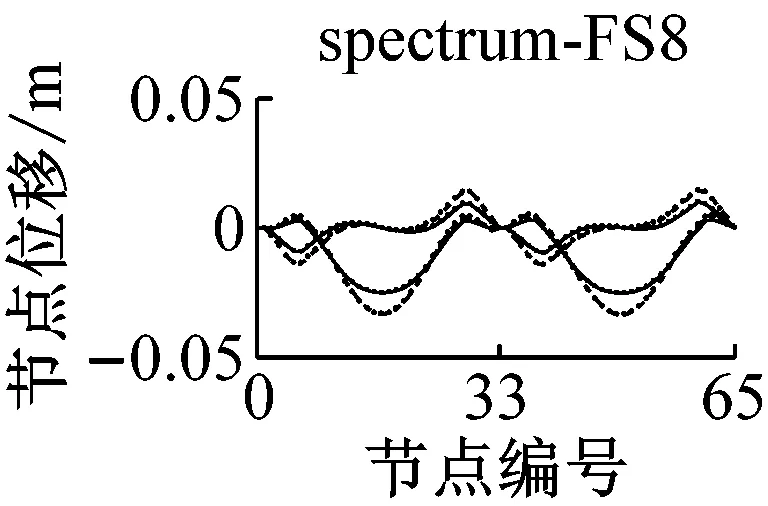
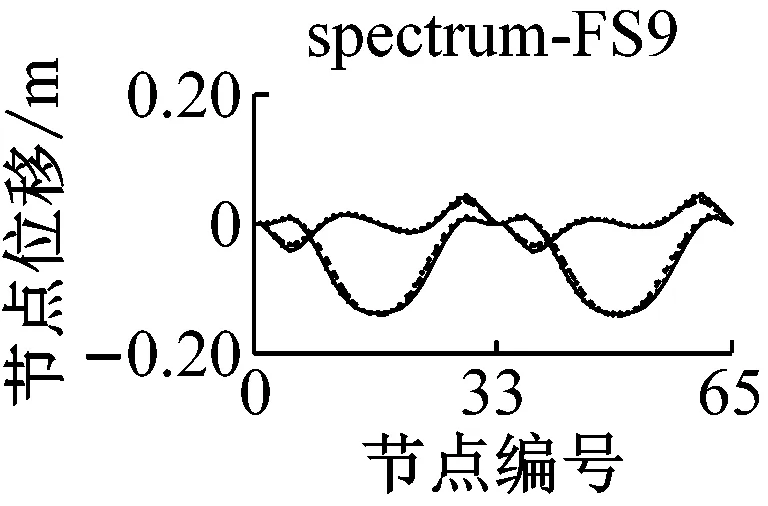
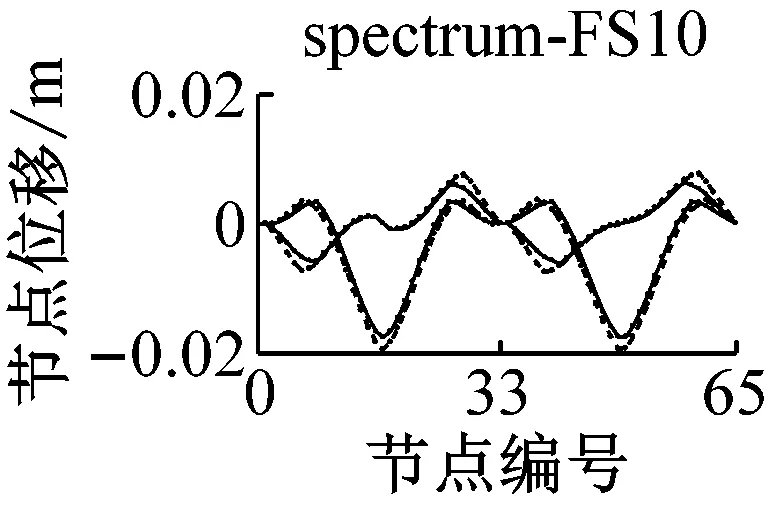
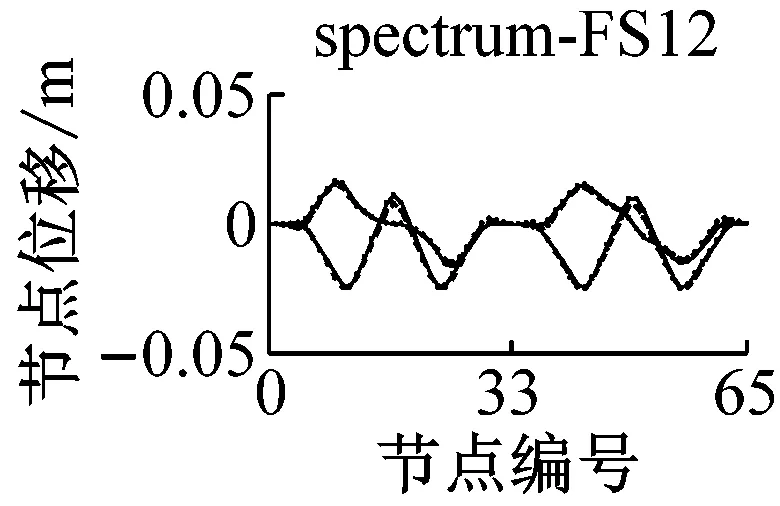
a 硬土场地节点位移对比

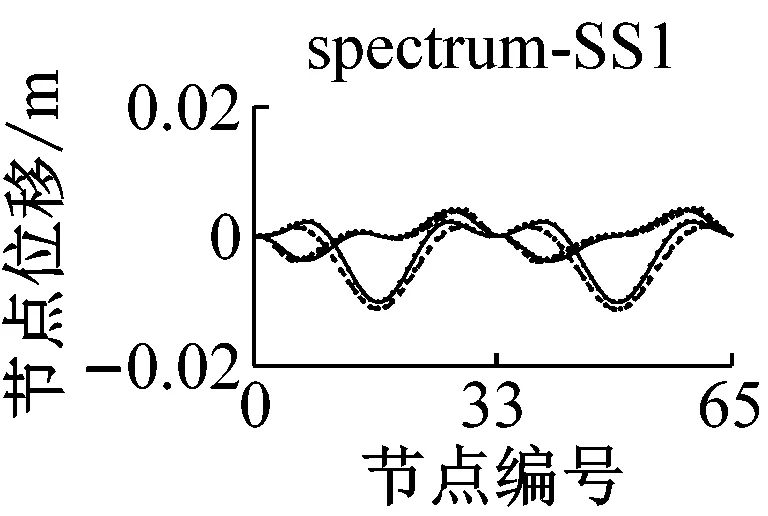
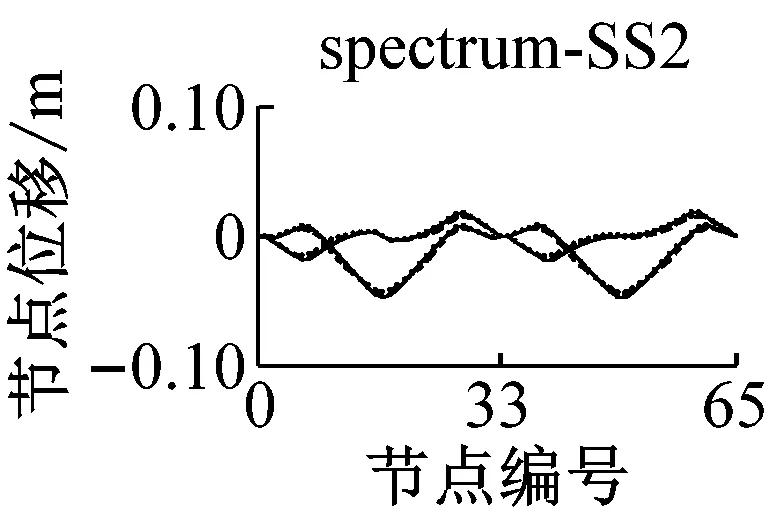
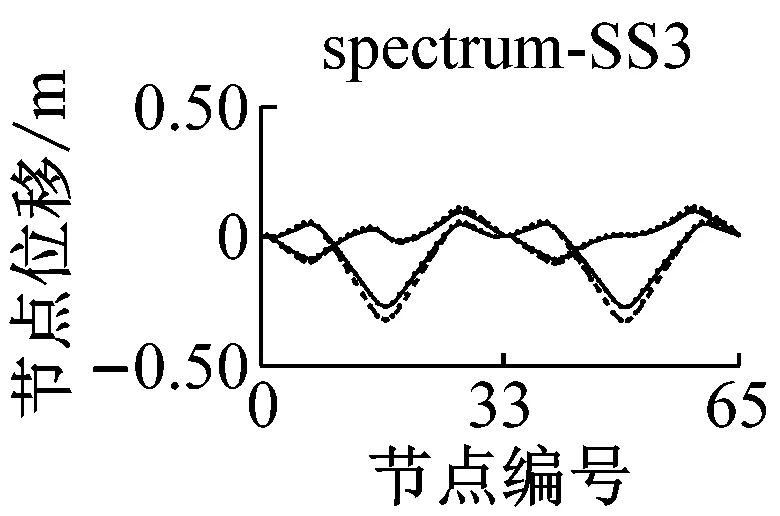
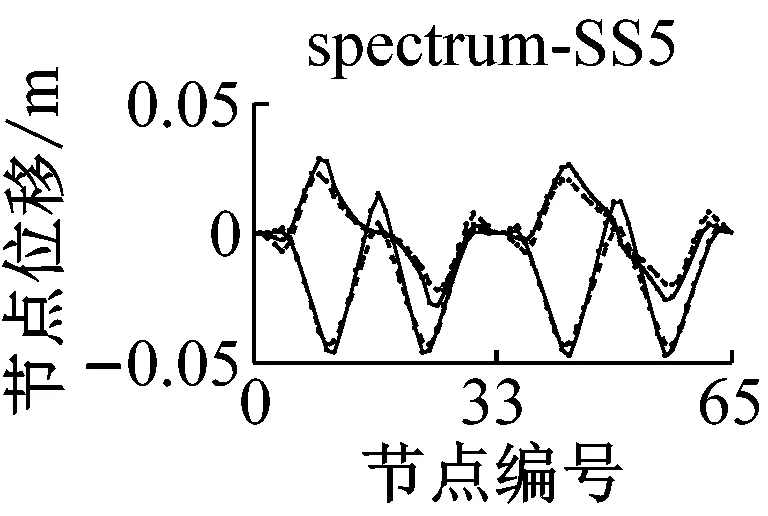
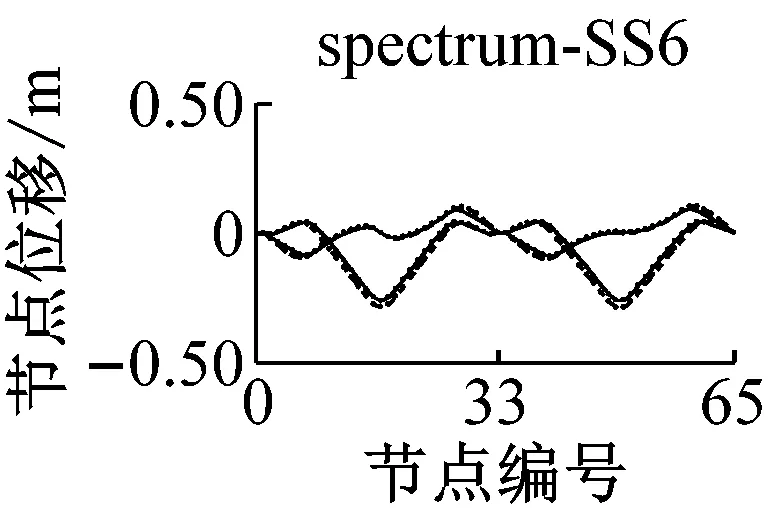
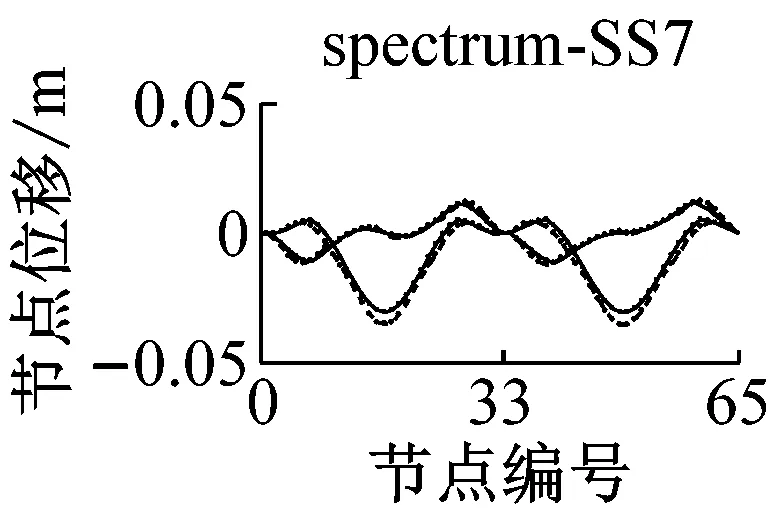
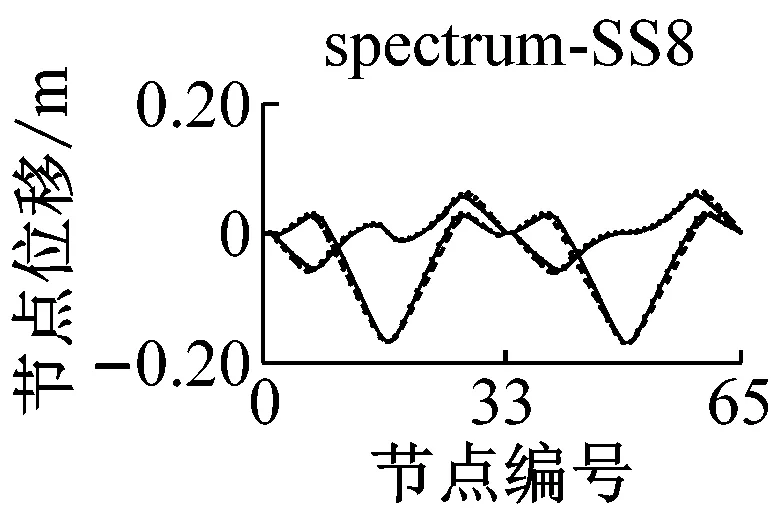
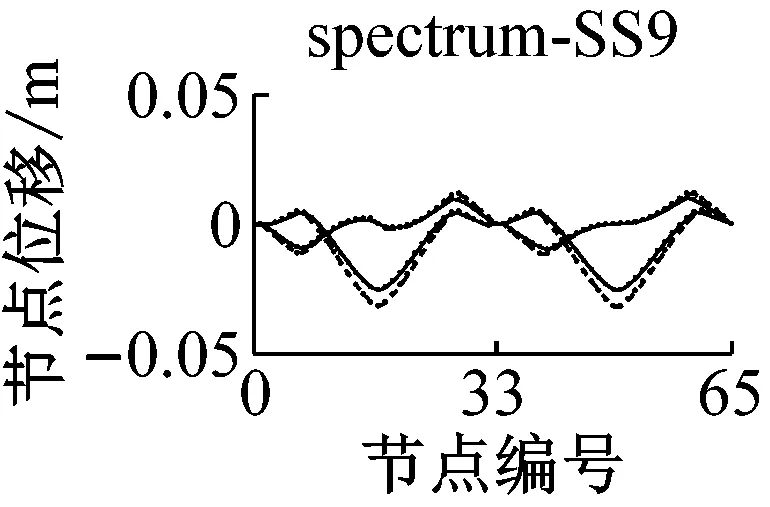
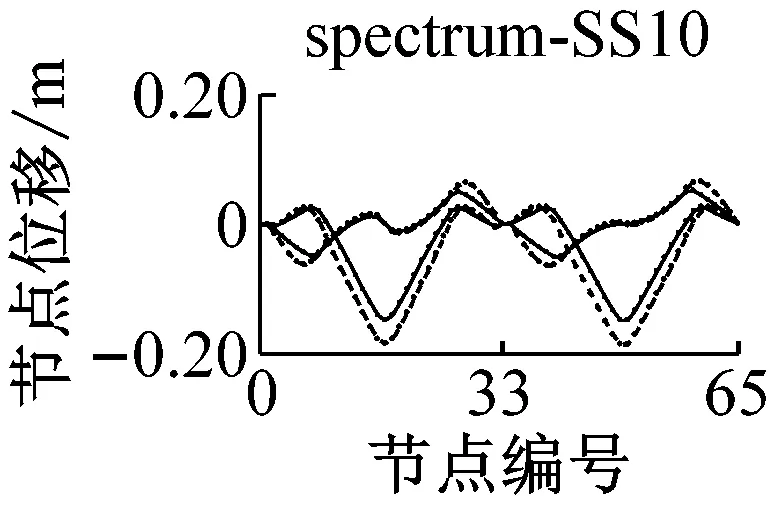
b 软土场地节点位移对比图5 IMPA方法和RHA方法节点位移计算结果对比Fig.5 Nodal displacement responses given by IMPA and RHA

2.3.3单元最不利应力响应

图6a为采用IMPA(图6a)和RHA(图6b)计算得到的单元最不利应力云图.由图可见，两种方法计算得到单元最不利应力结果比较接近且具有以下特征：两者应力分布和变化趋势基本相同，表明两者在性能点处的单元应力状态基本一致；对比RHA方法结果，IMPA方法单元最不利应力计算值平均误差为33.2%，大部分单元误差在35%以内.

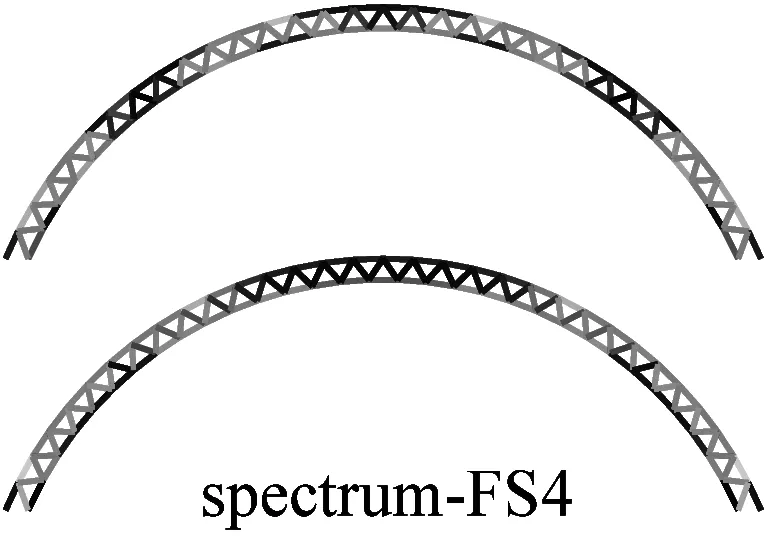
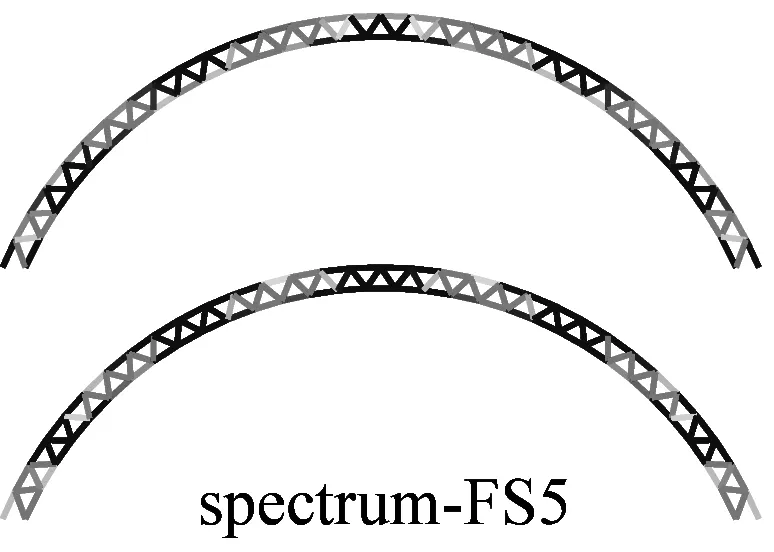
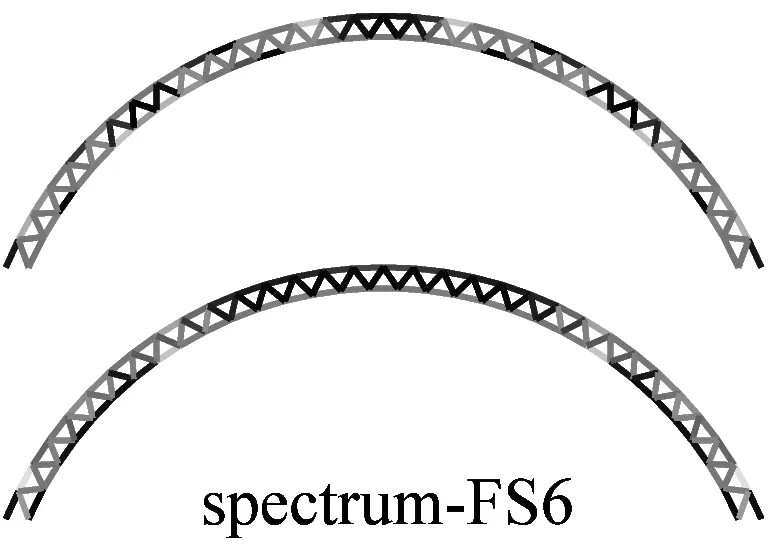
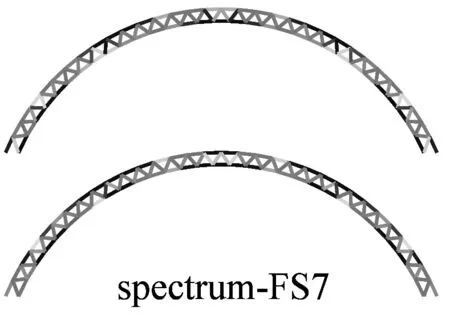
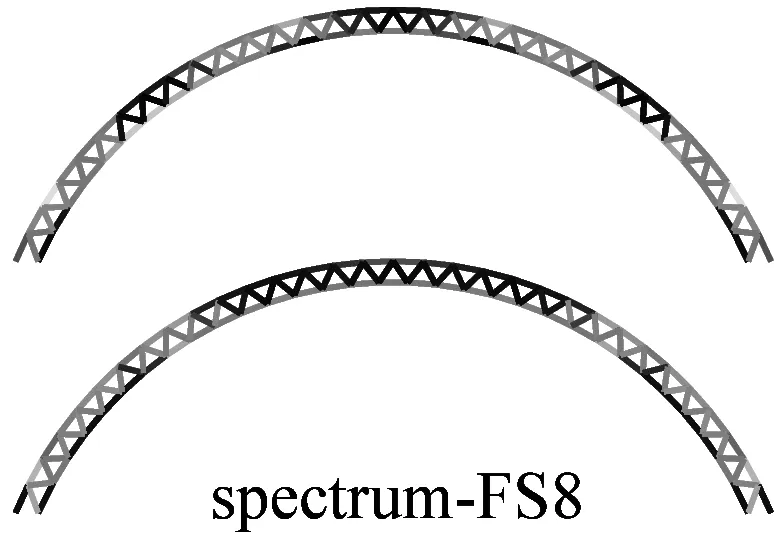
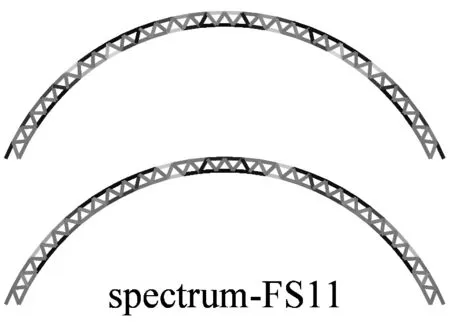
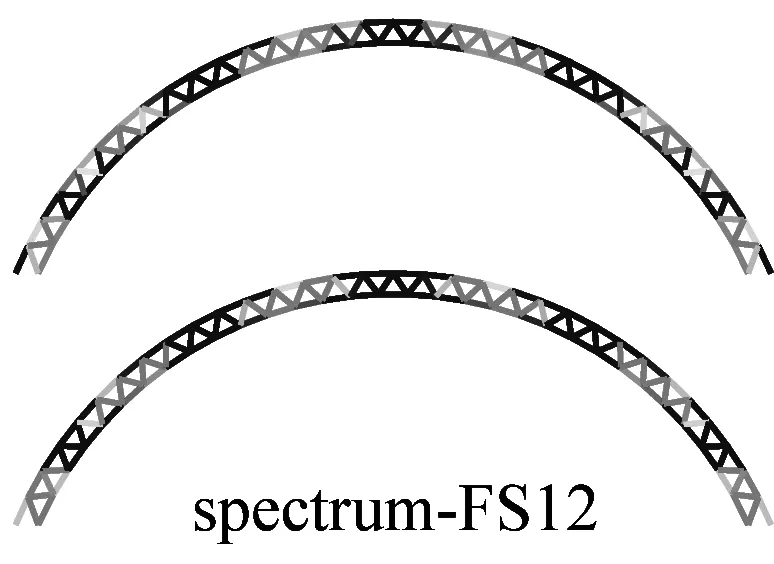
a 硬土场地单元最不利应力云图对比

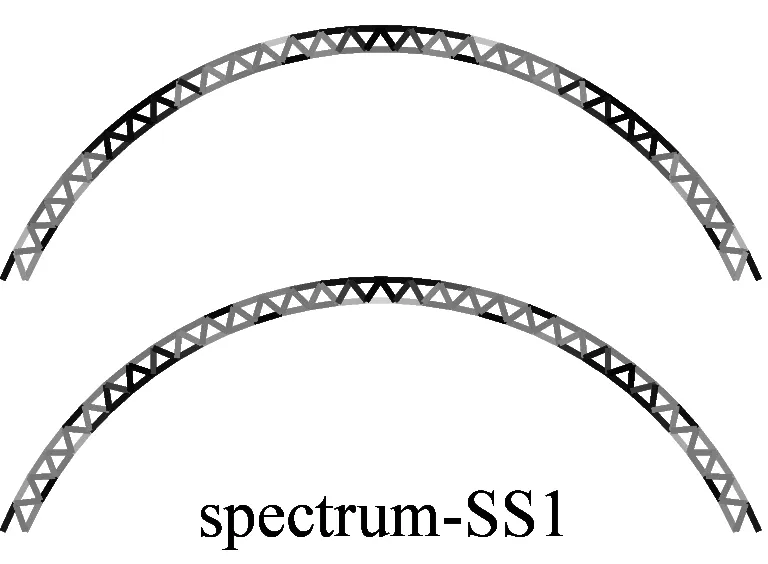
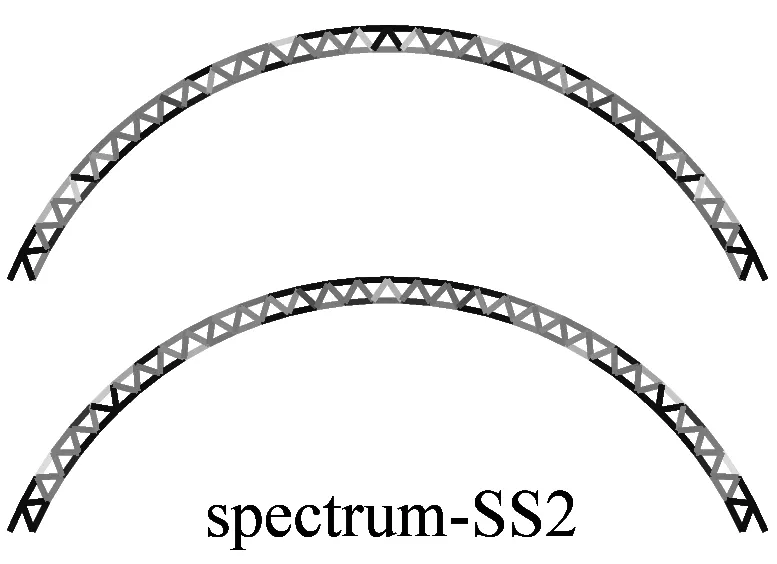
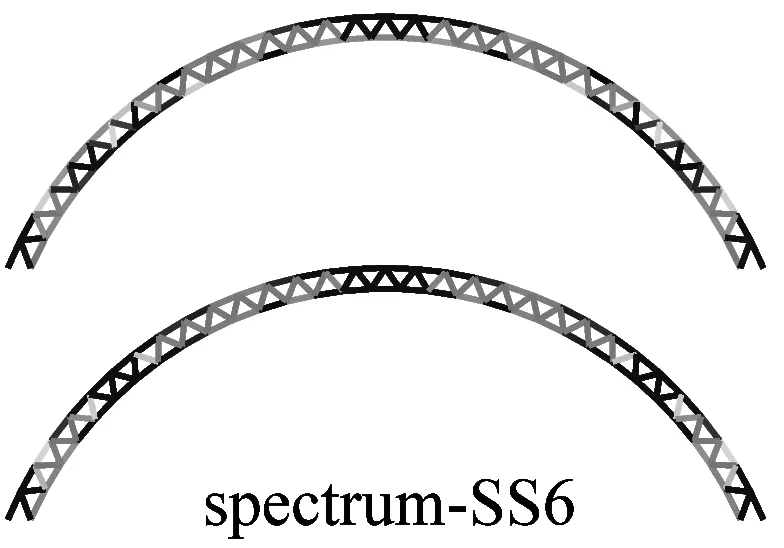
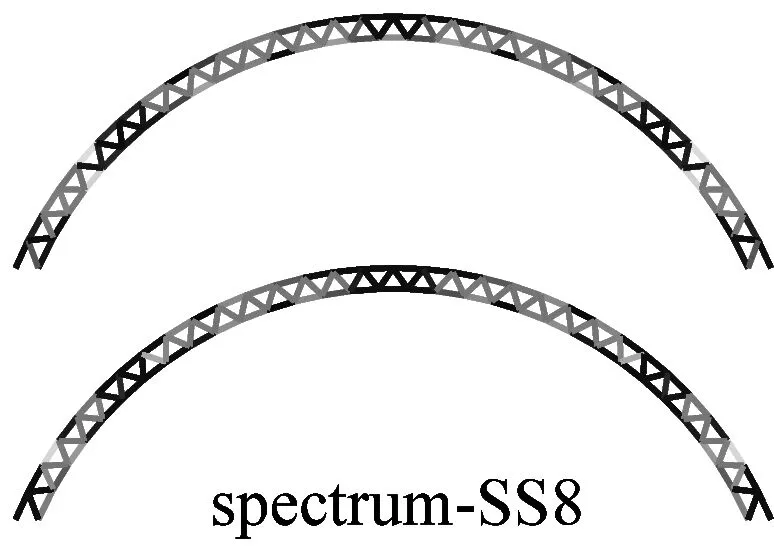
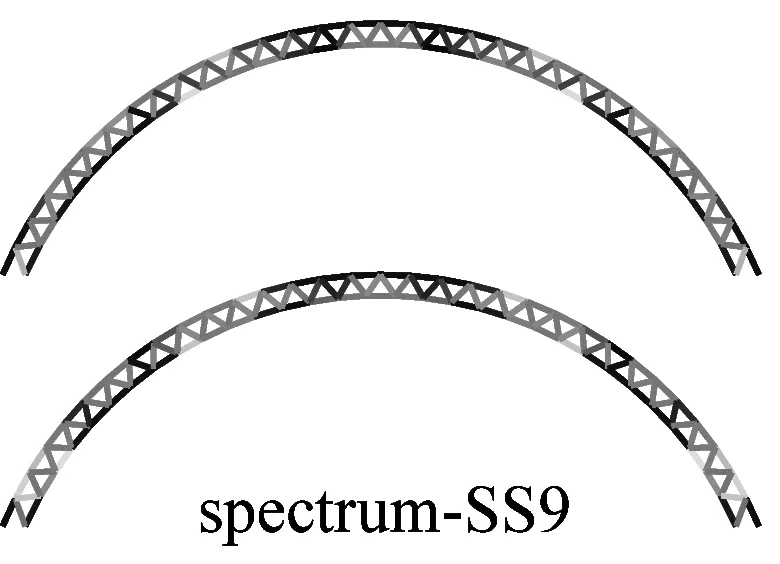
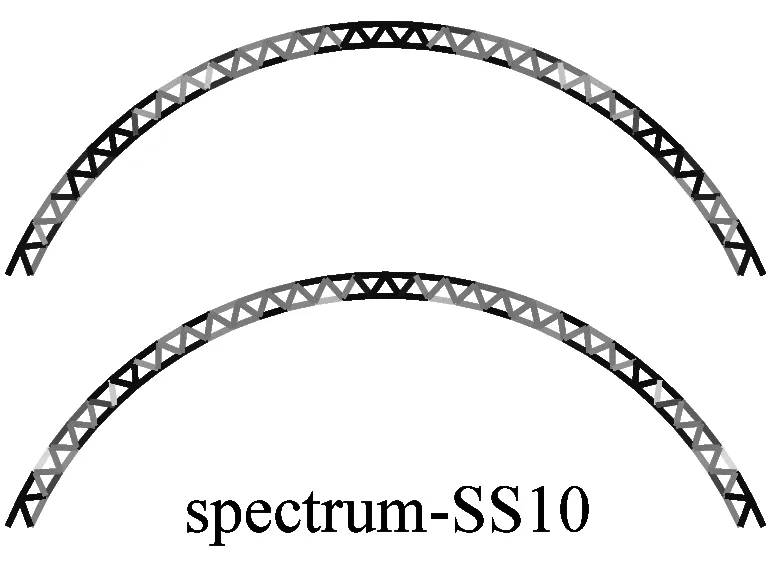
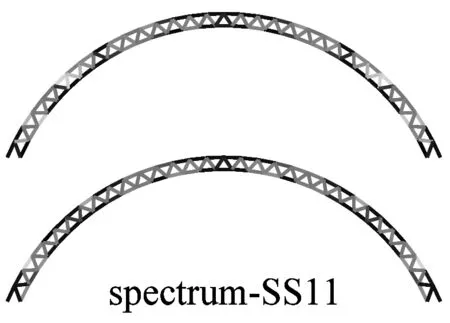
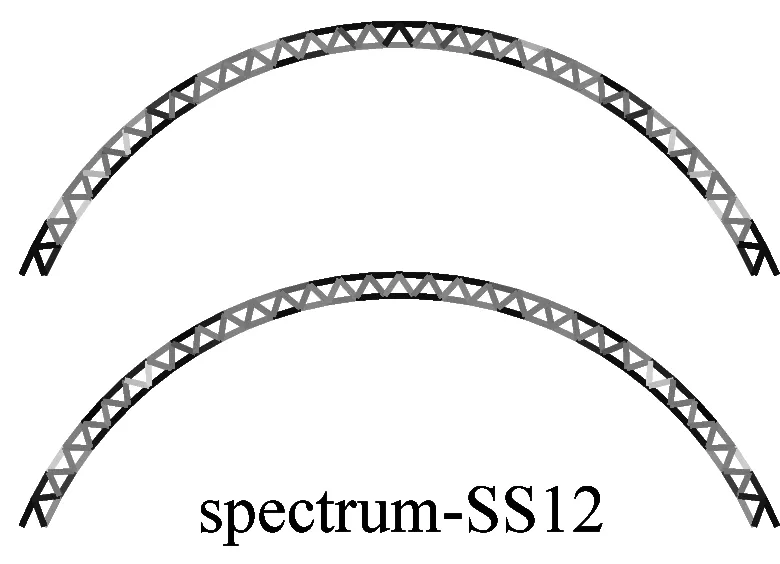
b 软土场地单元最不利应力云图对比图6 IMPA方法和RHA方法单元最不利应力计算结果对比Fig.6 The most unfavorable stresses of elements given by IMPA and RHA

2.4 振型截取阶数的精度影响

针对所选取的24条地震波，分别截取前一、二、三、四阶竖向主振型进行算例模型IMPA分析，并与RHA方法对比，其竖向最大节点位移计算值的相对误差平均值取绝对值见表2.由表可见，随着振型截取阶数的增加，节点位移随节点号的变化趋势与RHA计算结果的一致性有所提高，并且计算精度也有所提高.需要指出的是，部分竖向地震动输入(如spectrum-FS3、spectrum-SS5等)采用第一阶振型进行IMPA分析，由于结构位移响应由第二阶竖向主振型主导，导致误差会超过30%，因此，采用一阶IMPA方法可能会严重低估格构拱结构的竖向位移响应.限于篇幅，结构单元最不利应力响应计算精度对比不再赘述.

2.5 计算耗时对比

与对格构拱结构直接进行RHA分析相比，截取不同阶主振型进行IMPA分析的计算耗时占比列于表3.综合表2和表3可见，在保证精计算精度的前提下，IMPA方法计算耗时比RHA明显减少；随着振型截取阶数的增加，IMPA方法计算耗时也逐渐增加，但相比RHA方法仍然优势显著.

表2 不同阶IMPA与RHA计算精度对比Tab.2 Comparison of computation precision by IMPAs and RHA

表3 不同阶IMPA与RHA计算耗时对比Tab.3 Comparison of computation consumption by IMPAs and RHA

3 结论

基于特征刚度的概念，提出适用于评估大跨度格构拱结构在竖向地震作用下动力响应分析的改进模态推覆分析(IMPA)法，并给出了IMPA方法的理论公式和计算步骤，通过两种场地条件下的数值算例与RHA方法进行对比分析，得到以下结论：

(1) 提出的IMPA方法克服了传统模态推覆分析方法对能力谱的推导依赖于选取某个特征节点的缺点，便于建立能够反映结构整体刚度的等效单自由度体系，并推导出第二阶段推覆荷载公式，通过对结构进行两阶段推覆分析，避免了SRSS组合方式带来的方法误差；

(2) 研究表明，无论硬土还是软土场地，采用IMPA方法计算竖向地震作用下大跨度格构拱结构的动力响应具有较好的适用性，节点两方向位移平均误差为16.6%和10.5%，单元最不利应力平均误差为33.2%，计算精度较高；

(3) 理论推导和算例分析都表明，随着竖向振型截取阶数的增加，IMPA方法的计算精度将进一步提高，但计算效率有所下降；

(4) IMPA方法对于大跨度格构拱结构的动力响应分析具有普适性，可推广至水平地震作用下的结构响应评估，且该方法概念清晰，便于程序化.