高墩大跨T 构连续梁延性抗震设计
刘亚宾
(中国铁路设计集团有限公司,天津 300308)
在山区高速铁路的修建过程中,在跨越V 形山谷时常采用T 构连续梁的桥式。 这类梁型的特点是桥墩高、跨度大,地震破坏后修复难度大。 对于T 构桥的抗震设计,国内学者结合工程实例进行了相关研究[1-4]。 吴游宇等对T 构动力有限元分析建模方法进行了研究[5];赖永星等分析了弹性状态下T 构桥墩的地震响应,并与静力响应进行了对比[6];饶少臣对大跨T 构在地震作用下的主要力学指标进行了分析,并给出了处理措施[7];杨浩对两跨T 构桥墩形式和墩高的抗震性能进行了探讨[8]。 总体而言,以往研究对于T 构桥地震响应及抗震性能的研究多停留在弹性阶段,对于罕遇地震作用下桥墩进入弹塑性状态以后的抗震性能分析研究较少。
以某高速铁路(85+75) m 预应力混凝土T 构连续梁为例,建立基于分布式纤维铰的弹塑性有限元模型,对罕遇地震作用下全桥非线性时程进行分析,并进行延性抗震计算。
1 工程概况
某高速铁路跨越山谷时采用(85+75) m 预应力混凝土T 构连续梁(如图1 所示),P1 号墩为主墩,P0、P2 为桥台。 主梁为单箱单室、变截面直腹板形式,支点梁高9.5 m,跨中梁高5.0 m,混凝土标号为C55。P1 为矩形空心墩,墩高54 m,壁厚1.6 m,墩顶纵横向尺寸为8.0 m×8.0 m,桥墩纵向为直坡,横向按1 ∶45 放坡,底宽10.4 m。 P0、P2 号桥台基础为12 根φ1.25 m 钻孔桩,P1 桥墩基础为20 根φ2.0 m 钻孔桩。
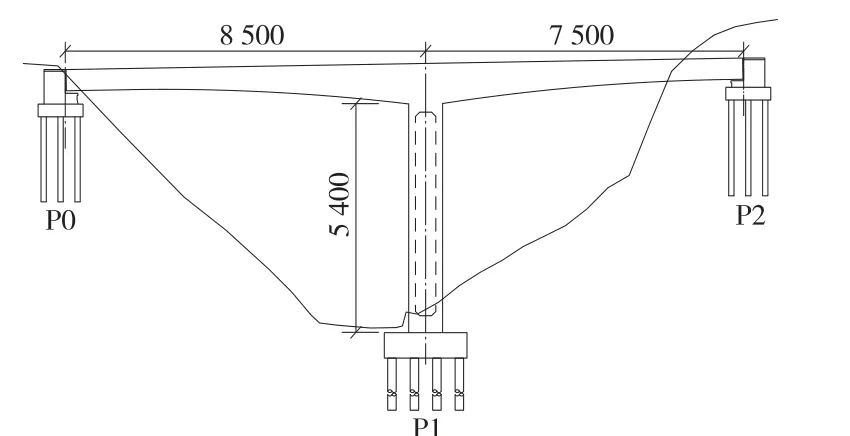
图1 桥梁立面布置(单位:cm)
2 有限元计算模型
采用Midas/Civil 软件建立三维空间有限元计算模型,如图2 所示。 采用梁单元模拟主梁、桥墩、承台,采用节点弹性支承模拟基础的桩土相互作用,P1 桥墩墩顶与主梁为刚臂连接,采用弹性连接单元模拟支座,释放纵桥向自由度,约束横桥向自由度。

图2 有限元计算模型
2.1 塑性铰长度
参考《公路桥梁抗震设计细则》[9],等效塑性铰长度取式(1)和式(2)计算结果的较小值,有
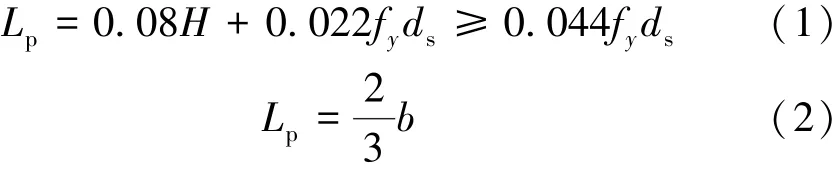
式中:H——悬臂墩高度或塑性铰截面到反弯点距离;
b——矩形截面短边尺寸或圆形截面直径;
fy——纵向钢筋抗拉强度标准值/MPa;
ds——纵向钢筋直径。
本桥桥墩墩高H=54 m,截面短边尺寸b=8 m,纵向钢筋抗拉强度标准值fy=500 MPa,纵向钢筋直径ds=32 mm。 纵向地震作用下,墩顶和墩底均为塑性铰区[10],反弯点距墩顶18 m,距墩底36 m,计算可得墩顶等效塑性铰长度Lp=1.79 m,墩底等效塑性铰长度Lp=3.23 m。 横向地震作用下,墩底为塑性铰区,计算可得等效塑性铰长度Lp=4.67 m。 在进行地震反应分析时,等效塑性铰长度范围内被赋予非弹性铰特性。
2.2 本构关系
采用分布式纤维铰模型模拟非弹性铰,将图3 所示桥墩截面分割为若干纤维块,并按照钢筋、约束混凝土和保护层混凝土分别指定材料特性[11-13]。 其中,采用双线性模型模拟钢筋本构关系,其应力应变曲线如图4 所示;采用Mander 模型模拟混凝土本构关系[14],其应力应变曲线如图5 所示。

图3 桥墩截面配筋(单位:cm)
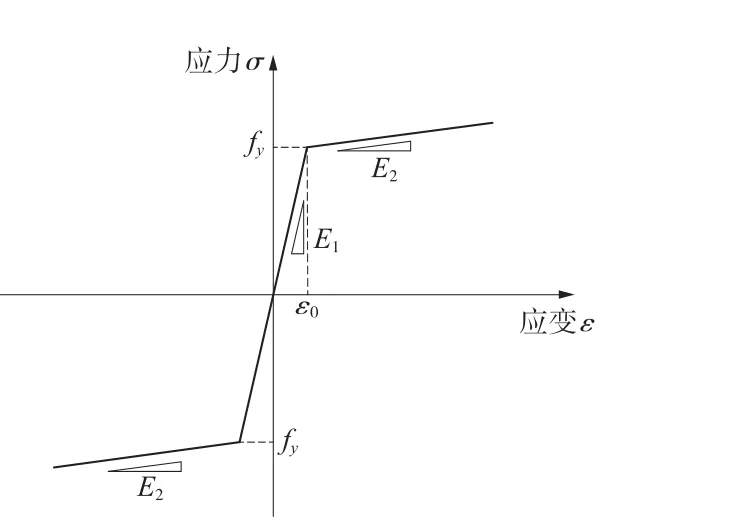
图4 钢筋本构关系
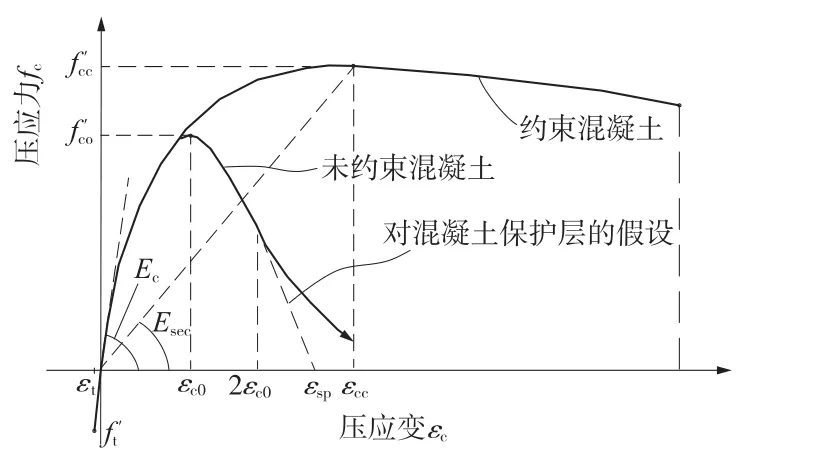
图5 混凝土本构关系
约束混凝土的压应力计算公式为
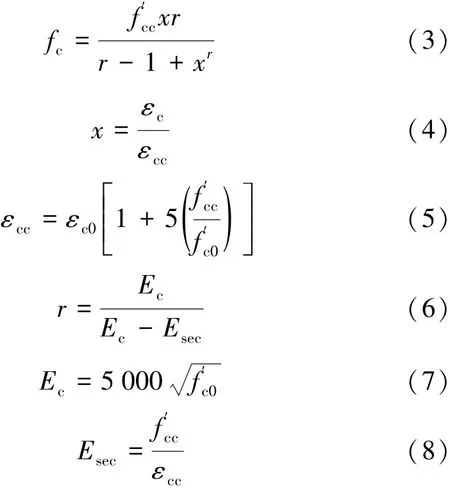
式中 fc——混凝土压应力;
εc——混凝土压应变;
3 地震动输入
根据该项目《工程场地地震安全性评价报告》,罕遇地震下地震动峰值加速度为0.435g,特征周期为0.6 s,对应的三条地震动加速度时程曲线如图6 所示。对于本桥,在进行地震反应分析时,分别采用“纵向+竖向地震输入”、“横向+竖向地震输入”两种作用方式,其中竖向地震加速度取水平向地震加速度的0.65 倍[15]。
4 计算结果分析
4.1 动力特性
采用Lanczos 法进行结构动力特性分析,本桥前5 阶振型周期及振型描述见表1。

表1 结构动力特性

图6 地震动加速度时程曲线
4.2 非线性时程分析结果
在“纵向+竖向”地震作用下,桥墩墩顶和墩底弯矩时程曲线以及对应的截面屈服弯矩如图7、图8 所示,桥墩墩顶纵向位移时程曲线如图9 所示。 由图7、图8 可以看出,在三条地震波输入的情况下,桥墩墩底和墩顶截面均达到屈服状态,需要进行延性验算。
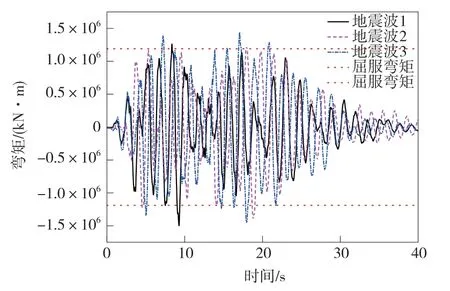
图7 桥墩墩底弯矩时程曲线(纵+竖)

图8 桥墩墩顶弯矩时程曲线(纵+竖)
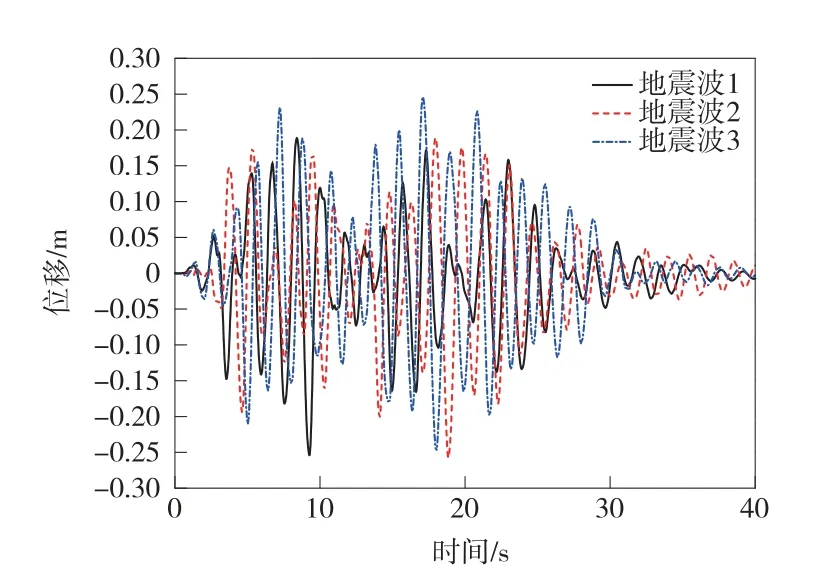
图9 桥墩墩顶纵向位移时程(纵+竖)
在“横向+竖向”地震作用下,桥墩墩底弯矩时程曲线以及对应的截面屈服弯矩如图10 所示,桥墩墩顶横向位移时程曲线如图11 所示。 由图10 可以看出,在三条地震波输入的情况下,桥墩墩底截面均达到屈服,需要进行延性验算。
4.3 桥墩延性抗震验算
(1)位移延性比验算
根据《铁路工程抗震设计规范》[15],钢筋混凝土桥墩延性验算应满足式(9)的要求,有
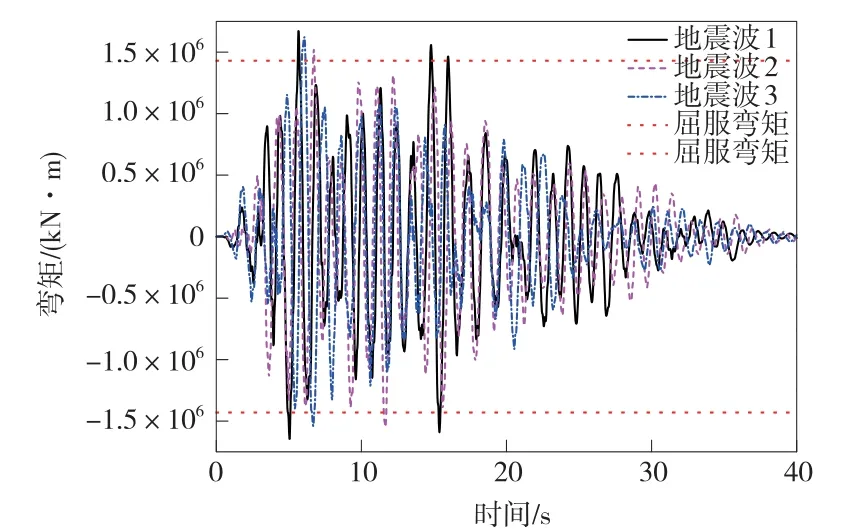
图10 桥墩墩底弯矩时程曲线(横+竖)
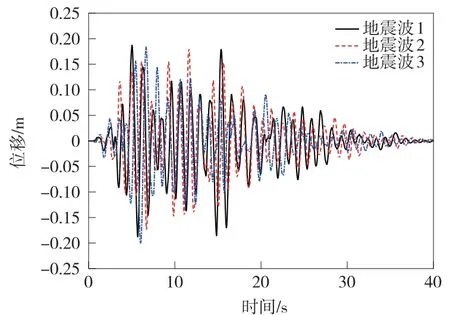
图11 桥墩墩顶横向位移时程(横+竖)
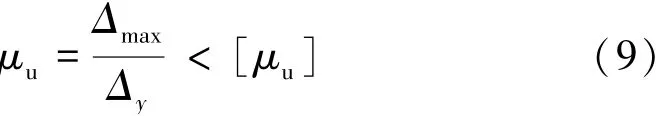
式中 μu——非线性位移延性比;
[μu]——允许位移延性比,取4.8;
Δmax——桥墩非线性响应最大位移;
Δy——桥墩屈服位移。
在“纵向+竖向”地震作用下,3 条波对应的桥墩屈服位移与非线性响应的最大位移见表2。 由表2 可知,桥墩最大非线性位移延性比为1.42,满足规范要求。

表2 桥墩非线性位移延性比(纵向+竖向地震) cm
在“横向+竖向”地震作用下,3 条波对应的桥墩屈服位移与非线性响应的最大位移见表3。 由表3 可知,桥墩最大非线性位移延性比为1.16,满足规范要求。

表3 桥墩非线性位移延性比(横向+竖向地震) cm
(2)桥墩抗剪验算
在“纵向+竖向”和“纵向+横向”地震作用下,桥墩塑性铰区域抗剪能力验算结果见表4。 由表4 可知,桥墩墩顶和墩底塑性铰区域抗剪能力均满足要求。

表4 桥墩抗剪验算结果 kN
4.4 支座验算
“纵向+竖向”地震作用下,支座的最大位移为26.3 cm。 为防止主梁与桥台发生碰撞,主梁梁端与桥台间的缝隙宽度需大于地震位移。
“横向+竖向”地震作用下,支座抗剪能力验算结果见表5。 由表5 可知,罕遇地震下支座横向抗剪能力不足。 因此,本桥在支座内侧设置了横向限位装置,与支座共同承担横向剪力,防止支座被剪断。

表5 支座横向抗剪验算结果 kN
4.5 基础验算
本桥主墩基础采用了20 根φ2 m 钻孔灌注桩,混凝土标号为C40,纵筋型号为HRB500,截面配筋率为2.4%。 将地震作用下墩底内力反算为单桩内力,取最不利受力单桩进行验算,结果见表6。 由表6 可知,在“纵向+竖向”和“横向+竖向”地震作用下,桩基础强度满足要求。

表6 基础最不利单桩验算结果 kN·m
5 结论
以某高速铁路(85+75) m 预应力混凝土T 构连续梁为例,建立基于分布式纤维铰的弹塑性有限元模型,采用非线性时程分析方法,对全桥进行地震反应分析与延性抗震计算,得到以下结论。
(1)采用基于分布式纤维铰的弹塑性模型进行T构延性抗震设计可行,可以有效模拟桥墩塑性铰区的非线性特性。
(2)在罕遇地震作用下,地震沿“纵向+竖向”输入时,桥墩墩底和墩顶截面均达到屈服,进入塑性状态;地震沿“横向+竖向”输入时,桥墩墩底截面达到屈服,进入塑性状态。
(3)“纵向+竖向”和“横向+竖向”地震作用下,桥墩在3 条地震波下的最大位移延性比分别为1.43 和1.16,均小于容许值4.8,满足铁路规范要求,桥墩塑性铰区域抗剪能力满足要求。
(4)“纵向+竖向”地震作用下,支座位移较大,桥台与梁端需要设置足够的缝隙,防止主梁与桥台碰撞。“横向+竖向”地震作用下,支座横向抗剪能力不足,需要在支座处设置横向限位装置,防止支座被剪断。
(5)“纵向+竖向”和“横向+竖向”地震作用下,桩基础强度均满足要求。

