GNSS 非差非组合精密单点定位应用研究

孙忠吉

(中国铁路设计集团有限公司，天津 300251)

随着全球导航卫星系统(Global Navigation Satellite System，GNSS)的快速发展以及卫星产品精度的改 善， 多 系 统 精 密 单 点 定 位( Precise Point Positioning，PPP)已成为当前研究和应用的热点[1-5]。相较于双差GNSS 观测，PPP 具有无需地面基准站、单机作业、定位不受作业距离的限制、作业机动灵活、成本低等诸多优势，并且可直接获取测站在国际地球参考框架(International Terrestrial Reference Frame，ITRF)下的高精度位置坐标。 在多导航系统(GPS、GLONASS、Galileo 和BDS)观测条件下，非差非组合 PPP 处理多频数据更为灵活，不仅可以避免观测量组合引起的噪声放大[6]，而且在定位精度和收敛速度方面较传统的PPP 均有较大的改善。 非组合 PPP 能提供准确的电离层信息，可作为研究电离层的一种新手段。

近年来，非组合PPP 的研究得到了迅速发展。 章红平[7]、张宝成[8]和Lou 等[1]阐释了非差非组合PPP的理论方法，分析了接收机伪距硬件延迟偏差和先验电离层精度对其收敛速度的影响;闫伟等[6]讨论了非组合精密单点定位算法精密授时的可行性，结果表明，在同等条件下，非组合PPP 算法授时精度优于传统PPP 算法，可以用于精密授时解算;张辉等[5]提出了一种电离层约束权因子搜索算法，使得PPP 静态定位的平均收敛时间有了明显的减少;最近，Zhou F 等[9]研究了GLONASS 码频间偏差对PPP 的影响，并公开发表了多系统非差非组合PPP 的计算程序，这将有助于理论-实验研究向实际应用的推广。 上述研究从理论上阐述了非差非组合多系统PPP 的可行性，也讨论了影响定位精度的多种因素，但仍有一些问题需要阐述。 以下将研究:标准精密单点定位(SPPP)和非差非组合定位(GIMPPP)的定位精度和收敛时间。

1 数学模型

传统PPP 算法通过组合观测值来消除电离层延迟一阶项，但残余的电离层延迟项使得观测噪声被放大[10]，而非差非组合PPP 算法不进行观测值间的组合，直接以参数的形式估计卫星斜路径上的电离层延迟，从而在不放大观测值噪声的同时消除电离层误差[11]，其伪距和载波观测方程为

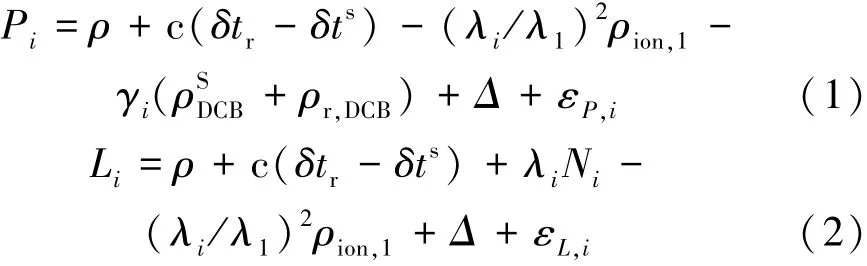
其中，P 和L 表示伪距和载波观测值;ρ 为接收机到卫星之间的几何距离;c 表示光速;s 和r 分别为卫星和接收机;δtr、δts表示接收机和卫星的钟差;γi表示伪距DCB(Differential Code Bias)的系数;为伪距观测值上的卫星和接收机硬件延迟误差;λ 和N 表示载波波长和模糊度;Δ 表示其他误差，包括对流层、天线相位中心偏差等;εL和εP分别为伪距和载波相位观测值的观测噪声。

在观测数据非组合过程中，需要对cm 级及以上的系统误差进行改正，包括接收机及卫星天线相位中心偏差、对流层延迟干分量(SAAS 模型)、固体潮误差改正、海潮误差改正和极潮误差改正等[12]。 本研究采用IGS 发布的精密钟差产品，包括轨道、钟差、相位等，并采用CODE 发布的DCB 文件对码观测方程中与卫星和接收机频率有关的硬件延迟进行修正。 上述数学模型仅提供了基本的观测方程以及误差改正模型和方法，文献[1]给出了更加详细的数学模型及误差处理流程。

2 实验与分析

为了对比研究两种PPP 算法在单卫星导航系统和多卫星导航系统组合时的定位精度及收敛时间，尤其是GIMPPP 在电离层活跃的低纬度地区的定位表现，选取位于中国香港的HKWS 站2017 年200 d 的观测数据来进行实验。 该测站接收的GNSS 数据包括GPS、GLONASS 和BDS，可用于不同导航系统之间的组合。共设计了6 组实验来组合不同的卫星导航系统，并在每组实验中分别对比SPPP 和GIMPPP 在定位精度和收敛时间上的差异。 数据处理策略如表1 所示。

表1 数据处理策略

基于上述数据处理的算法和策略，得到的数据处理结果如图1、图2 和表2 所示。 利用SPPP 算法得到的GPS 和GLONASS 水平向单点定位精度为0.63 ～1.75 cm，垂向精度为2.49～3.14 cm，定位收敛时间保持在30 min 以内;而利用BDS 数据获取的单点定位精度稍差，水平向达3 cm，垂向精度为6 cm，且定位收敛时间(326 min)明显高于GPS 和GLONASS，这与BDS星座的几何分布、卫星轨道精度以及卫星钟差的精度有直接的关系[13]。 多系统组合模式下的SPPP 在定位精度和定位收敛时间上均有提高，水平向精度优于1 cm，垂向精度优于3 cm，且GPS+GLONASS+BD 共同组合的定位精度最好，此时单点定位的收敛时间仅为19.5 min。 上述实验对比结果表明，在SPPP 算法下，相较于单个卫星导航系统，采用多卫星导航系统的组合能够明显提高单点定位精度和收敛时间。

图1 SPPP 算法下的不同卫星系统及其组合的精密单点定位结果

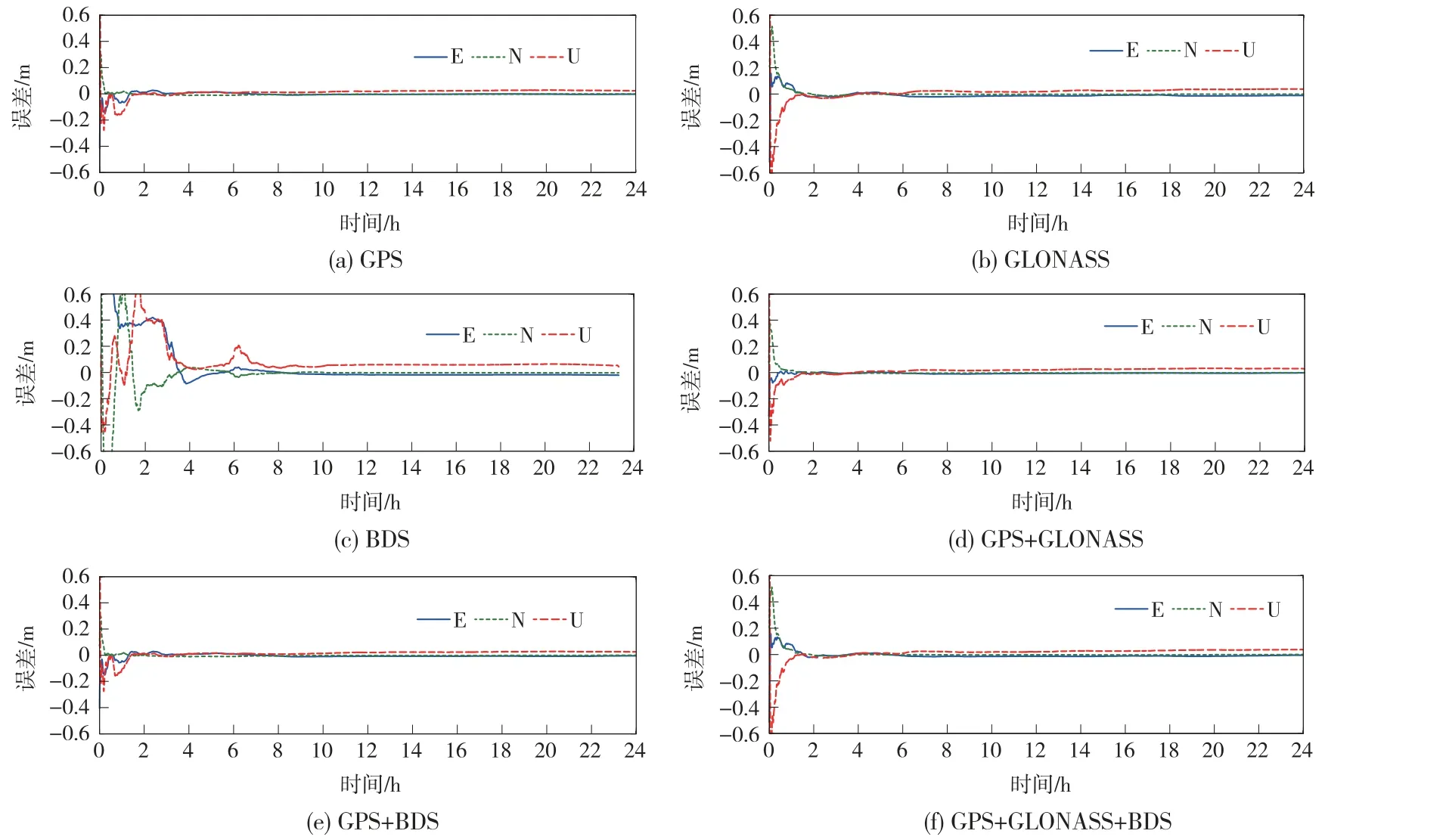
图2 GIMPPP 算法下的不同卫星系统及其组合的精密单点定位结果

对于单个导航系统来说，GIMPPP 算法的定位结果如表2 和图2 所示。

表2 结果对比

对于GPS 和BDS 数据，GIMPPP 得到的定位精度有所提升，收敛时间明显较少，尤其对于BDS 数据，其收敛时间减少了38%。 而对于GLONASS 数据，GIMPPP 算法反而降低了定位精度，增加了收敛时间，这可能与电离层先验改正量和实际观测量的权比配置不合理有关[5]。

相较于单系统GIMPPP，多系统GIMPPP 的结果精度有所提高，水平向定位精度为0.63 ～1.66 cm，收敛时间也显著减少(尤其是GPS+BD 数据)。 值得注意的是，由于电离层先验约束并未对GLONASS 的定位效果有所改善，从而导致GPS+GLONASS、GPS+GLONASS+BD 在GIMPPP 算法下不仅定位精度较SPPP 差，而且在定位收敛时间上也有所增加，这是由于GLONASS 数据的电离层先验改正量和实际观测量的权比配置不合理而引起的[14]。 上述实验表明，GIMPPP 并非总能改善单点定位的精度和收敛时间，该算法的优越性取决于电离层先验改正量和实际观测量的权比是否合适，这也突出了该算法在单点定位方面存在的缺陷(尤其是在电离层活动明显的低纬度地区[15])。 因此，在实际工程应用中应权衡定位误差和收敛时间，选择合适的卫星导航数据以及单点定位算法。 需要说明的是，上述的实验结论是根据一个测站的单天解算结果得来的，仍然缺乏多测站、长时间序列的统计信息，但与本文的主要研究目的并不冲突。

本研究的另一个主要关注点是分析BDS 在PPP方面的表现。 表2 和图3 给出了基于BDS 数据的SPPP 和GIMPPP 的对比结果，可以看出，SPPP 定位精度在水平向和垂直向分别为3 cm 和6 cm，收敛时间长达300 min，这在工程应用中是不现实的，但其定位精度和GPS、GLONASS 相当，能够满足某些工程建设的精度需求。 在加入电离层先验约束后的GIMPPP 算法中，BDS 水平向定位结果有所提高，但垂向精度却变差;定位收敛时间缩短38%，但仍然在200 min 以上。 上述对比表明，加入电离层延迟先验约束的GIMPPP 算法有助于进一步提升BDS 的定位能力，但其定位收敛时间仍然有待提高。 随着全球连续跟踪观测站的持续建设，BDS 卫星轨道以及钟差产品的精度会进一步的提升，这必将改善BDS 的服务能力[16]。

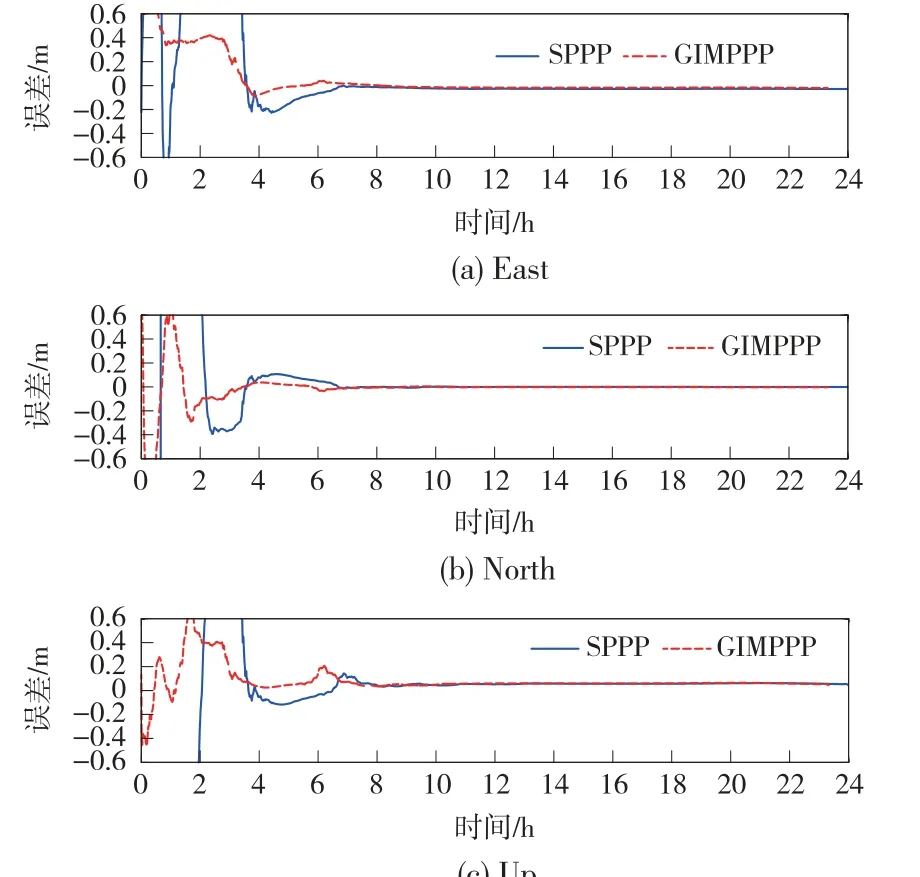
图3 不同算法下的北斗数据精密单点定位结果

3 结束语

阐述了GNSS 非差非组合PPP 的数学模型以及误差处理方法，选取位于中国香港HKWS 观测站的数据，定量对比及分析了SPPP 和GIMPPP 的定位精度和收敛时间。 实验表明:(1)GPS 和GLONASS 单系统SPPP 的定位精度在水平向约为1 cm，垂向约为3 cm;在SPPP 算法下，BDS 数据的水平向精度约为3 cm，垂向精度为6 cm;(2)在多卫星导航系统组合下，SPPP的定位精度有显著改善，在水平向优于1 cm，且定位收敛时间减少;(3) 加入电离层延迟先验约束的GIMPPP 算法能够改善GPS 和BDS 的定位精度和收敛时间，而对于GLONASS 数据却相反;(4)相较于SPPP 算法，GIMPPP 算法缩短了GPS+BDS 的定位收敛时 间， 提 高 了 定 位 精 度， 但 却 延 长 了 GPS +GLONASS+BD 的收敛时间，这与GLONASS 数据的电离层先验改正量和实际观测量的权比配置不合理有关;(5)BDS 数据在SPPP 和GIMPPP 算法下的定位精度和收敛时间均较GPS 和GLONASS 差。 随着BDS 系统的完善，将有助于改善这一差距。