具有脉冲源项的二阶半线性奇摄动边值问题
谢亚南,谢峰
(东华大学理学院,上海201620)
1 引言
奇异摄动理论和方法来源于对天体力学和流体力学边界层理论的研究[1],目前已是解决非线性问题的重要手段之一.奇异摄动问题广泛存在于力学、物理、生物等学科中,这类问题的典型特征是其解通常包含多个时间尺度,如解的边界层现象和内部层现象.至上个世纪九十年代末,二阶奇异摄动两点边值问题获得了充分的研究,光滑的二阶奇摄动边值问题的边界层理论和空间对照理论已较为完善[2−4].
近年来,具有不连续系数和不连续源项的奇异摄动问题受到较多关注[5−8],这类模型经常出现在流固耦合等实际问题中.如文[5]中,Linß Torsten研究了具有集中点源的对流扩散问题

其中δd=δ(x −d)为Dirac-delta函数,这是一类典型的具有不连续系数的奇摄动边值问题.在文[6]中,Gracia 和O’Riordan考虑了一个具有移动脉冲的奇异摄动对流扩散问题,作者构造出解原问题的参数一致的数值方法.
本文研究一类具有典型脉冲源项的二阶半线性奇异摄动边值问题:

其中f(x,y)和g(x)分别为[a,b]×R和[a,b]上的充分光滑函数,0<ε ≪1为摄动参数,A和B为给定常数,I(s) = e−s2为脉冲源项.这类问题可以看做是具有集中点源奇摄动问题的光滑化.令ε →0,其退化问题为

这里方程(1.1)的右端不依赖于未知函数的一阶导数y′(x),故方程(1.1)为二阶半线性微分方程[1].一般而言,它在x=x0处不连续.退化问题的解可看作具有集中点源,因而原问题的解除展示边界层外,可能会出现内部层现象.本文将用合成展开法和微分不等式理论研究问题(1.1)-(1.2)解的存在性和渐近估计.
2.构造形式渐近解
首先作如下假设:
(H)f(x,y)∈C∞([a,b]×R),存在常数ℓ>0,使得

因退化问题的解在x=x0处的非光滑性,原问题的解除了在x=a和x=b处具有边界层性质外,在x=x0处可能具有内部层现象.因此,按照合成展开法,我们寻求问题(1.1)-(1.2)的如下形式渐近解y(x,ε)=U(x,ε)+V(ξ,ε)+W(η,ε)+Z(t,ε),其中,U(x,ε)为外部展开,V(ξ,ε)和W(η,ε)为边界层校正项,Z(t,ε)为内部层展开式,

ξ为伸展变量.边界层和内部层项vj(ξ),wj(η)和zj(t)满足边界层函数性质

我们首先求解的外部展开式.当x≠x0时,考虑到脉冲源项当ε →0时的指数衰减性,原问题变为

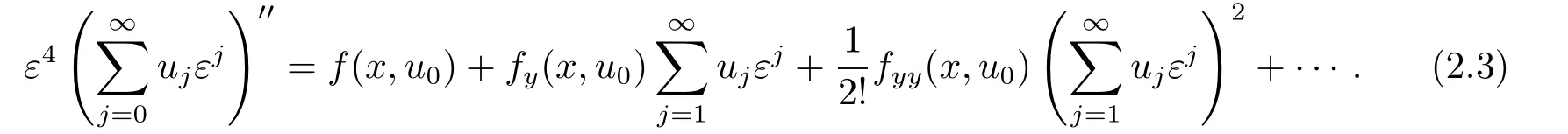
在(2.3)式中令ε →0 即得到退化方程f(x,u0) = 0,由假设(H)知它存在唯一光滑的解y=u0(x),x ∈[a,b].比较(2.3)式中ε1,ε2,ε3,ε4的系数,可得

类似地,u4k+1(x)=u4k+2(x)=u4k+3(x)≡0 (k=1,2,···),并可逐次确定u4k(k=2,3,4···).
为构造左边界层校正项,将y=U(x,ε)+V(ξ,ε)代入(2.1)式和(2.2)中的左边界条件y(a)=A,可得
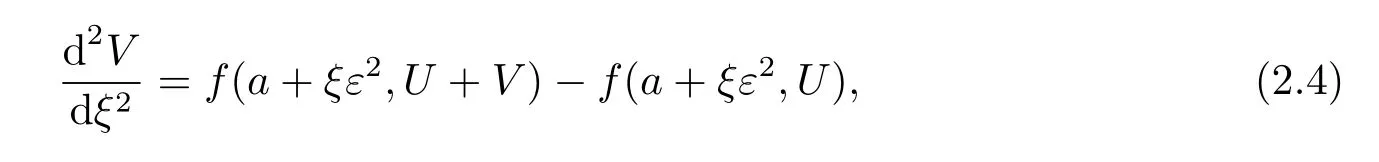

其中
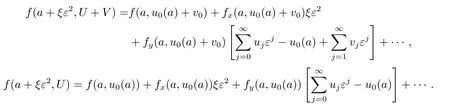
在式(2.4)-(2.5)中,令ε的同次幂系数相等,得到
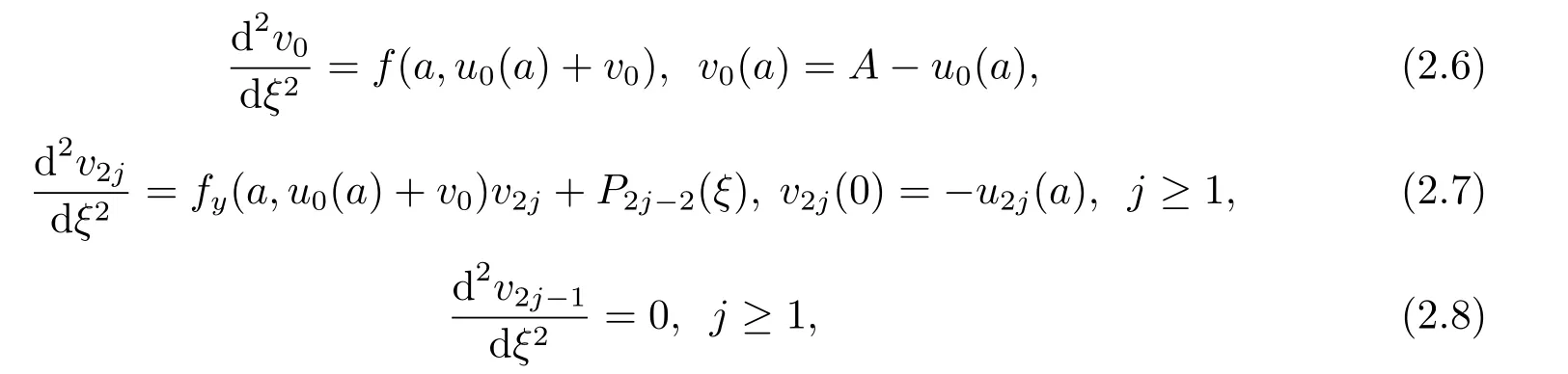
其中P2j−2(ξ)为由v0,v2,···v2j−2逐次确定的已知函数.

并且由假设(H)和文[2]中的定理2.2.3,可得v0(ξ) =O(exp(−ℓξ)),ξ →+∞.而式(2.7)中每个v2j(ξ)都可以用降阶法解出

其中ϕ(ξ)=−˙v0(ξ)为与(2.7)相应的齐次线性微分方程的解.
类似地,将y=U(x,ε)+W(η,ε) 代入(2.1)式和(2.2)中的右边界条件y(b) =B可逐次确定wj(η)(j=0,1,2,···),其中w0(η) 可以表示为

而

式中ψ(η)=−(η)满足齐次线性微分方程

Q2j−2(η)为在构造边界层函数时由w0,w2,···,w2j−2逐次确定的已知函数,并且每个wj(η)当η →+∞时是指数式衰减的.

其退化方程为

由假设(H)可知,它有唯一光滑的解y=φ(t).将y=U(x,ε)+Z(t,ε)代入(2.9)式有

其中

令方程(2.11)两边关于ε的同次幂系数相等,得到一系列递推代数方程,从而可逐次得到z0(t),z1(t),···.例如,z0(t),z1(t)满足代数方程

从(2.12)(2.13)可得

从前面外部解展开式的推导可知u1=0,u0(x) 满足代数方程f(x,u0(x))=0.
对上式两边关于x在x0处求导,可得

将u1=0和(2.14)代入(2.13),从而z1(t)可以表示为

命题1假设条件(H)成立,内部层校正项z0(t)和z1(t)有如下估计:
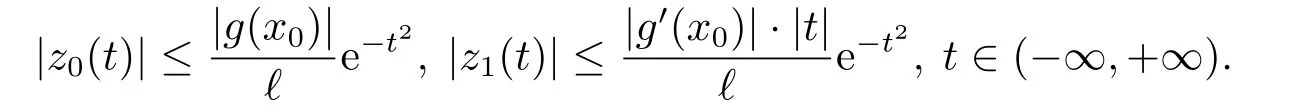
证注意到f(x0,u(x0))=0,由(2.10)式可得

从而从假设(H)知

关于z1(t)的估计可由(2.15)式利用假设(H)直接得到.证毕.
至此,我们得到原问题的一阶形式渐近解
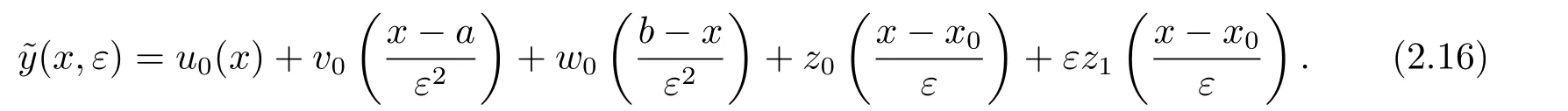
3 主要结论及证明
引理1[10](不等式理论) 假设函数α(x,ε),β(x,ε)∈C2[a,b] 使得
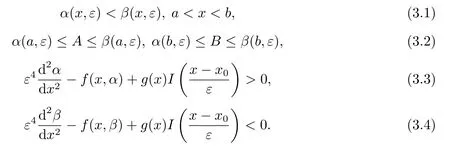
则边值问题(1.1)-(1.2)在区间[a,b]上存在一个解y=y(x,ε),且成立不等式

满足条件(3.1)-(3.4)的函数α(x,ε)和β(x,ε)分别称为问题(1.1)-(1.2)的一个下解和上解.
定理1假设(H)成立,则问题(1.1)-(1.2)在[a,b] 上存在一个解y(x,ε),且当ε →0 时满足

证选取界定函数

这里ξ,η,t为前面定义的伸展变量,r >0为待定常数.显然有,

为证明α(x,ε)满足式(3.3),将区间[a,b]分成三部分
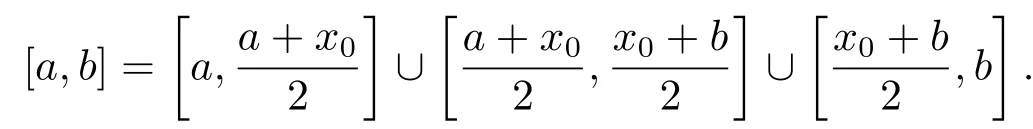

注意到渐近解的构造过程,可得


其中k >0 使得式(3.5)中|O(ε2)|≤kε2.

可如前类似证明


由(2.9)式知,
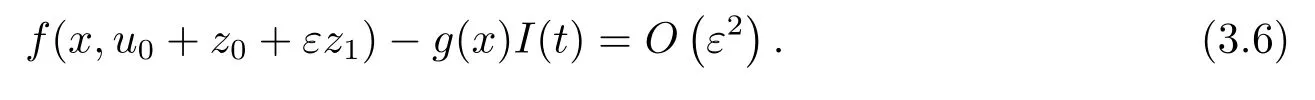
利用式(3.6),有

式中(x,•)=(x,u0+z0+εz1−θrε2),0<θ <1.

其中K >0,使得式(3.7)中|O(ε2)|≤Kε2.
这样我们证明了当r >max{k,K}时,α(x,ε)是问题(1.1)-(1.2)的一个下解.可完全类似可证β(x,ε)是问题(1.1)-(1.2)的一个上解.
显然,在[a,b]上,α(x,ε)≤β(x,ε).又因为每个当ε →0时为EST,故存在充分小的正数ε0,使得不等式α(a,ε)≤A ≤β(a,ε),α(b,ε)≤B ≤β(b,ε),对每个0<ε ≤ε0成立.根据引理,问题(1.1)-(1.2)在[a,b]上存在一个解y(x,ε),并且满足
α(x,ε)≤y(x,ε)≤β(x,ε),a ≤x ≤b.
4 例子
考虑两点边值问题

其退化问题的解为
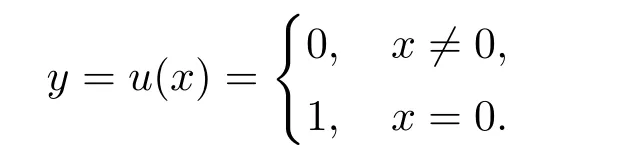
左右边界层v0(ξ),w0(η)分别满足

它们有精确解v0=e−ξ,w0=e−η.作尺度变换x=εt得到内部层项满足的方程

易求得内部层展开式的前两项为z0(t)=e−t2,z1(t)=0.
因此,从定理1知问题(4.1)-(4.2)的一阶渐近解为

进一步,从前面渐近解的构造过程我们也容易求出问题(4.1)-(4.2)的二阶渐近解

图1出示了当ε= 0.3时数值解与一阶渐近解和二阶渐近解的比较.二阶渐近解比一阶渐近数值解更好地吻合.当ε取更小值时,经典的数值方法将难以得到其数值解,此时渐近解将展示出巨大优势.

图1 当ε=0.3时数值解和一阶、二阶渐近解的比比较
- 应用数学的其它文章
- Fractional Integral Operators with Variable Kernels Associate to Variable Exponents
- 含凹凸非线性项的一般拟线性椭圆方程解的存在性
- Equilibrium Strategies of the Constant Retrial Queue with the N-Policy
- 基于Pena距离的偏正态数据下位置回归模型的统计诊断
- 带磁场的一维Schrdinger方程的逆散射问题
- The Group of Automorphisms of Total Orthogonal Graphs of Odd Characteristic

