基于Pena距离的偏正态数据下位置回归模型的统计诊断
聂兴锋,吴刘仓,邢伊琦
(昆明理工大学理学院,云南 昆明650093)
1.引言
在日常生活中,我们遇到的大多数数据并不具有严格的对称性,而具有一定的偏斜,如果此时再用正态分布等对称分布去描述它们的性质就有点不恰当了.目前,偏态数据的统计推断成为统计学研究的一个热点问题之一.
我们知道,统计诊断是数据分析的第一步,主要目的就是对样本数据中异常点或强影响点的识别和诊断.传统的判断异常点的常用统计量有Cook 距离、似然距离等.Pena[1]提出了一种度量线性回归模型影响的新的方法,这种方法与之前的方法有较大区别,之前的方法是研究删除一个(组)点对回归分析的影响以及对模型预测值的影响,或者是某个(组)样本点的微小扰动对参数估计的影响或是对模型预测的影响;而Pena距离这一统计量是研究样本中的某一点受其余各点的影响,也就是度量样本中各点删除后对某一特定点回归值以及预测值的影响.孟丽丽等[2]研究了基于Pena距离的加权最小二乘估计的影响分析;胡江等[3]−[5]研究了基于Pena距离的非线性回归模型和广义线性回归模型的影响分析.针对偏态数据的统计诊断方面,基于Cook距离、似然距离等,Xie等[6]研究了偏正态分布下非线性均值回归模型的统计诊断;万文等[7]研究了偏正态数据下联合位置与尺度模型的统计诊断.但是基于Pena距离的偏正态数据的统计诊断还没有人研究,而统计诊断又是数据分析必不可少的一部分.本文对Pena距离在偏正态数据下位置回归模型的影响分析进行了讨论,得出了比较有价值的相关结果.
2.偏正态分布下的位置回归模型
Ⅰ偏正态分布
1985年Azzalini[8]首次研究提出偏正态分布,若随机变量Y服从偏正态分布,即Y ∼SN(µ,σ2,λ) 其中µ表示位置参数,σ表示尺度参数,λ表示偏度参数.则其概率密度函数可表示为

其中φ(·),Φ(·)分别为标准正态分布的密度函数与分布函数.当偏度参数λ= 0 时,密度函数(2.1)退化为正态分布的密度函数,即此时偏正态分布退化为正态分布.

从E(Y)中我们可以看出µ只是均值的一部分.当λ≠ 0时,E(Y) =µ,此时分布不对称;当λ >0时,E(Y)>µ,此时分布右偏;当λ <0时,E(Y)<µ,此时分布左偏.所以,偏正态分布是正态分布的进一步推广.
Ⅱ偏正态分布下的位置回归模型
下面给出偏正态分布下的位置回归模型为:
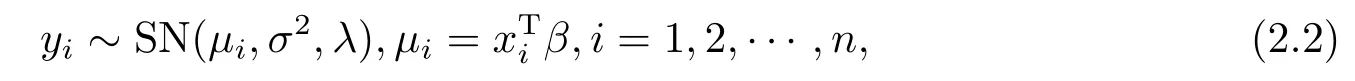
其中yi是被解释变量,服从位置参数为µ,尺度参数为σ,偏度参数为λ的偏正态分布,xi=(xi1,xi2,...,xip)T是与yi有关的解释变量.本文主要研究模型(2.2)的统计诊断方法.
ⅢPena距离
给定一组观测数据(xi,yi),i=1,...,n,yi为独立服从SN分布的随机变量,则位置回归模型(2.2)可表示为:

其中xi=(xi1,xi2,...,xip)T.其向量形式为:

其中Xi= (1,xi1,xi2,xi3,...,xip),X= (X1,X2,X3,...,Xn)为n×p的设计矩阵,维数为p,β为p×1的参数向量,ε为n×1的向量.则

其中(H=X(XTX)−1XT)是一个帽子矩阵,且有H2=H,HT=H.
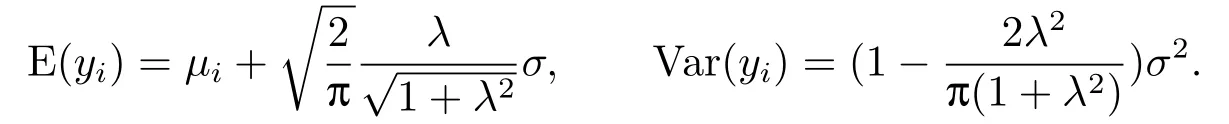
定理2.1模型(2.2)的Pena距离为:
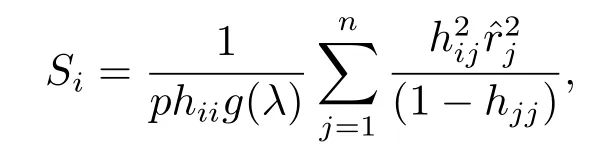
证根据文[1],我们定义Pena距离如下:其中由文[1]知:其中为第个i点的拟合值,是删除第j个点后第i个点的拟合值为帽子矩阵H的对角元素(杠杆值),p为帽子矩阵H的维数.所以有:
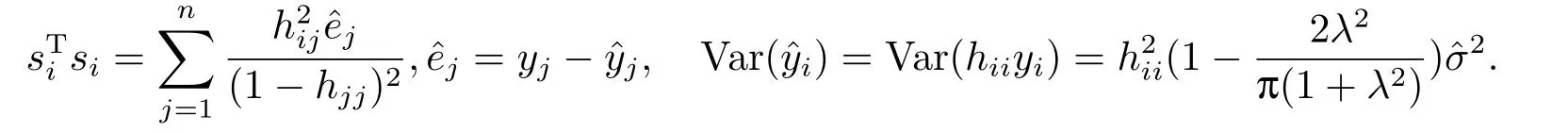
模型(2.2)对应的Pena距离如下:
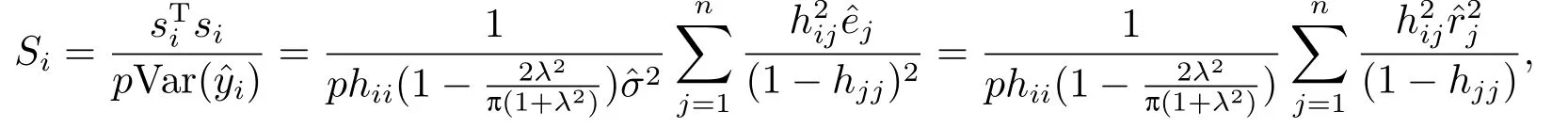
定理2.2当样本中不含有异常点时,有

证
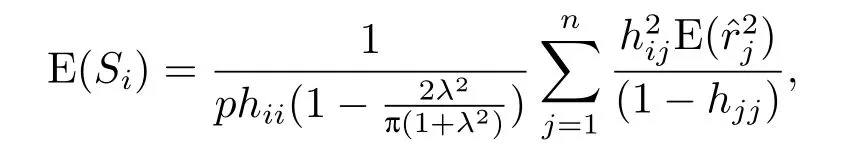
由韦博成等[9]可知: E(ˆr2j)=1,故


而当hjj ≥n1时,我们有
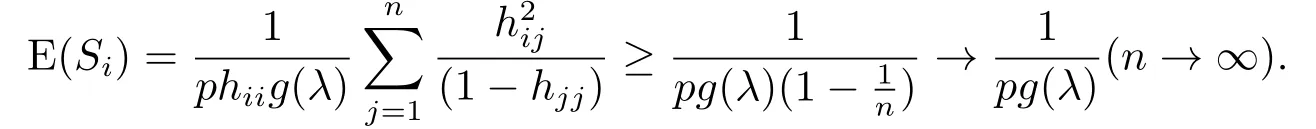
定理2.3当样本中含有高杠杆异常点时,统计量Si的期望,有
1) E(Si)→0,高杠杆异常点;
由定理2.3可知,当数据中含有一簇相同的高杠异常点时,可根据Si的值很容易找到它们但Cook 距离不能识别.特别,当λ=0时,g(0)=1,即可得到文[1-5]类似的结论.所以,本文进一步拓展了文[1-5]在偏态数据的实际应用.
3.偏正态数据下位置回归模型的统计诊断
Ⅰ数据删除模型
数据删除是统计诊断中最常用的方法之一,比较第i个点删除前后模型参数估计量之间的差异,能得出一些很好的结论.偏正态数据下位置回归模型的删除模型可表示为:

为检测第i个点是否为异常点或强影响点,可通过比较删除第i个点前后统计推断结果的变化,其中统计诊断量的变化可通过一些统计诊断量来刻画.
Ⅱ极大似然估计
对于模型(2.2),假设(yi,xi)为数据集中的第i个数据点,由模型(2.2)可知其密度函数为:
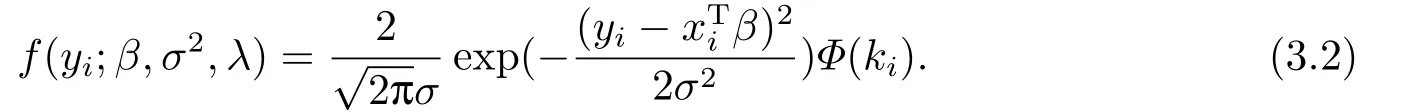
由(3.2)式可得似然函数为:
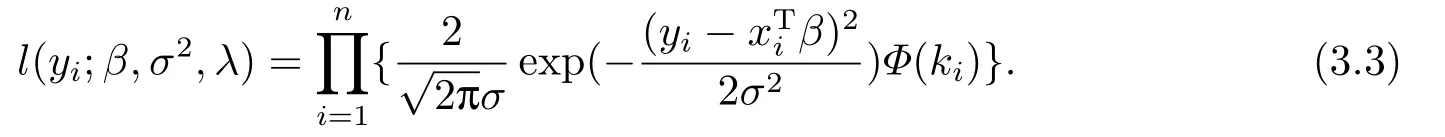
上式取自然对数,得其对数似然函数为:

令θ=(βT,σ2,λ)T,则L(β,σ2,λ)=L(θ).因此

利用Gauss-Newton迭代法[10]可得到参数极大似然估计的估计值.设未删除模型的参数估计值用表示删除模型的参数估计值则可以用表示,即删除第i个点后的参数估计值则表示删除第j个数据点后第i个数据点的参数估计值.
Ⅲ基于数据删除模型的诊断统计量
i) 似然距离及其计算
在数据删除模型框架下,似然距离是与Cook距离同等重要的诊断统计量.由于似然距离的定义并不限于线性模型,故而可以用于相当广泛的统计模型,诸如非线性模型、广义线性模型等.针对本文中的删除模型(3.1),第i个点的似然距离定义为:

由于L()为全局最优解,因此LDi ≥0恒成立.似然距离反应了第i个数据点(xi,yi)对参数θ的极大似然估计的影响.对于远大于其似然距离的点,则为异常点或强影响点.由于似然距离没有显示解,因此需要用近似计算得出其数值解.对(3.5)式在处进行泰勒展开可得:
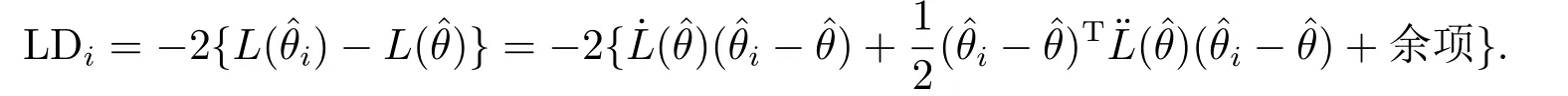

其中I()为Fisher信息阵,为方便计算,本文使用Fisher观测阵计算似然距离LD∗i.
ii) Cook距离及其计算
Cook距离是当今统计诊断中最重要的诊断统计量之一.针对本文中的删除模型(3.1),第i个点的Cook距离定义如下:其中H=X(XTX)−1XT为帽子矩阵,p为对应解释变量的维数,ˆσ2为未删除模型方差的估计值.具体分析时,先计算出各点的Cook距离,通过画散点图,找出其中特别大的,对应的数据点可能就是异常点或强影响点.
iii) Pena距离及其计算
Cook距离研究的是删除一个(组)点后对估计值或预测值的影响,而Pena距离则研究的是样本中的某一点受其余各点的影响,简单来说,就是样本中各点删除后,对某一特定的点的估计值或预测值的影响,Pena距离定义如下:其中H=X(XTX)−1XT为帽子矩阵,p为对应解释变量的维数,为删除第i个点后模型方差的估计值.则表示删除第j个数据点后第i个数据点的参数估计值.具体分析时,同样是先算出删除各点后某一点的Si,画出散点图,Si较大的则可能是异常点或强影响点.
4.Monte Carlo模拟
为了比较Pena距离与Cook距离、似然距离的诊断效果,根据模型(2.2),产生偏正态数据,其中xi ∼U(−1,1),取β=(1,1,1),σ=2,λ=0.5.将第20 号,80 号,180号样本点的被解释变量的值做改变,即从样本点中制造3个异常点,然后应用本文研究的方法如似然距离,Cook距离和Pena距离进行诊断.根据这3个异常点的诊断情况来判断本文提出的方法是否行之有效.模拟结果如图1,图2和图3所示,其中图1为样本量为200时模拟数据的似然距离LD散点图,图2样本量为200时模拟数据的Cook距离散点图,图3样本量为200时模拟数据的Pena距离散点图.

图1 样本量为200时模拟数据的LD散点图
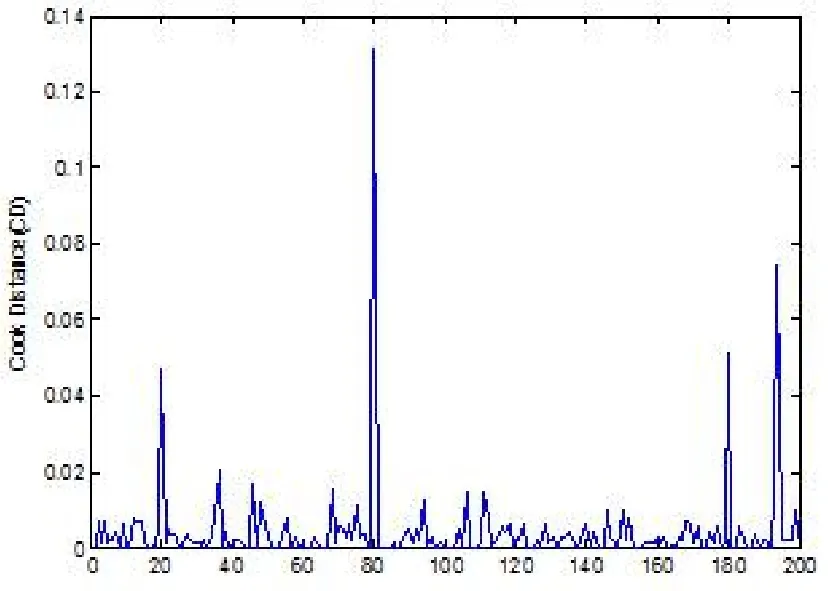
图2 样本量为200时模拟数据的CD散点图

图3 样本量为200时模拟数据的PD散点图
从图中我们可以很清晰的看出,第20,80,180号异常点均被诊断出来了,表明我们的方法是行之有效的,下面用实例进一步说明具体的应用.
5.实例分析
Ⅰ发动机性能数据[11]
如下表1所示是一组检验某种工业用发电机性能试验的数据,该试验使用的原料是柴油和从有机原料中通过蒸馏产生的气体的混合物,在各种不同的速度x(计量单位:百转/分钟)下,测量发动机的马力y.
用QQ图对发动机的马力y数据进行正态性检验,结果如图4所示,表明数据具有一定的偏斜.利用MATLAB中的偏度函数skewness(),峰度函数kurtosis()得到发动机的马力y的偏度为-0.3332,峰度为1.9679,而正态分布的偏度值为0,峰度值为3.综合分析可知,发动机性能数据服从偏态分布,可用本文研究的方法进行统计诊断.
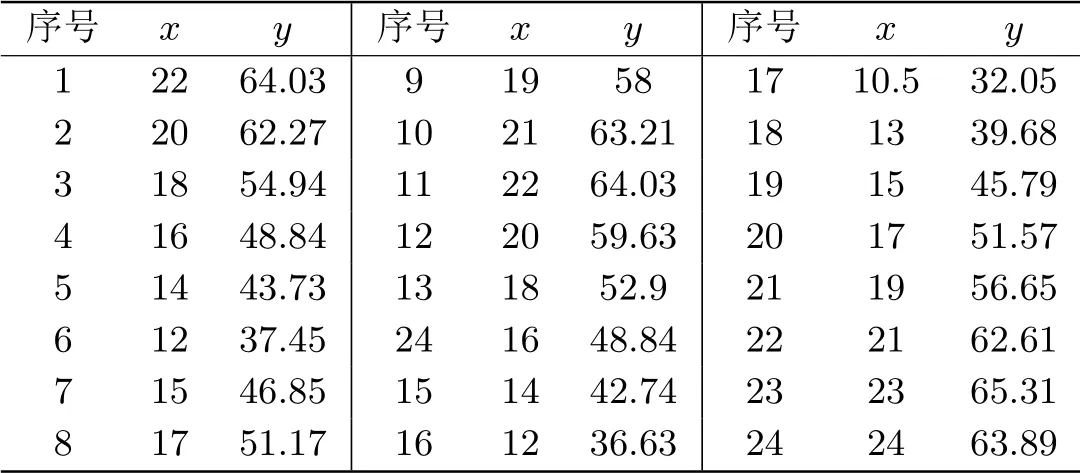
表1 发动机性能数据
本文考虑发动机的马力y与在各种不同的速度x(计量单位:百转/分钟)的位置回归模型.经过计算得到完全数据下模型(2.2)的参数估计结果如下:

由图5可知第2,10,17,24号点可能为异常点或强影响点,由图6可知第2,10,24号点可能为异常点或强影响点,由图7可知第2,24号点可能为强影响点或异常点.由韦博成等[9]的例5.4可知第2,24号点为异常点或强影响点.比起似然距离和Cook距离,Pena距离很好的诊断出了这两个点.
Ⅱ红鳟鲑鱼数据[12]
鱼卵数量x当年可捕捞的成鱼数量y之间的关系,是经营渔场者十分关心的问题.下表2所示是1940年至1967年在Skeener河中红鳟鲑鱼的产卵量x和可捕捞的成鱼量y的测量数据.

表2 红鳟鲑鱼数据

图4 发动机性能数据的正态性检验QQ图
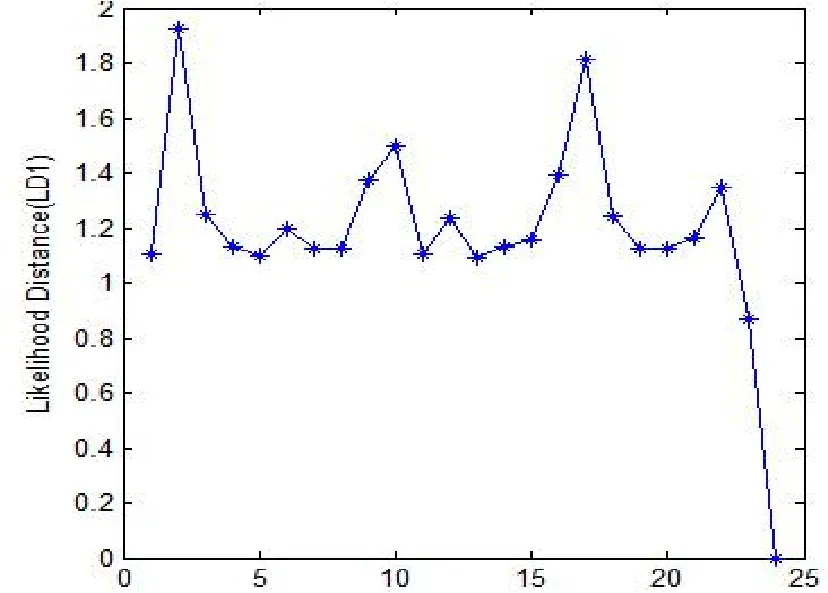
图5 发动机性能数据似然距离LD散点图
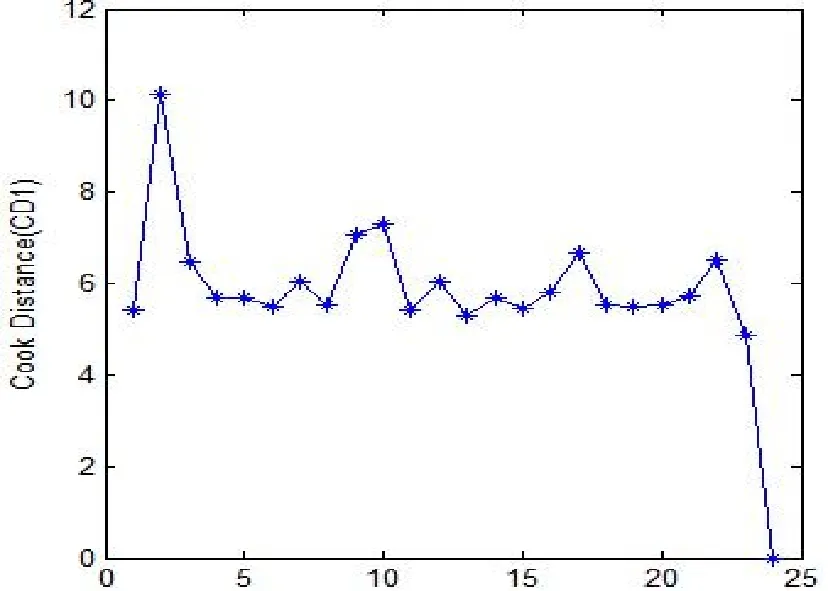
图6 发动机性能数据Cook距离CD散点图

图7 发动机性能数据Pena距离PD散点图
利用MATLAB中的偏度函数skewness()、峰度函数kurtosis()得到红鳟鲑鱼当年可捕捞的成鱼数量y的偏度为0.7063,峰度为3.0568,而正态分布的偏度值为0,峰度值为3.综合分析可知,红鳟鲑鱼当年可捕捞的成鱼数量y服从偏态分布.我们分别用正态分布下的Pena距离和偏正态分布下的Pena距离诊断做比较,比较结果如图8,图9所示.

图8 正态分布下的Pena距离散点图

图9 偏正态分布下的Pena距离散点图
从图8我们可以看出第5号点为异常点或强影响点,而从图9可以看出第5,12号点为异常点或强影响点.由文[9]中例6.4可知第5,12号点为异常点或强影响点,这是合理的,因为在原始数据中,第5,12 号点分别是被解释变量的最大值点和最小值点.偏正态分布下的Pena距离很好的诊断出了这两个点,而正态分布下的Pena 距离则只诊断出了一个点.相比较而言,偏正态分布下的Pena距离诊断效果比正态分布下的Pena 距离要好.
- 应用数学的其它文章
- Fractional Integral Operators with Variable Kernels Associate to Variable Exponents
- 含凹凸非线性项的一般拟线性椭圆方程解的存在性
- 具有脉冲源项的二阶半线性奇摄动边值问题
- Equilibrium Strategies of the Constant Retrial Queue with the N-Policy
- 带磁场的一维Schrdinger方程的逆散射问题
- The Group of Automorphisms of Total Orthogonal Graphs of Odd Characteristic

